第七章学习小结
查找的基本概念:
查找表:同一类型的数据元素(记录)构成的集合。
静态查找表:对查找表只进行查找操作。动态查找表:不仅进行查找操作,而且在查找过程中还伴随着插入(查找的数据元素不在表中时)、删除某个数据元素的操作。
关键字(key):是数据元素(或记录)的某个数据项的值,用它可标识(识别)一个数据元素(或记录)。
平均查找长度(ASL):需和给定值进行比较的关键字个数的期望。
ASL=∑i=1nPiCi
ASL=∑i=1nPiCi
n:表中记录个数
PiPi:查找第i个记录的概率
CiCi:找到第i个记录需要进行的对比次数。
以下这张图是一位大佬博客(https://blog.csdn.net/qq_25508039/article/details/76011228)的知识框图:
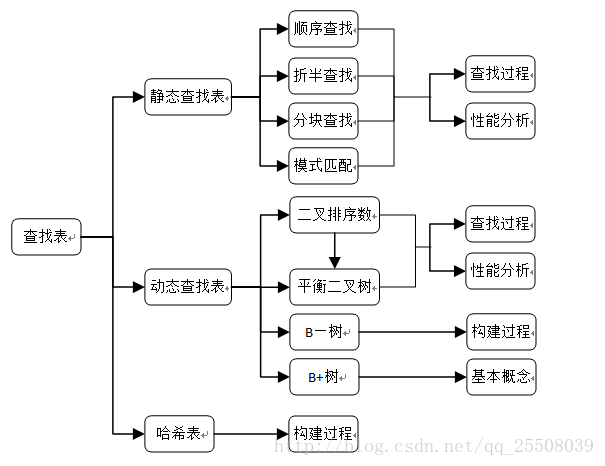
书上也总结了顺序查找、折半查找和分块查找的比较:
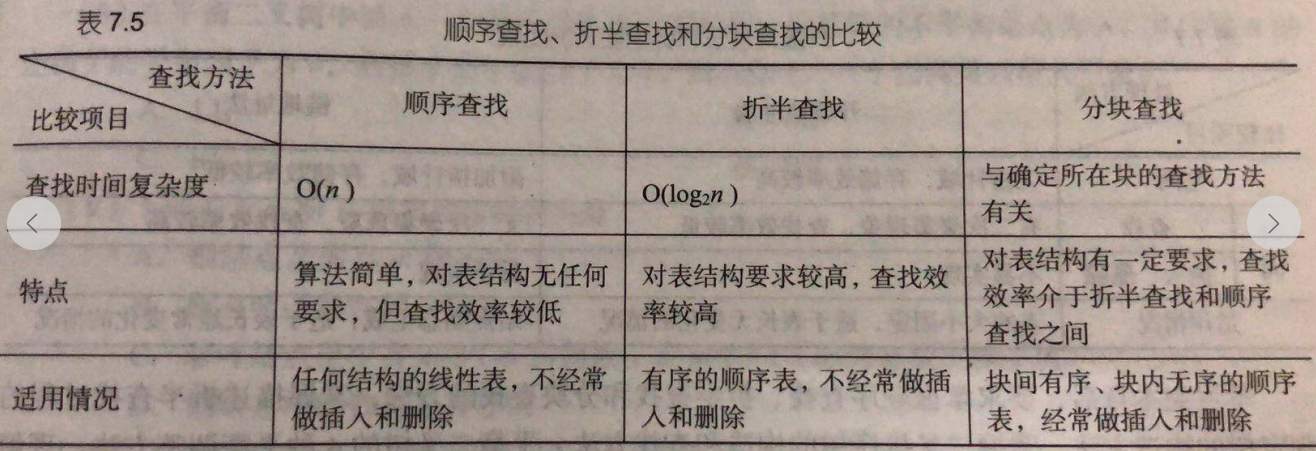
折半查找和二叉树查找的比较:
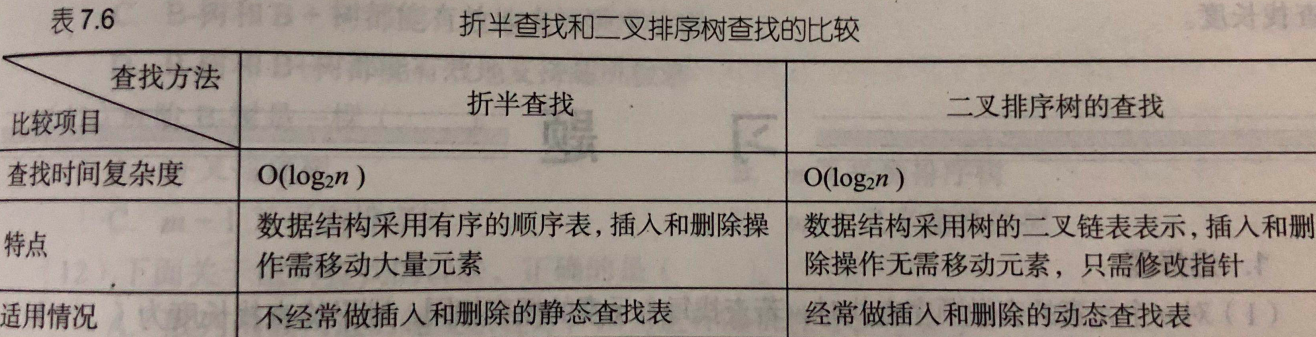
B树
即二叉搜索树:
1.所有非叶子结点至多拥有两个儿子(Left和Right);
2.所有结点存储一个关键字;
3.非叶子结点的左指针指向小于其关键字的子树,右指针指向大于其关键字的子树;
B树的搜索,从根结点开始,如果查询的关键字与结点的关键字相等,那么就命中;否则,如果查询关键字比结点关键字小,就进入左儿子;如果比结点关键字大,就进入右儿子;如果左儿子或右儿子的指针为空,则报告找不到相应的关键字;
如果B树的所有非叶子结点的左右子树的结点数目均保持差不多(平衡),那么B树的搜索性能逼近二分查找;但它比连续内存空间的二分查找的优点是,改变B树结构(插入与删除结点)不需要移动大段的内存数据,甚至通常是常数开销;
B-树
B-tree,即B树,而不要读成B减树,它是一种多路搜索树(并不是二叉的):
1.定义任意非叶子结点最多只有M个儿子;且M>2;
2.根结点的儿子数为[2, M];
3.除根结点以外的非叶子结点的儿子数为[M/2, M];
4.每个结点存放至少M/2-1(取上整)和至多M-1个关键字;(至少2个关键字)
5.非叶子结点的关键字个数=指向儿子的指针个数-1;
6.非叶子结点的关键字:K[1], K[2], …, K[M-1];且K[i] < K[i+1];
7.非叶子结点的指针:P[1], P[2], …, P[M];其中P[1]指向关键字小于K[1]的子树,P[M]指向关键字大于K[M-1]的子树,其它P[i]指向关键字属于(K[i-1], K[i])的子树;
8.所有叶子结点位于同一层;
B-树的特性:
1.关键字集合分布在整颗树中;
2.任何一个关键字出现且只出现在一个结点中;
3.搜索有可能在非叶子结点结束;
4.其搜索性能等价于在关键字全集内做一次二分查找;
5.自动层次控制;
B+树
B+树是B-树的变体,也是一种多路搜索树:
1.其定义基本与B-树同,除了:
2.非叶子结点的子树指针与关键字个数相同;
3.非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树(B-树是开区间);
5.为所有叶子结点增加一个链指针;
6.所有关键字都在叶子结点出现;
B+的特性:
1.所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好是有序的;
2.不可能在非叶子结点命中;
3.非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层;
4.更适合文件索引系统;
原因: (2)增删文件(节点)时,效率更高,因为B+树的叶子节点包含所有关键字,并以有序的链表结构存储,这样可很好提高增删效率。
而散列表的查找主要是如何构造散列函数和如何处理冲突。
如何构造散列函数:
1、数字分析法
2、平方取中法
3、折叠法
处理冲突的方法
1、开放地址法
2、链地址法
以下为开放地址和链地址之间的比较
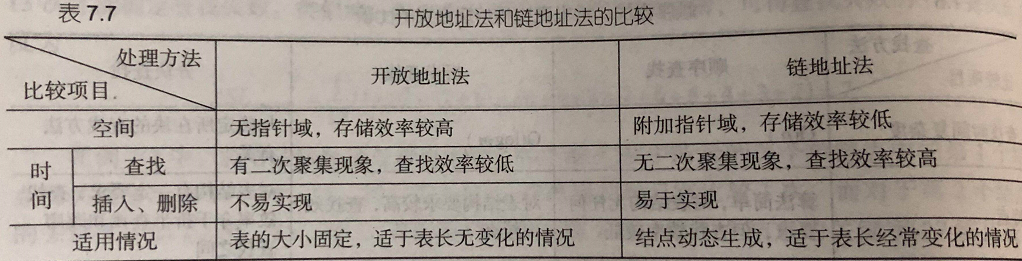
二叉排序树
二叉排序树的插入算法:
struct BiTree {
int data;
BiTree *lchild;
BiTree *rchild;
};
//在二叉排序树中插入查找关键字key
BiTree* InsertBST(BiTree *t,int key)
{
if (t == NULL)
{
t = new BiTree();
t->lchild = t->rchild = NULL;
t->data = key;
return t;
}
if (key < t->data)
t->lchild = InsertBST(t->lchild, key);
else
t->rchild = InsertBST(t->rchild, key);
return t;
}
//n个数据在数组d中,tree为二叉排序树根
BiTree* CreateBiTree(BiTree *tree, int d[], int n)
{
for (int i = 0; i < n; i++)
tree = InsertBST(tree, d[i]);
}
二叉排序树的删除算法:
#define Status bool
Status Delete(BiTree*);//必须先声明
Status DeleteBST(BiTree &TParent,BiTree &T, KeyType key)//若二叉排序树T中存在关键字等于key的数据元素时,则删除该数据
//元素,并返回TRUE;否则返回FALSE
{
if(!T)//不存在关键字等于key的数据元素
return false;
else
{
if(key == T->data.key)//找到关键字等于key的数据元素
return Delete(Parent_T, T);
else if(key < T->data.key)
return DeleteBST(T, T->lchild,key);
else
return DeleteBST(T, T->rchild,key);
}
return true;
}
Status Delete(BiTree& fp , BiTree&p)//从二叉排序树中删除结点p,并重接它的左或右子树
{
if(!p->rchild)//右子树空则只需重接它的左子树
{
fp->lchild = p->lchild;
delete(p);
}
else if(!p->lchild)//左子树空只需重接它的右子树
{
fp->rchild = p->rchild;
delete(p);
}
else//左右子树均不空
{
q=p;
fp->lchild = p->lchild;
s=p->lchild;//转左
while(s->rchild)//然后向右到尽头
{
q=s;
s=s->rchild;
} //此时q是s的父结点
s->rchild=p->rchild; //将s的左子树作为q的右子树
delete(p);
}
return true;
}






