特殊数列（长期项目）

前排提醒： $\LaTeX$ 可能过多，请耐心等待加载

斐波那契数列（Fibonacci）#

可能不是很特殊，但是确是最为常见的，看名字就知道明显是个叫做斐波那契的人发现的，全名 莱昂纳多·斐波那契（Leonardo Fibonacci）（意大利）。

• 定义： $f_0 = 0, f_1 = 1, f_n = f_{n - 1} +f_{n-2}(n \geq 2)$

  生成函数 $F(x)=\dfrac{1}{1-x-x^2}$

• 通项公式： $f_n = \dfrac{1}{\sqrt 5}[(\dfrac{1+\sqrt5}{2})^n - (\dfrac{1-\sqrt 5}{2})^n]$，推导方式有很多种，这里使用最简单的两种

  • 特征方程法：(都是自己盲猜的，有误请指正)

    数列中特征方程法本质上就是构造等比数列，只不过完全看不出来（瞎猜）

    $$f_n =f_{n-1}+f_{n-2} \iff f_n-f_{n-1}-f_{n-2}=0$$

    可以看出 $f_n、f_{n-1}、f_{n-2}$ 形式一样，我们设其为 $f_n=aq^n$，则

    $$\begin{aligned} &aq^{n+2}-aq^{n+1}-aq^n=0 \\ \iff &aq^n(q^2-q-1)=0 \\ \iff &aq^n(q-\dfrac{1+\sqrt5}{2})(q-\dfrac{1+\sqrt5}{2})=0 \\ 有\ &f_{1,n} = a(\dfrac{1+\sqrt5}{2})^n, f_{2,n}=a(\dfrac{1-\sqrt5}{2})^n \\ 将特解线性组合得通解\ &f_n = Af_{1,n} +Bf_{2,n} \end{aligned}$$

    将 $f_0 =0,f_1 =1$ 代入：

    $$\begin{aligned} &\begin{cases} Aa+Ba=0 &(1)\\ Aa\left(\dfrac{1+\sqrt5}{2}\right)+Ba\left(\dfrac{1-\sqrt5}{2}\right)=1&(2) \end{cases} \\ \\ 解(1):&\ a(A+B)=0 \\ &\because a \not= 0（等比数列性质）\\ &\therefore A+B=0 \iff B=-A \\ 代入(2):&Aa\left(\dfrac{1+\sqrt5}{2}-\dfrac{1-\sqrt5}{2}\right)=\sqrt5Aa=1 \\ & \iff Aa=\dfrac{1}{\sqrt5} \end{aligned}$$

    再将两个结论代入原数列：

    $$\begin{aligned} f_n = \ &Aa(\dfrac{1+\sqrt5}{2})^n+Ba(\dfrac{1-\sqrt5}{2})^n \\ =\ & Aa[(\dfrac{1+\sqrt5}{2})^n-(\dfrac{1-\sqrt5}{2})^n] \\ =\ & \dfrac{1}{\sqrt5}\left[\left(\dfrac{1+\sqrt5}{2}\right)^n-\left(\dfrac{1-\sqrt5}{2}\right)^n\right] \end{aligned}$$

  • 生成函数法：

    $f_n$的普通型生成函数为 $F(x)$，则 $F(x) = x+x^2+2x^3+3x^4+5x^5+...+f_n x^n+...$

    利用无穷项的特性，显然有 $F-Fx=Fx^2+x \iff F=\dfrac{x}{1-x-x^2}$

    然后因式分解、裂项：

    $$\begin{aligned} F(x) &= \dfrac{x}{1-x-x^2} = \dfrac{x}{(1-\phi_1x)(1-\phi_2x)} ,解得 \phi_1=\dfrac{1+\sqrt5}{2}, \phi_2=\dfrac{1-\sqrt5}{2}\\ &=x(\dfrac{a}{1-\phi_1x}+\dfrac{b}{1-\phi_2x})=x(\dfrac{a+b-x(a\phi_2+b\phi_1)}{(1-\phi_1x)(1-\phi_2x)}) \\ \iff &\begin{cases} a+b=1\\a\phi_2+b\phi_1=0\end{cases}, 解得\begin{cases} a=\dfrac{5+\sqrt5}{10}=\dfrac{1}{\sqrt5}\cdot\dfrac{\sqrt5+1}{2}\\ b=\dfrac{5-\sqrt5}{10}=\dfrac{1}{\sqrt5}\cdot\dfrac{\sqrt5-1}{2} \end{cases} \\ \iff F(x) &=ax\dfrac{1}{1-\phi_1x}+bx\dfrac{1}{1-\phi_2x} \\ &=ax(1+\phi_1x+\phi_1^2x^2+...+\phi_1^nx^n+...)+bx(1+\phi_2x+\phi_2^2x^2+...+\phi_2^nx^n+...) \\ &=\dfrac{1}{\sqrt5}(\dfrac{1+\sqrt5}{2}x+(\dfrac{1+\sqrt5}{2})^2x^2+...+(\dfrac{1+\sqrt5}{2})^nx^n+...) \\ &-\dfrac{1}{\sqrt5}(\dfrac{1-\sqrt5}{2}x+(\dfrac{1-\sqrt5}{2})^2x^2+...+(\dfrac{1-\sqrt5}{2})^nx^n+...) \end{aligned}$$

    据此，我们很容易看出 $f_n = \dfrac{1}{\sqrt5}\left[\left(\dfrac{1+\sqrt5}{2}\right)^n-\left(\dfrac{1-\sqrt5}{2}\right)^n\right]$

• 一些性质：

  • 与黄金分割比的关系：

    $$\large \lim_{n\rightarrow\infty} \dfrac{f_{n-1}}{f_{n}} = \dfrac{\sqrt5-1}{2}$$

    $\rm{Proof:}$

    $f_n=f_{n-1}+f_{n-2} \iff \dfrac{f_n}{f_{n-1}}=1+\dfrac{f_{n-2}}{f_{n-1}}$，设极限 $\lim_{n\rightarrow\infty}\dfrac{f_n}{f_{n-1}}$存在且为 $x$。

    则 $\lim_{n\rightarrow\infty}\dfrac{f_{n-2}}{f_{n-1}}=\lim_{n\rightarrow\infty}\dfrac{f_{n-1}}{f_{n}}=\dfrac{1}{x}$，故：

    $$x=1+\dfrac{1}{x} (x>1)$$

    解得 $x=\dfrac{1+\sqrt5}{2} \iff \lim_{n\rightarrow\infty}\dfrac{f_{n-1}}{f_{n}} = \dfrac{1}{x}=\dfrac{\sqrt5-1}{2}$

  • 1. 平方项与前后项（勾股特征）：
       $$\large f_n^2-f_{n-1}f_{n+1}=(-1)^{n-1} \\ \large \iff \left|f_n^2-f_{n-1}f_{n+1}\right| = 1（定值）$$

2. 求和：

$$\large \begin{aligned} 全项：&\sum_{i=0}^n f_i=f_{n + 2} \\ 奇项：&\sum_{i=1}^nf_{2i-1}=f_{2n} \\ 偶项：&\sum_{i=1}^nf_{2i}=f_{2n+1}-1 \\ 平方项：&\sum_{i=1}^n f_n^2=f_nf_{n+1} \end{aligned}$$

3. 两倍项关系：

$$\large\dfrac{f_{2n}}{f_n}=f_{n-1}+f_{n+1}$$

4. 隔项关系：

   $$\large f_{2n-2m-2}(f_{2n}+f_{2n+2})=f_{2m+2}+f_{4n-2m}, \ \ \ \ (n > m \geq -1, n \geq 1)$$

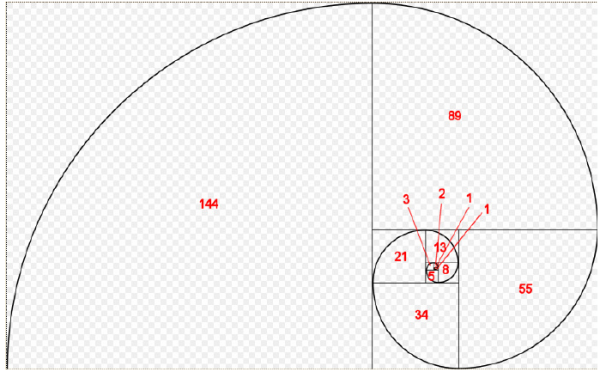
   5. 将杨辉三角左对齐，所有斜率为 1 的直线上数的和为 f 的某一项

      $$\large f_n = \sum_{i=0}^m \binom{n-1-i}{i}$$

      其中 m 为同一直线上数的个数。事实上这个结论是那样的显然，以至于写出来有点累赘了

   6. $$\large {m|n\implies f_m | f_n \\ f_{(n,m)}=(f_n, f_m)}$$

• 因为我觉得这个线看起来很和谐，所以就搬上来了/xyx：

  

  该图很好地证明了平方项求和的结论：$\large \sum_{i=0}^nf_i^2=f_n f_{n+1}$

• 生成函数： 没啥好说的，普通生成函数 $F(x)=\dfrac{x}{1-x-x^2}=x+x^2+2x^3+3x^4+...+f_{\infty}x^{\infty}$

• 矩阵递推： $\begin{bmatrix}f_{n}&f_{n+1}\end{bmatrix}=\begin{bmatrix}f_{n-1}&f_n\end{bmatrix} \times \begin{bmatrix}0&1\\1&1\end{bmatrix}$ ，可以快速得求出第 n 项。

• 推广：

  • 斐波那契-卢卡斯数列：

    卢卡斯数列： 1, 3, 4, 7, 11, 18...， （斐波那契—卢卡斯递推：$a_n=a_{n-1}+a_{n-2}(n\geq 2)$），简而言之，初值 $a_0、a_1$不同。

    以 a、b 为前两项的、满足斐波那契—卢卡斯递推的数列 $F(a,b)$ 就是斐波那契-卢卡斯数列。其所有数列都满足勾股特征( $\left|f_n^2-f_{n-1}f_{n+1}\right|$ 为定值)，但不一定满足 $\left|f_n^2-f_{n-1}f_{n+1}\right|=1$（自然特征）

  • 广义斐波那契数列：

    递推式诸如 $f_n = pf_{n-1}+qf_{n-2}$ 的数列称为广义斐波那契数列。

    啊这我怎么感觉好多好多常见数列都是广义斐波那契数列（自然数、等差、等比……）

---

错位排列#

• 定义： 最早起源于信封问题，现在可以看成：满足任意 $a_i \not= i$ 的排列数（瞎扯）

  这显然只与 n 有关，设 $d_n$ 为 n 个数字错位排列的方案数，则有：

$$n!=\sum_{i=0}^n \binom{n}{i} d_i$$

​ 其意义为：n 个数的全排列为 1~n 位全错位排列重新排列（i 个全错位重新分配到 n 个数中）的方案数之和。
​

​ 容易发现 $\binom{n}{i}d_i$ 为 n-i 位不错排，i 位为错排的方案数，求和即为全排列。

• 推导公式及化简：

  • 将 (1) 式二项式反演，有通项公式：

    $$\begin{aligned} d_n &= \sum_{i=0}^n (-1)^i \binom{n}{i}(n-i)! \\ &= \sum_{i=0}^n (-1)^i \dfrac{n!}{(n-i)!i!} (n-i)! \\ &= n!\sum_{i=0}^n \dfrac{(-1)^i}{i!} \end{aligned}$$

    这个结论同样可以暴力容斥得到，但其实二项式反演的本质即容斥：

    $$d_n = \sum_{S \in [n]} (-1)^{|S|} (n-|S|)!$$

    同样可以推出上面的通项公式。

    这对于手算来说还是太繁琐了，有更简便的计算吗？

    注意到 $e^x$ 的 Taylor 展开式为 $\displaystyle\sum_{i=0}^\infty \frac{x^i}{i!}$，当代入 $x = -1$ 时，有 $e^{-1} = \displaystyle\sum_{i=0}^\infty \frac{(-1)^i}{i!}$，与我们获得的通项公式中的某一项十分相似。

    当 n 很大的时候，可以近似得认为$e^{-1} = \displaystyle\sum_{i=0}^n \frac{(-1)^i}{i!}$ ，代入通项公式得近似公式：

    $$d_n \approx \dfrac{n!}{e}$$

    经过误差考量我们发现，误差最大时将其值四舍五入即可得到正确答案，而误差随 $n \rightarrow \infty$ 而逐渐减小，故有更简便的计算公式：

    $$d_n =\left \lfloor \dfrac{n!}{e} +\dfrac{1}{2} \right \rfloor$$

    而这同时也说明了在 n 越来越大的时候，全排列数与错排数的比值趋近自然底数 e，真是美妙。

  • 递推公式：

    $$d_n = (n - 1) (d_{n - 1} + d_{n - 2})$$

    感性理解，放入第 n 个数字时：

    • 如果前面 n - 1 个数已是全错位排列，随便与一个数交换，也能得到一个错位排列。

    • 如果存在某个数不是错排（n - 2 位全错排），则必须与之交换，否则无法构成全错位。

    这式子与前两项都有关，我们尝试化简：

    $$\begin{aligned} &d_n = (n-1)d_{n-1} + (n-1)d_{n-2} \\ \iff & d_n - nd_{n-1} = -(d_{n- 1} - (n-1)d_{n-2}) \end{aligned}$$

    设 $c_n = d_n - nd_{n-1}$, 则 $c_2 = d_2 = 1$，易得 $c_n = 1\times(-1)^{n-2} = (-1)^n$
    得递推公式：

    $$\displaystyle{d_n = nd_{n-1} + (-1)^n}$$

• 生成函数： 指数型生成函数 $\hat{D(x)} = \dfrac{1}{e^x(1-x)}$

  之前已经讨论过 Bell数列生成函数的推导 ，但在 H 队博客里还提到了这么一个结论：

  因此，我们可以归纳出 exp 函数在生成函数运算上的组合意义：设有标号组合对象 A 的指数型生成函数为 $\hat{A(x)}$，表 $[x^n]\hat{A(x)}\times n!$ 示组合 n 个元素的方案数，那么 $\hat{B(x)}=e^{\hat{A(x)}}$ 就是把元素划分为若干无标号不交并，每一个子集内当作组合对象 A 来处理，所对应的 EGF（指数型生成函数）.

  错位排列一定是由一些大小不为 1 的置换环组合而来，比如 $\text{2 3 4 5 6 1}$ 是一个大小为 6 的置换环，而 $\text{2 3 1 5 6 4}$ 则是两个大小为 3 的置换环组合来的。错排的定义正好吻合：不存在大小为 1 的置换环。

  每个置换环可以看作单独的一个对象 A，而 $\hat{A(x)}$ 即为环排列的生成函数 $\hat{G} -x= \ln\dfrac{1}{1-x}-x$（减去大小为 1 的置换环）

  则错位排列的生成函数即为：

  $$\hat{D(x)} = e^{\hat{A(x)}} = e^{\ln \frac{1}{1-x}-x} = \dfrac{1}{(1-x)e^x}$$

  泰勒展开验算：

  $$1 + \dfrac{x^2}{2!} + \dfrac{2x^3}{3!} + \dfrac{9x^4}{4!} + \dfrac{44 x^5}{5!} + ...$$

  系数就是错排数。

• 拓展应用：

  • 上面那个容斥的通项计算可以推广到一些特殊形式：m 个点已经给定的错排数，或 n-k 错排（理论）

  我们考虑给定了 m 个点的错排数，需要我们填的只有 n-m 个空，类似于之前容斥：

  $$ans = \sum_{i=0}^{n-m} (-1)^{i}\binom{n-m}{i} (n-m-i)!$$
  • 1. 对于 n 个数中选 m 个构成错排的方案数，一种比较直观的方法是算出所有存在非错排的方案数：
    $$ans = \sum_{i=\max(2m-n,0)}^m \binom{m}{i}\binom{n-i}{m-i}\sum_{0\le j \le i}(-1)^j\binom{i}{j}(m-j)!$$

    其含义为选出的 m 个数字中有 i 个在 $[1,m]$ 的范围内，那么选出 i 个可能在自己位置上，方案数 $\binom{m}{i}$ ；其余有 $m-i$ 个位置，随便在剩下的 $n - i$ 个数字中选即可，方案数 $\binom{n-i}{m-i}$ 接下来考虑这每一种构成非错排的不重不漏的方案数，套用错排计算通项即可。

    2. 对于只有一重和式的做法，可以考虑这么一种构造：一个 n 的任意排列，选前 m 个有效位，构成错排的方案数；除去 n!，也就是所有方案数。除去每次重复的 $(n-m)!$ 就可以计算出总方案数。
       $$\displaystyle \sum_{i=1}^m (-1)^{i-1} \binom{m}{i}(n-i-m)!$$

    在前 m 位中选 i 个位错排，剩下全随便选，容斥一下可得方案数。

卡特兰数（Catalan number）#

• 定义：是组合数学中一个常出现于各种计数问题中的数列。百度百科上就是这么定义的。

  前几项（0开始）：1,1,2,5,14,42,132,429,1430,4862,16796...，

  其中第 i 项记为$c_i$。

  我们主要研究卡特兰数的诸多实际应用，如合法出栈序列、合法括号匹配、多边形划分、二叉树形态等。

• 生成函数： 指数型生成函数 $C(x)=\dfrac{1-\sqrt{1-4x}}{2x}$

  Proof:

  $$\begin{split} &C(x)= \sum_{i=0}^\infty c_n x^i,\\ &C^2(x) = \sum_{i=0}^\infty (\sum_{j=0}^n c_j c_{i-j})x^i = \sum_{i=0}^\infty c_{i+1}x^i \\ \iff &C(x)=1+xC^2(x) \end{split}$$

  解得

  $$C(x) = \dfrac{1\pm\sqrt{1-4x}}{2x}$$

  显而易见卡特兰数不可能有两个生成函数，考虑取舍。

  我们将 $\sqrt{1-4x}$ 暴力 Maclaurin（麦克劳林） 展开：

  $$\sqrt{1-4x}=1-2x-2x^2 - 4x^3 - 10x^4...$$

  分别代入两个生成函数：

  $$\begin{aligned} &C_1(x)=\dfrac{1+1-2x-2x^2-4x^3-10x^4...}{2x}=x^{-1}-1-x-2x^2-5x^3... \\ &C_2(x)=\dfrac{1-1+2x+2x^2+4x^3+10x^4}{2x} = 1+x+2x+5x^3... \end{aligned}$$

  恭喜你推出了卡特兰数第 -1 项 显然 $C_2$ 才是正确的生成函数。

• 计算公式：

  递归/递推公式：

  $$c_{n} = \begin{cases} 1 &n=0\\ \sum_{0\leq i\leq n-1} c_ic_{n-i-1}&n\geq1 \end{cases}$$
  $$c_n = \dfrac{4n-2}{n+1}c_{n-1}$$

  该式在实际应用中有很多具体意义，见下面的“应用”。

  通项公式：

  $$c_n = \dfrac{\binom{2n}{n}}{n+1}=\binom{2n}{n}-\binom{2n}{n-1}$$

  推导：

  将 $\sqrt{1-4x}$ 泰勒展开（或广义二项式展开）得到$\sqrt{1-4x}=[x^n](-4)^n \binom{\frac{1}{2}}{n}$，进而得到：

$$\begin{aligned} \sqrt{1-4x} &= \sum_0^\infty (-1)^n 2^{2n} \binom{\frac{1}{2}}{n} \\ &= \sum_0^\infty (-1)^n 2^n \frac{(\frac{1}{2})^{\underline{n}}2^n}{n!} \\ &= \sum_0^\infty (-1) 2^n \frac{(2-1)(4-1)...(2n-3)}{n!} \\ &= \sum_0^\infty (-1) 2^n \frac{1}{2n-1}\times\frac{(2n)!2^{-n}}{n!n!} \\ &= \sum_0^\infty \frac{\binom{2n}{n}}{1-2n} \end{aligned}$$

带进生成函数：

$$\begin{aligned} C(x) &= \dfrac{1-\sum_{i=0}^\infty \frac{\binom{2i}{i}}{1-2i}x^i}{2x} \\ &= \sum_{i=0}^\infty \frac{1}{2(2i+1)}{2i+2\choose i+1}x^i \\ &=\sum_{i=0}^\infty\frac{{2i\choose i}}{i+1}x^i \end{aligned}$$

所以可得 $c_n = \dfrac{\binom{2i}{i}}{i+1}$

• 应用：

  • 多边形对角线

    Conclusion: 对于一个凸 n 边形，将其分割为若干三角形的方案数为 $c_{n-2}$.

    Proof: 对于某个点可以与 n-2 个点连线将多边形分成一个 a+1 边形和一个 n-a+1 边形，递归处理。

    根据卡特兰数的定义，即可证明方案数为 $c_{n-2}$。

  • n 次进栈，n 次出栈的合法排列数

    Conclution: 为卡特兰数第 n 项。

    Proof: 通过合法方案减去不合法方案得到答案为 $\binom{2n}{n}-\binom{2n}{n-1}$，发现即为卡特兰数通项公式 $\frac{\binom{2n}{n}}{n+1} = \binom{2n}{n}(1-\frac{n}{n+1})=\binom{2n}{n}-\binom{2n}{n-1}$，故得证。

  • $(0,0)\rightarrow (n,n)$不越过 $y=x$ 的路径数

    Conclusion: 方案数为 $c_n$

    Proof: 略

  • n 对括号完全匹配

    Conclusion: 如题，n 对括号合法匹配数，合法的定义无需解释。

    Proof: 可以令左括号为 1，右括号为 -1，则合法方案数为前缀和不为负的排列方案数。

    那么可以理解为 1 是往右，-1 是往上，则合法方案数为不越过 $y=x$ 的路径数，即上一个应用。

  • n 个节点的二叉树形态数

    Conclusion: 不说了都是卡特兰数。

    Proof: 取出一个作为根的点，就可以递归解决，最后列出和 Catalan 数定义一样的递归式。

  • $\{1,2...2n\}$两两分为 n 个子集，其中元素不交叉的方案数

  • 排队找零问题

    And So On……

• 推广：（ExCatalan）

  可以通过格路径引出这个问题。

  • $(0,0)\rightarrow (n,n)$不越过 $y=x+k$ 的路径数： $\binom{2n}{n}-\binom{2n}{n-k-1}$

  • n 对括号最多失配 k 对的方案数： $\binom{2n}{n}-\binom{2n}{n-k-1}$

    恰好 k 对的方案数： $\binom{2n}{n-k}-\binom{2n}{n-k-1}$

  容易发现，$\binom{2n}{n-m}$ 的含义即为最少完配 n-m 次错误的方案数。

References：#

[1] hxc.(2004).Fake with its applications,『特殊计数数列』,『组合数学总结2：生成函数和特殊计数数列』