树状数组预备
<前言>
本次依旧是高手训练专题解析。
但与以往不同的是,这次会附上树状数组基础内容。
本篇为基础内容。
<树状数组>
在此贴出大哥的blog,有更加全面、系统的介绍。
什么是树状数组?怎么用树状数组?树状数组有什么应用?
什么是树状数组?
树状数组 是一种数据结构, 可以在\(O(log_2 n )\)时间内完成 **修改、查询 **等序列操作。
它可以处理区间、单点加&查询,以及前(后)缀最值。
它利用了\(lowbit()\)运算的一些性质。
观察\(1...10\)的\(\mathrm{lowbit}\)序列:
| 序号 | \(lowbit\) | 二进制 |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 2 | 10 |
| 3 | 1 | 11 |
| 4 | 4 | 100 |
| 5 | 1 | 101 |
| 6 | 2 | 110 |
| 7 | 1 | 111 |
| 8 | 8 | 1000 |
| 9 | 1 | 1001 |
| 10 | 2 | 1010 |
容易发现\(lowbit\)就是在求最低位的1所代表的数。
而我们可以通过补码的性质快速求\(lowbit\)
#define lowbit(x) (x & (-x))
那么我们可以根据这个性质搞出一棵树(森林),使一些点对应一段区间。
大概长这样:(\(\mathrm{x}\)连向\(\mathrm{y}\)的边代表\(\mathrm{y + lowbit(y) = x}\))

那么我们通过改变一个值的大小来代表改变一段区间的(子树)所有数的大小。
比如点\(x\)对应(可以理解为一种代表)\([x - \mathrm{lowbit(x)} + 1, \ x]\)一段区间内的数。对这一段区间进行区间加的时候只需要修改x就行了。
那么对于序列\(\{a_i\}\) ,我们需要维护一个\(\{c_i\}\),定义如下
即\(c_n\)为所有子树内\(a_i\)的和。
如何使用树状数组
我们需要掌握修改、查询等操作
修改
我们进行修改操作的时候,可以选择是进行前缀修改还是后缀修改。
本质上都是利用了树状数组的性质,所以按照习惯来吧。
修改操作之前说过只需要修改某些特定的点就行了。
比如修改\([1,\ 9]\) 一段区间。
我们可以先\([1,\ N]\)修改,再\([9\ +\ 1, N]\)逆修改。
修改之后的树形态: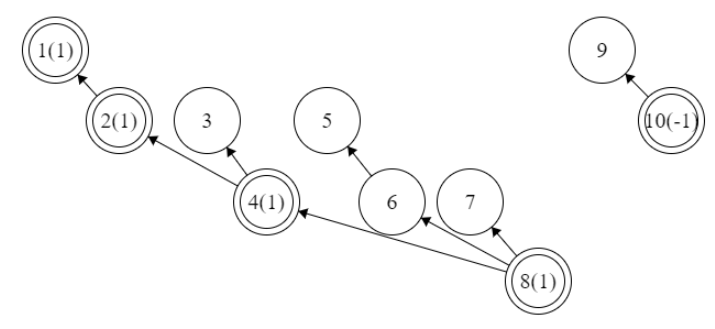
我们只修改了少数点,而且个数是\(\mathrm{O(log_2 n)}\)级别的,数量越大优势越明显。
\(\mathrm{Code:}\)
inline void inc(int x, int v) {for(; x <= MAX
N; x += lowbit(x)) c[x] += v;}
查询
那么有人就要问了,这个修改后的形态这么鬼畜,改怎么获得正确的查询信息呢?
我们发现\(lowbit\)的另一个快乐的性质:
比如上面那个栗子,无论9还是10都可以通过这个运算到达8.
那不是很爽么。单次修改中某个点若在范围内,则其同级子树必有一个被修改。直接通过\(lowbit\)累计即可。
容易发现
我们可以在\(O(log_2n)\)时间内完成查询。
\(\mathrm{Code:}\)
inline int ask(int x) {
int sum = 0;
for (; x; x -= lowbit(x)) sum += c[x];
return sum;
}
一些拓展
比如前缀(后缀)最值,可以通过树状数组快速维护。
代码实现十分简单,只需要将\("+"\) \("-"\)改成\("max"\) \("min"\)
Just like:
inline void inc(int x, int v) {for (; x <= MAXN; x += lowbit(x)) c[x] = max(c[x], v);}
//操作这里min也是一样的
inline int ask(int x) {
int maxn = -1;
for (; x; x -= lowbit(x)) maxn = max(maxn, c[x]); //注释同上
return maxn;
}
二维操作&各种基本功能实现详见Pαrsnip的blog
还有比如什么树状数组上二分(倍增)、一些小Trick、简单代替线段树等黑科技。
尽在cz的树状数组黑科技讲义.
树状数组应用
一维/二维/(你想写高维可能也没什么)的 区间/单点修改,区间/单点查询的 区间四则运算/前缀(后缀)最值。
二维偏序,逆序对等,事实上很多偏序问题树状数组是首选。
当然更多的应用无处不在与各个地方。
题目基本是让你求一个序列中所有连续子序列的某个贡献值。
<后记>
为树状数组专题备用基础讲解的blog。


