libSVM 参数选择

[预测标签，准确率，决策值]=svmpredict(测试标签，测试数据，训练的模型);

原文参考：http://blog.csdn.net/carson2005/article/details/6539192

关于SVM参数c&g选取的总结帖[matlab-libsvm]：http://www.ilovematlab.cn/thread-47819-1-1.html 原文见下方

需要提醒的是，libSVM支持多类分类问题，当有k个待分类问题时，libSVM构建k*（k-1）/2种分类模型来进行分类，即：libSVM采用一对一的方式来构建多类分类器，如下所示：

1 vs 2, 1 vs 3, ..., 1 vs k, 2 vs 3, ..., 2 vs k, ..., k-1 vs k。

-s svm 类型默认是0 c-svc

C_SVC与NU_SVC其实采用的模型相同，但是它们的参数C的范围不同,C_SVC采用的是0到正无穷，NU_SVC是[0,1]。

-g g ：设置核函数中的g ，默认值为1/ k ；其中-g选项中的k是指输入数据中的属性数。

SVM关键是选取核函数的类型，主要有线性内核，多项式内核，径向基内核（RBF），sigmoid核。
这些函数中应用最广的应该就是RBF核了，无论是小样本还是大样本，高维还是低维等情况，RBF核函数均适用，它相比其他的函数有一下优点：
1）RBF核函数可以将一个样本映射到一个更高维的空间，而且线性核函数是RBF的一个特例，也就是说如果考虑使用RBF，那么就没有必要考虑线性核函数了。
2）与多项式核函数相比，RBF需要确定的参数要少，核函数参数的多少直接影响函数的复杂程度。另外，当多项式的阶数比较高时，核矩阵的元素值将趋于无穷大或无穷小，而RBF则在上，会减少数值的计算困难。
3）对于某些参数，RBF和sigmoid具有相似的性能。

为什么要选择RBF

通常而言，RBF核是合理的首选。这个核函数将样本非线性地映射到一个更高维的空间，与线性核不同，它能够处理分类标注和属性的非线性关系。并且，线性核是RBF的一个特例（Keerthi and Lin 2003），因此，使用一个惩罚因子C的线性核与某些参数（C,γ）的RBF核具有相同的性能。同时，Sigmoid核的表现很像一定参数的RBF核（Lin and Link 2003）。
第二个原因，超参数（hyperparameter）的数量会影响到模型选择的复杂度（因为参数只能靠试验呀！）。多项式核比RBF核有更多的超参数。
最后，RBF核有更少的数值复杂度（numerical difficulties）。一个关键点0<Kij<=1对比多项式核，后者关键值需要 infinity(rxiTxj+r>1)或者zero(rxiTxj+r<1)，这是高阶运算。此外，我们必须指出sigmoid核在某些参数下不是合法的（例如，不是两个向量的内积）。（Vapnik 1995）

当然，也存在一些情形RBF核是不适用的。特别地，当特征维数非常大的时候，很可能只能适用线性核。

在某些情况下RBF kernel是不合适的。实际情况中，当特征数非常大时，我们大多会考虑用linear kernel。

nr_weight, weight_label, and weight这三个参数用于改变某些类的惩罚因子。当输入数据不平衡，或者误分类的风险代价不对称的时候，这三个参数将会对样本训练起到非常重要的调节作用。

nr_weight是weight_label和weight的元素个数，或者称之为维数。Weight[i]与weight_label[i]之间是一一对应的，weight[i]代表着类别weight_label[i]的惩罚因子的系数是weight[i]。如果你不想设置惩罚因子，直接把nr_weight设置为0即可。

为了防止错误的参数设置，你还可以调用libSVM提供的接口函数svm_check_parameter()来对输入参数进行检查。

http://blog.csdn.net/heyijia0327/article/details/38090229

径向基(Radial basis function)径向基函数是一类函数，径向基函数是一个它的值(y)只依赖于变量(x)距原点距离的函数，即 $\phi(\mathbf{x}) = \phi(\|\mathbf{x}\|)$ ；也可以是距其他某个中心点的距离，即 $\phi(\mathbf{x}, \mathbf{c}) = \phi(\|\mathbf{x}-\mathbf{c}\|)$ . 引用自wiki . 也就是说，可以选定径向基函数来当核函数，譬如SVM里一般都用高斯径向基作为核函数，但是核函数不一定要选择径向基这一类函数。

接下来将讨论核函数为什么能映射到高维空间，径向基核又为什么能够映射到无限维空间

http://www.cnblogs.com/LeftNotEasy/archive/2011/05/02/basic-of-svm.html整体讲SVM，易懂！

惩罚因子

在式子1中

注意其中C的位置，也可以回想一下C所起的作用（表征你有多么重视离群点，C越大越重视，越不想丢掉它们）。这个式子是以前做SVM的人写的，大家也就这么用，但没有任何规定说必须对所有的松弛变量都使用同一个惩罚因子，我们完全可以给每一个离群点都使用不同的C，这时就意味着你对每个样本的重视程度都不一样，有些样本丢了也就丢了，错了也就错了，这些就给一个比较小的C；而有些样本很重要，决不能分类错误，就给一个很大的C。
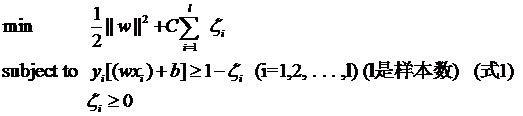
对付数据集偏斜问题的方法之一就是在惩罚因子上作文章，想必大家也猜到了，那就是给样本数量少的负类更大的惩罚因子，表示我们重视这部分样本（本来数量就少，再抛弃一些，那人家负类还活不活了），因此我们的目标函数中因松弛变量而损失的部分就变成了：

其中i=1…p都是正样本，j=p+1…p+q都是负样本。libSVM这个算法包在解决偏斜问题的时候用的就是这种方法。

　　那C₊和C_-怎么确定呢？它们的大小是试出来的（参数调优），但是他们的比例可以有些方法来确定。咱们先假定说C₊是5这么大，那确定C_-的一个很直观的方法就是使用两类样本数的比来算，对应到刚才举的例子，C_-就可以定为500这么大（因为10，000：100=100：1嘛）。

　　但是这样并不够好，回看刚才的图，你会发现正类之所以可以“欺负”负类，其实并不是因为负类样本少，真实的原因是负类的样本分布的不够广（没扩充到负类本应该有的区域）。说一个具体点的例子，现在想给政治类和体育类的文章做分类，政治类文章很多，而体育类只提供了几篇关于篮球的文章，这时分类会明显偏向于政治类，如果要给体育类文章增加样本，但增加的样本仍然全都是关于篮球的（也就是说，没有足球，排球，赛车，游泳等等），那结果会怎样呢？虽然体育类文章在数量上可以达到与政治类一样多，但过于集中了，结果仍会偏向于政治类！所以给C₊和C_-确定比例更好的方法应该是衡量他们分布的程度。比如可以算算他们在空间中占据了多大的体积，例如给负类找一个超球——就是高维空间里的球啦——它可以包含所有负类的样本，再给正类找一个，比比两个球的半径，就可以大致确定分布的情况。显然半径大的分布就比较广，就给小一点的惩罚因子。

但是这样还不够好，因为有的类别样本确实很集中，这不是提供的样本数量多少的问题，这是类别本身的特征（就是某些话题涉及的面很窄，例如计算机类的文章就明显不如文化类的文章那么“天马行空”），这个时候即便超球的半径差异很大，也不应该赋予两个类别不同的惩罚因子。

http://blog.csdn.net/zhzhl202/article/details/7583464

参考文献以及进一步阅读：

1. http://www.blogjava.net/zhenandaci/archive/2009/03/15/259786.html 讲解了SVM引入松弛变量的原因及好处

2. http://www.blogjava.net/zhenandaci/archive/2009/03/06/258288.html SVM中核函数的特性以及在SVM中的作用

3. http://blog.pluskid.org/?tag=support-vector-machine Kid的关于SVM经典文章

http://blog.csdn.net/liulina603/article/details/8552424
svm_type –
指定SVM的类型，下面是可能的取值：
- CvSVM::C_SVC C类支持向量分类机。 n类分组 (n $\geq$ 2)，允许用异常值惩罚因子C进行不完全分类。
- CvSVM::NU_SVC $\nu$ 类支持向量分类机。n类似然不完全分类的分类器。参数为 $\nu$ 取代C（其值在区间【0，1】中，nu越大，决策边界越平滑）。
- CvSVM::ONE_CLASS 单分类器，所有的训练数据提取自同一个类里，然后SVM建立了一个分界线以分割该类在特征空间中所占区域和其它类在特征空间中所占区域。
- CvSVM::EPS_SVR $\epsilon$ 类支持向量回归机。训练集中的特征向量和拟合出来的超平面的距离需要小于p。异常值惩罚因子C被采用。
- CvSVM::NU_SVR $\nu$ 类支持向量回归机。 $\nu$ 代替了 p。
kernel_type –
SVM的内核类型，下面是可能的取值：
- CvSVM::LINEAR 线性内核。没有任何向映射至高维空间，线性区分（或回归）在原始特征空间中被完成，这是最快的选择。 $K(x_i, x_j) = x_i^T x_j$ .
- CvSVM::POLY 多项式内核： $K(x_i, x_j) = (\gamma x_i^T x_j + coef0)^{degree}, \gamma > 0$ .
- CvSVM::RBF 基于径向的函数，对于大多数情况都是一个较好的选择： $K(x_i, x_j) = e^{-\gamma ||x_i - x_j||^2}, \gamma > 0$ .
- CvSVM::SIGMOID Sigmoid函数内核： $K(x_i, x_j) = \tanh(\gamma x_i^T x_j + coef0)$ .
degree – 内核函数（POLY）的参数degree。
gamma – 内核函数（POLY/ RBF/ SIGMOID）的参数 $\gamma$ 。
coef0 – 内核函数（POLY/ SIGMOID）的参数coef0。
Cvalue – SVM类型（C_SVC/ EPS_SVR/ NU_SVR）的参数C。
nu – SVM类型（NU_SVC/ ONE_CLASS/ NU_SVR）的参数 $\nu$ 。
p – SVM类型（EPS_SVR）的参数 $\epsilon$ 。
class_weights – C_SVC中的可选权重，赋给指定的类，乘以C以后变成 $class\_weights_i * C$ 。所以这些权重影响不同类别的错误分类惩罚项。权重越大，某一类别的误分类数据的惩罚项就越大。
term_crit – SVM的迭代训练过程的中止条件，解决部分受约束二次最优问题。您可以指定的公差和/或最大迭代次数。

关于SVM参数c&g选取的总结帖[matlab-libsvm]

写了个程序来选取SVM中参数c和g的最佳值.
[写这个的目的是方便大家用这个小程序直接来寻找c和g的最佳值,不用再另外编写东西了.]
其实原本libsvm C语言版本中有相应的子程序可以找到最佳的c和g,需装载python语言然后用py 那个画图就可以找到最佳的c和g,我写了个matlab版本的.算是弥补了libsvm在matlab版本下的空缺.

测试数据还是我视频里的wine data.

寻找最佳c和g的思想仍然是让c和g在一定的范围里跑(比如 c = 2^(-5),2^(-4),...,2^(5),g = 2^(-5),2^(-4),...,2^(5)),然后用cross validation的想法找到是的准确率最高的c和g,在这里我做了一点修改(纯粹是个人的一点小经验和想法),我改进的是: 因为会有不同的c和g都对应最高的的准确率,我把具有最小c的那组c和g认为是最佳的c和g,因为惩罚参数不能设置太高,很高的惩罚参数能使得validation数据的准确率提高,但过高的惩罚参数c会造成过学习状态,反正从我用SVM到现在,往往都是惩罚参数c过高会导致最终测试集合的准确率并不是很理想..

在使用这个程序时也有小技巧,可以先大范围粗糙的找比较理想的c和g,然后再细范围找更加理想的c和g.

比如首先让 c = 2^(-5),2^(-4),...,2^(5),g = 2^(-5),2^(-4),...,2^(5)在这个范围找比较理想的c和g,如图:
======
<ignore_js_op>

======
此时bestc = 0.5,bestg=1,bestacc = 98.8764[cross validation 的准确率]

最终测试集合的准确率 Accuracy = 96.6292% (86/89) (classification)
======
此时看到可以把c和g的范围缩小.还有步进的大小也可以缩小(程序里都有参数可以自己调节,也有默认值可不调节).
让 c = 2^(-2),2^(-1.5),...,2^(4),g = 2^(-4),2^(-3.5),...,2^(4)在这个范围找比较理想的c和g,如图:
=============
<ignore_js_op>

===============
此时bestc = 0.3536,bestg=0.7017,bestacc = 98.8764[cross validation 的准确率]
最终测试集合的准确率 Accuracy = 96.6292% (86/89) (classification)
===================
上面第二个的测试的代码:

load wine_SVM;
train_wine = [wine(1:30,:);wine(60:95,:);wine(131:153,:)];
train_wine_labels = [wine_labels(1:30);wine_labels(60:95);wine_labels(131:153)];
test_wine = [wine(31:59,:);wine(96:130,:);wine(154:178,:)];
test_wine_labels = [wine_labels(31:59);wine_labels(96:130);wine_labels(154:178)];
[train_wine,pstrain] = mapminmax(train_wine');
pstrain.ymin = 0;
pstrain.ymax = 1;
[train_wine,pstrain] = mapminmax(train_wine,pstrain);
[test_wine,pstest] = mapminmax(test_wine');
pstest.ymin = 0;
pstest.ymax = 1;
[test_wine,pstest] = mapminmax(test_wine,pstest);
train_wine = train_wine';
test_wine = test_wine';
[bestacc,bestc,bestg] = SVMcg(train_wine_labels,train_wine,-2,4,-4,4,3,0.5,0.5,0.9);
cmd = ['-c ',num2str(bestc),' -g ',num2str(bestg)];
model = svmtrain(train_wine_labels,train_wine,cmd);
[pre,acc] = svmpredict(test_wine_labels,test_wine,model);

复制代码

============我写的那个选取SVM中参数c和g的最佳值.的程序的代码 SVMcg.m====================

function [bestacc,bestc,bestg] = SVMcg(train_label,train,cmin,cmax,gmin,gmax,v,cstep,gstep,accstep)
%SVMcg cross validation by faruto
%Email:farutoliyang@gmail.com QQ:516667408 http://blog.sina.com.cn/faruto BNU
%last modified 2009.8.23
%Super Moderator @ www.ilovematlab.cn
%% about the parameters of SVMcg
if nargin < 10
accstep = 1.5;
end
if nargin < 8
accstep = 1.5;
cstep = 1;
gstep = 1;
end
if nargin < 7
accstep = 1.5;
v = 3;
cstep = 1;
gstep = 1;
end
if nargin < 6
accstep = 1.5;
v = 3;
cstep = 1;
gstep = 1;
gmax = 5;
end
if nargin < 5
accstep = 1.5;
v = 3;
cstep = 1;
gstep = 1;
gmax = 5;
gmin = -5;
end
if nargin < 4
accstep = 1.5;
v = 3;
cstep = 1;
gstep = 1;
gmax = 5;
gmin = -5;
cmax = 5;
end
if nargin < 3
accstep = 1.5;
v = 3;
cstep = 1;
gstep = 1;
gmax = 5;
gmin = -5;
cmax = 5;
cmin = -5;
end
%% X:c Y:g cg:acc
[X,Y] = meshgrid(cmin:cstep:cmax,gmin:gstep:gmax);
[m,n] = size(X);
cg = zeros(m,n);
%% record acc with different c & g,and find the bestacc with the smallest c
bestc = 0;
bestg = 0;
bestacc = 0;
basenum = 2;
for i = 1:m
for j = 1:n
cmd = ['-v ',num2str(v),' -c ',num2str( basenum^X(i,j) ),' -g ',num2str( basenum^Y(i,j) )];
cg(i,j) = svmtrain(train_label, train, cmd);
if cg(i,j) > bestacc
bestacc = cg(i,j);
bestc = basenum^X(i,j);
bestg = basenum^Y(i,j);
end
if ( cg(i,j) == bestacc && bestc > basenum^X(i,j) )
bestacc = cg(i,j);
bestc = basenum^X(i,j);
bestg = basenum^Y(i,j);
end
end
end
%% to draw the acc with different c & g
[C,h] = contour(X,Y,cg,60:accstep:100);
clabel(C,h,'FontSize',10,'Color','r');
xlabel('log2c','FontSize',10);
ylabel('log2g','FontSize',10);
grid on;

复制代码

=====================================

这样那个libsvm-matlab工具箱我就有了自己的一个升级版本的了.大家可以把这个SVMcg.m加进去一起用了...
<ignore_js_op>

libsvm-mat-2.89-3[faruto version].rar (76.46 KB, 下载次数: 1853)
里面有SVMcg.m使用说明.如下:
[bestacc,bestc,bestg] = SVMcg(train_label,train,cmin,cmax,gmin,gmax,v,cstep,gstep,accstep)

train_label:训练集标签.要求与libsvm工具箱中要求一致.
train:训练集.要求与libsvm工具箱中要求一致.
cmin:惩罚参数c的变化范围的最小值(取以2为底的对数后),即 c_min = 2^(cmin).默认为 -5
cmax:惩罚参数c的变化范围的最大值(取以2为底的对数后),即 c_max = 2^(cmax).默认为 5
gmin:参数g的变化范围的最小值(取以2为底的对数后),即 g_min = 2^(gmin).默认为 -5
gmax:参数g的变化范围的最小值(取以2为底的对数后),即 g_min = 2^(gmax).默认为 5

v:cross validation的参数,即给测试集分为几部分进行cross validation.默认为 3
cstep:参数c步进的大小.默认为 1
gstep:参数g步进的大小.默认为 1
accstep:最后显示准确率图时的步进大小. 默认为 1.5
[上面这些参数大家可以更改以期达到最佳效果,也可不改用默认值]
<ignore_js_op>

posted @ 2015-06-19 20:24 菜鸡一枚阅读(2550) 评论(0) 编辑收藏举报

刷新页面返回顶部

菜鸡一枚

libSVM 参数选择

libSVM 参数选择

http://blog.csdn.net/heyijia0327/article/details/38090229

惩罚因子

公告