如何分析算法的「时间复杂度」?
如何分析算法的「时间复杂度」?
做为程序员我们都知道数据结构和算法十分重要,同时学好数据结构和算法对大多数程序员来说也是相当困难的一件事情,不得不承认自己也是这大部分中的其中一个 ,但是如果想让自己的编程之路走的更长远,必须要啃下这块难啃的骨头 。所以我准备认真的开始了,希望自己可以坚持下去。喜欢的希望帮忙点个赞 啊
复杂度分析是整个算法学习的精髓,只要掌握了它,数据结构和算法的内容基本上就掌握了一半。所以这篇文章主要是讲如何进行算法的复杂度分析,主要是参考极客时间王争老师的数据结构与算法课程,自己进行了总结抽象,有兴趣的可以去购买课程学习啊。
对数据结构和算法的一些认识
数据结构就是指一组数据的存储结构。算法就是操作数据的一组方法。
数据结构和算法是相辅相成的。数据结构是为算法服务的,算法要作用在特定的数据结构之上。因此我们无法孤立数据结构来讲算法,也无法孤立算法来讲数据结构。比如,因为数组具有随机访问的特点,常用的二分查找算法需要用数组来存储数据。但如果我们选择链表这种数据结构,二分查找算法就无法工作了,因为链表并不支持随机访问。
数据结构是静态的,它只是组织数据的一种方式。如果不在它的基础上操作、构建算法,孤立存在的数据结构就是没用的。
为什么要进行复杂度分析
数据结构和算法本身解决的是“快”和“省”的问题,即如何让代码运行得更快,如何让代码更省存储空间。所以,执行效率是算法一个非常重要的考量指标。
我们可以通过事后统计法(把代码跑一遍,通过统计、监控,就能得到算法执行的时间和占用的内存大小)来评估算法执行效率的,但是这种方法有非常大的局限性。
- 测试结果非常依赖测试环境。
- 测试结果受数据规模的影响很大。 比如,对于小规模的数据排序,插入排序可能反倒会比快速排序要快
所以,我们需要一个不用具体的测试数据来测试,就可以粗略地估计算法的执行效率的方法,这就是渐进时间,空间复杂度分析也就是我们所说的复杂度分析。
渐进时间,空间复杂度分析为我们提供了一个很好的理论分析的方向,并且它是宿主平台无关的,能够让我们对我们的程序或算法有一个大致的认识,让我们知道,比如在最坏的情况下程序的执行效率如何,同时也为我们交流提供了一个不错的桥梁,我们可以说,算法1的时间复杂度是O(n),算法2的时间复杂度是O(logN),这样我们立刻就对不同的算法有了一个“效率”上的感性认识。
当然,渐进式时间,空间复杂度分析只是一个理论模型,只能提供粗略的估计分析,我们不能直接断定就觉得O(logN)的算法一定优于O(n), 针对不同的宿主环境,不同的数据集,不同的数据量的大小,在实际应用上面可能真正的性能会不同,所以,针对不同的实际情况,可以进行一定的性能基准测试,比如在统一一批手机上(同样的硬件,系统等等)进行横向基准测试,进而选择适合特定应用场景下的最有算法。
所以,渐进式时间,空间复杂度分析与事后统计法并不冲突,而是相辅相成的,但是一个低阶的时间复杂度程序有极大的可能性会优于一个高阶的时间复杂度程序,所以在实际编程中,时刻关心理论时间,空间度模型是有助于产出效率高的程序的。同时,因为渐进式时间,空间复杂度分析只是提供一个粗略的分析模型,因此也不会浪费太多时间,重点在于在编程时,要具有这种复杂度分析的思维,这有助于我们不断提示自己编程水平,提高代码质量。
大O复杂度表示法
算法的执行效率,粗略地讲,就是算法代码执行的时间。 那我我们怎样直接可以看出一段代码的执行效率呢?接下来举几个实际的例子
示例1:
假设每段代码的执行时间都是一样的,为unit_time。那么如下这段代码的时间复杂度是多少?
function sum(n){
let sum = 0;
let i = 1;
for(i; i <= n; i++){
sum += i;
}
return sum;
}分析过程如下图所示

T(n)=(3n+2)*unit_time。可以看出来,所有代码的执行时间 T(n) 与每行代码的执行次数成正比。
示例2:
我们继续运用上面的方法分析下下面这段代码
function sum(n){
let sum = 0;
let i = 1;
for(i; i <= n; i++){
console.log('test');
for(let j = 1; j <= n; j++){
sum = sum + i * j;
}
}
return sum;
}分析过程如下图所示

综上:虽然我们不知道 unit_time 的具体值,但是通过这两段代码执行时间的推导过程,我们可以得到一个非常重要的规律,所有代码的执行时间 T(n) 与每行代码的执行次数 n 成正比。
我们可以把这个规律总结成一个公式: T(n) = O(f(n)),这时候我们的大 O 就出现了

所以,第一个例子中的 T(n) = O(3n+2),第二个例子中的 T(n) = O(2n2+2n+3)。就是大 O 时间复杂度表示法。大 O 时间复杂度实际上并不具体表示代码真正的执行时间,而是表示代码执行时间随数据规模增长的变化趋势,所以,也叫作渐进时间复杂度(asymptotic time complexity),简称时间复杂度。
当 n 很大时,你可以把它想象成 10000、100000。公式中的低阶、常量、系数三部分并不左右增长趋势,所以都可以忽略。我们只需要记录一个最大量级就可以了,如果用大 O 表示法表示刚讲的那两段代码的时间复杂度,就可以记为:T(n) = O(n); T(n) = O(n2)。
时间复杂度分析三个实用方法
只关注循环执行次数最多的一段代码
大O这种复杂度表示方法只是关注代码执行时间随数据规模增长的变化趋势。通常会忽略掉低阶、常量、系数,只需要记录一个最大的量级就可以。
所以,我们在分析一个算法、一段代码的时间复杂度的时候,也只关注循环执行次数最多的那一段代码就可以了。
还是上面的sum求和代码为例,这段代码的时间复杂度就是O(n)

加法法则:总复杂度等于量级最大的那段代码的复杂度
我们可以看下下面这段代码
function sum(n){
let sum_1 = 0;
for(let i = 1; i < 100; i++){
sum_1 += i;
}
let sum_2 = 0;
for(let j = 0; j < n; j++){
sum_2 += j;
}
let sum_3 = 0;
for(let i = 1; i <= n; i++){
console.log(i);
for(let j = 1; j <= n; j++){
sum_3 = sum_3 + i * j;
}
}
return sum_1 + sum_2 + sum_3;
}我们对代码进行复杂度分析

特别说明下第一段代码:这段代码循环 10000 次、100000 次,只要是一个已知的数,跟 n 无关,照样也是常量级的执行时间。虽然当这个常量很大时对代码执行时间会有很大影响,但是回到时间复杂度的概念来说,它表示的是一个算法执行效率与数据规模增长的变化趋势,所以不管常量的执行时间多大,我们都可以忽略掉。因为它本身对增长趋势并没有影响。
总结下:总的时间复杂度就等于量级最大的那段代码的时间复杂度。可以抽象成如下公式
如果 T1(n)=O(f(n)),T2(n)=O(g(n));那么 T(n)=T1(n)+T2(n)=max(O(f(n)), O(g(n))) =O(max(f(n), g(n)))
乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
理解了加法法则,那么乘法法则应该也很容易理解了,乘法法则公式可以抽象为如下公式
*如果 T1(n)=O(f(n)),T2(n)=O(g(n));那么 T(n)=T1(n)T2(n)=O(f(n))xO(g(n)),O(g(n)))=O(f(n)xg(n))
也就是说,假设 T1(n) = O(n),T2(n) = O(n2),则 T1(n) * T2(n) = O(n3)。 来看下下面这段示例代码
function sum(n){
let sum = 0;
for(let i = 1; i < 100; i++){
sum = sum + fSum(i);
}
}
function fSum(n){
let total = 0;
for(let i = 0; i < n; i++){
total += i;
}
return total
}具体分析如下:
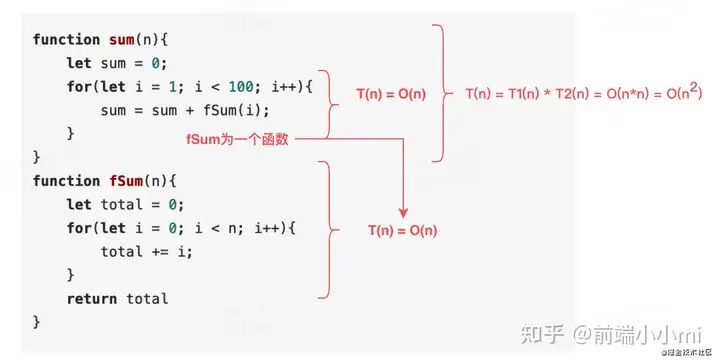
也就是说我们可以把乘法法则看成是嵌套循环
几种常见时间复杂度实例分析

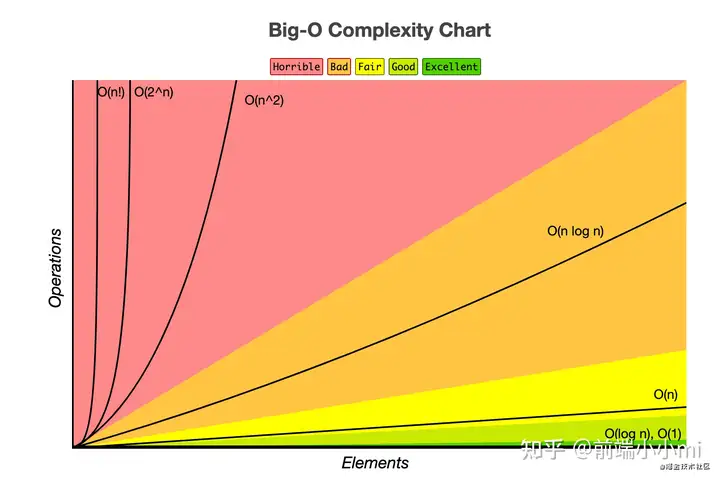
对于上面的几种量级的复杂度可以足略的分为两类
- 多项式量级,如图中的第一列
- 非多项式级,非多项式量级只有两个:O(2n) 和 O(n!),当数据规模 n 越来越大时,非多项式量级算法的执行时间会急剧增加,求解问题的执行时间会无限增长,所以,非多项式时间复杂度的算法其实是非常低效的算法。如下是对常用的多项式量级复杂度的讲解
O(1)
O(1) 只是常量级时间复杂度的一种表示方法,并不是指只执行了一行代码。如下面这段代码,虽然只有 3 行,它的时间复杂度也是 O(1),而不是 O(3)。
let i = 8;
let j = 6;
let sum = i + j;我稍微总结一下,只要代码的执行时间不随 n 的增大而增长,这样代码的时间复杂度我们都记作 O(1)。或者说,一般情况下,只要算法中不存在循环语句、递归语句,即使有成千上万行的代码,其时间复杂度也是Ο(1)。
O(logn)、O(nlogn)
对数阶时间复杂度是常见且比较难分析的一种时间复杂度。可以通过下面这个例子说明
let i=1;
while (i <= n) {
i = i * 2;
}根据前面讲的复杂度分析方法,第三行代码是循环执行次数最多的。所以,只要能计算出这行代码被执行了多少次,就能知道整段代码的时间复杂度。
从代码中可以看出,变量 i 的值从 1 开始取,每循环一次就乘以 2。当大于 n 时,循环结束。还记得我们高中学过的等比数列吗?实际上,变量 i 的取值就是一个等比数列。如果我把它一个一个列出来,就应该是这个样子的:

所以,我们只要知道 x 值是多少,就知道这行代码执行的次数了。通过 2x=n 求解 x 这个问题我们想高中应该就学过了,我就不多说了。x=log2n,所以,这段代码的时间复杂度就是 O(log2n)。
同理下面这段代码的时间复杂度是多少呢?
let i=1;
while (i <= n) {
i = i * 3;
}根据上面所讲的我们可以得出其时间复杂度为O(log3n)。
但是实际上,不管是以 2 为底、以 3 为底,还是以 10 为底,我们可以把所有对数阶的时间复杂度都记为 O(logn),为什么呢?
解答这个问题我们需要了解对数的知识。对数之间是可以相互转化的
log3n=log32∗log2n
因为log32是常量,基于我们前面的一个理论:在采用大 O 标记复杂度的时候,可以忽略系数,即 O(Cf(n)) = O(f(n))。所以,O(log2n) 就等于 O(log3n)
如果理解了前面讲的 O(logn),那 O(nlogn) 就很容易理解了。乘法法则中讲过如果一段代码的时间复杂度是 O(logn),我们循环执行 n 遍,时间复杂度就是 O(nlogn) 了。而且,O(nlogn) 也是一种非常常见的算法时间复杂度。比如,归并排序、快速排序的时间复杂度都是 O(nlogn)。
O(m+n)、O(m*n)
先看下下面这段代码
function cal(m, n) {
let sum_1 = 0;
let i = 1;
for (; i < m; ++i) {
sum_1 = sum_1 + i;
}
let sum_2 = 0;
let j = 1;
for (; j < n; ++j) {
sum_2 = sum_2 + j;
}
return sum_1 + sum_2;
}这段代码的复杂度由两个数据的规模来决定。m 和 n 是表示两个数据规模。我们无法事先评估 m 和 n 谁的量级大,所以我们在表示复杂度的时候,就不能简单地利用加法法则,省略掉其中一个。所以,上面代码的时间复杂度就是 O(m+n)
针对这种情况,原来的加法法则就不正确了,我们需要将加法规则改为:T1(m)+T2(n)=O(f(m)+g(n))。但是乘法法则继续有效:T1(m)∗T2(n)=O(f(m)∗f(n))。
空间复杂度分析
时间复杂度的全称是渐进时间复杂度,表示算法的执行时间与数据规模之间的增长关系。类比一下,空间复杂度全称就是渐进空间复杂度(asymptotic space complexity),表示算法的存储空间与数据规模之间的增长关系。
还是举个C的例子说明
void print(int n) {
int i = 0;
int[] a = new int[n];
for (i; i <n; ++i) {
a[i] = i * i;
}
for (i = n-1; i >= 0; --i) {
print out a[i]
}
}说明如下图

所以整段代码的空间复杂度就是 O(n)
我们常见的空间复杂度就是 O(1)、O(n)、O(n2 ),像 O(logn)、O(nlogn) 这样的对数阶复杂度平时都用不到。而且,空间复杂度分析比时间复杂度分析要简单很多
不同数据结构和算法的复杂度
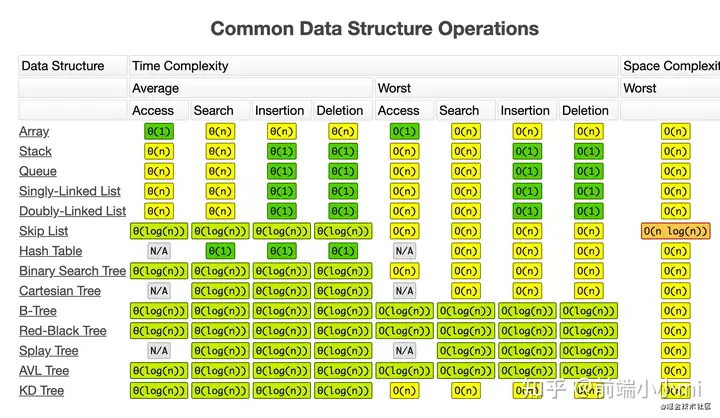
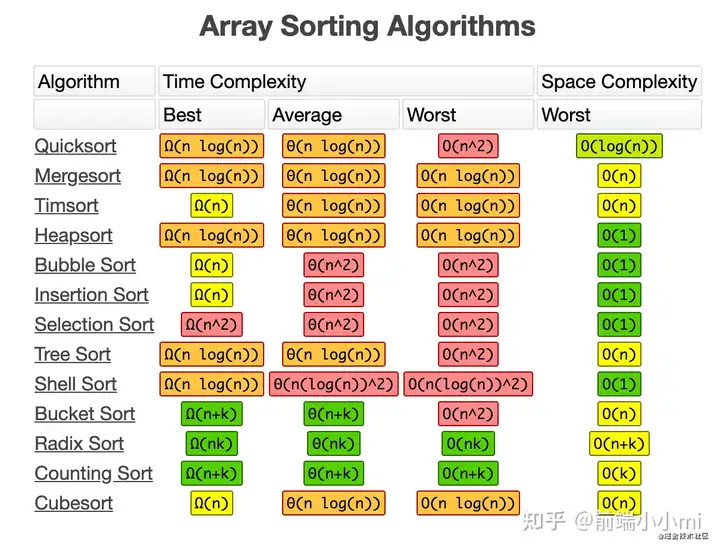
喜欢的可以帮忙点赞收藏哈,谢谢~




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律
2015-09-06 问题:在什么场合应当用几何平均值,而不是用算术平均值?!