triplet loss原理推导及其代码实现
triplet loss原理推导及其代码实现
关于triplet loss原理及推导,参考来源:
【前言】
最近,learning to rank 的思想逐渐被应用到很多领域,比如google用来做人脸识别(faceNet),微软Jingdong Wang 用来做 person-reid 等等。learning to rank中其中重要的一个步骤就是找到一个好的similarity function,而triplet loss是用的非常广泛的一种。
【理解triplet】
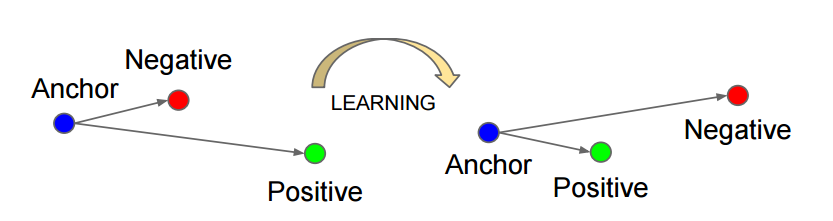
如上图所示,triplet是一个三元组,这个三元组是这样构成的:从训练数据集中随机选一个样本,该样本称为Anchor,然后再随机选取一个和Anchor (记为x_a)属于同一类的样本和不同类的样本,这两个样本对应的称为Positive (记为x_p)和Negative (记为x_n),由此构成一个(Anchor,Positive,Negative)三元组。
【理解triplet loss】
有了上面的triplet的概念, triplet loss就好理解了。针对三元组中的每个元素(样本),训练一个参数共享或者不共享的网络,得到三个元素的特征表达,分别记为: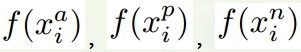
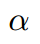
对应的目标函数也就很清楚了:
这里距离用欧式距离度量,+表示[]内的值大于零的时候,取该值为损失,小于零的时候,损失为零。
由目标函数可以看出:
- 当x_a与x_n之间的距离 < x_a与x_p之间的距离加
时,[]内的值大于零,就会产生损失。
- 当x_a与x_n之间的距离 >= x_a与x_p之间的距离加
时,损失为零。
【triplet loss 梯度推导】
上述目标函数记为L。则当第i个triplet损失大于零的时候,仅就上述公式而言,有:
【算法实现时候的提示】
可以看到,对x_p和x_n特征表达的梯度刚好利用了求损失时候的中间结果,给的启示就是,如果在CNN中实现 triplet loss layer, 如果能够在前向传播中存储着两个中间结果,反向传播的时候就能避免重复计算。这仅仅是算法实现时候的一个Trick。
下面是关于triplet loss的matlab代码实现,参考来源:
**摘要:**triplet loss 可以提高特征匹配的性能,可用物体识别,人脸识别,检索等方面,本文用matlab实现triplet loss。
triplet loss 就是学习一个函数隐射, 从特征 映射到 , 有如下关系:. 在一个特征空间中,我们通过欧式距离度量两个特征向量的距离。 triplet loss 的目的在于使同一个类别在空间中靠近,不同类别在空间中远离,那么我们就可以抽象为如下优化函数:
其中, 是锚点,是正样本点,它和属于同一类别,是负样本点,它和不属于同一类别。
这样我们可以通过无约束优化来约束上面函数。
function demo_tripletloss
clear all
clc
data{1} = rand(600,300);
data{2} = rand(600,300);
data{3} = rand(600,300);
inputSize = 600;
hiddenSize = 400;
theta = initializeParameters(hiddenSize, inputSize);
addpath minFunc/
options.Method = 'cg'; % Here, we use L-BFGS to optimize our cost
% function. Generally, for minFunc to work, you
% need a function pointer with two outputs: the
% function value and the gradient. In our problem,
% sparseAutoencoderCost.m satisfies this.
options.maxIter = 400; % Maximum number of iterations of L-BFGS to run
options.display = 'on';
[opttheta, cost] = minFunc( @(p) tripletCost(p, inputSize, hiddenSize, data),theta, options);tripletCost.m
function [cost,grad] = tripletCost(theta, inputSize, hiddenSize, data)
%================================================
%何凌霄 中科院自动化所
%创建时间:2016年5月25日
%================================================
% data: trainning sample for triplet loss
% W: transformer matrix
% cost: cost function
% grad: gradient direction
W = reshape(theta, hiddenSize, inputSize);
% Cost and gradient variables (your code needs to compute these values).
% Here, We initialize them to zeros.
cost = 0;
Wgrad = zeros(size(W));
% the gradient descent update to W1 Would be W1 := W1 - alpha * W1grad, and similarly for W2, b1, b2.
%
[n m] = size(data{1});%m: the number of samples,m:the dim of feature
bias = 0.2;
%forWard
% calc cost
for i = 1:m
cost = cost + ((W*data{1}(:,i) - W*data{2}(:,i))'*(W *data{1}(:,i) - W*data{2}(:,i)) - (W*data{1}(:,i) - W*data{3}(:,i))'*(W *data{1}(:,i) - W*data{3}(:,i)) +bias)/m;
end
%calc gradient
%计算W1grad
Wgrad = (2*W*((data{1} - data{2})*(data{1} - data{2})' - (data{1} - data{3})*(data{1} - data{3})'))/m;
%-------------------------------------------------------------------
% After computing the cost and gradient, We Will convert the gradients back
% to a vector format (suitable for minFunc). Specifically, We Will unroll
% your gradient matrices into a vector.
grad = Wgrad(:);
end
initializeParameters.m
function theta = initializeParameters(hiddenSize, inputSize)
% Initialize parameters randomly based on layer sizes.
r = sqrt(6) / sqrt(hiddenSize+inputSize+1); % we'll choose weights uniformly from the interval [-r, r]
W1 = rand(hiddenSize, inputSize) * 2 * r - r;
theta = W1(:);
end
另外需要一个优化包见资源.
下面是本人关于triplet loss原理推导的一些补充。在上文关于triplet loss的原理推导过程中,有一点容易被忽视,这一点在真正去实现其代码的时候就会发现,无从下手,因为我们要求关于参数的偏导。那么在triplet loss中谁是真正的参数呢(尤其在深度学习中)?很明显在上文的推导过程中我们没看到参数。真正的参数是f这个映射,即把xi映射为一种表示,通常为(w0,w1,...,wn).*(1,x1,...,xn),这里的参数w就是要学习的参数,需要通过triplet loss的梯度反向传播。

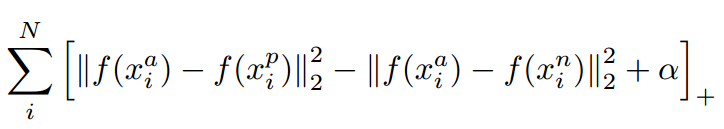
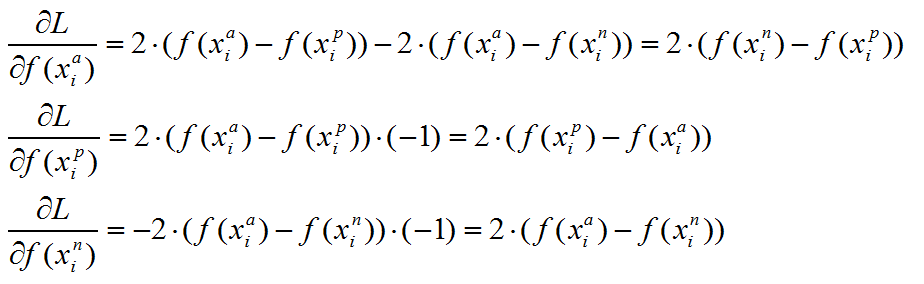

 浙公网安备 33010602011771号
浙公网安备 33010602011771号