NIPS 2015 Part 1

NIPS 2015 Part 1

NIPS has grown to 3755 participants this year with 21.9% acceptance rate, 11% deep learning, 42 sponsors, 101 area chairs, 1524 reviewers. Here are some posters from the first night that I thought were excellent (Part 2). They arranged the posters using KPCA axis that approximately aligned with deep-to-non-deep, so the first 40 posters or so were heavy on deep-learning.

Deep temporal sigmoid belief networks for sequence modeling
Zhe Gan, Chunyuan Li, Ricardo Henao, David E. Carlson, Lawrence Carin

They propose a pair of probabilistic time series models for variational inference (one generative and one recognition model) and use variance controlled log-derivative trick to do stochastic optimization. Using a binary vector, they can model an exponentially large state space, and further introduce hierarchy (deep structure) that can produce longer time scale nonlinear dependences. Each node is extremely simple: linear-logistic-Bernoulli. Zhe told he that they applied to 3-bouncing-balls video dataset represented as 900 dimensional vector, but the generated samples were not perfect and balls would often get stuck. [code on github]

Variational dropout and the local reparameterization trick [arXiv]
Diederik P. Kingma, Tim Salimans, Max Welling

They apply the SGVB reparameterization trick to parameters instead of latent variables. Most importantly, they chose a reparametrization such that the noise is independent for each observation. Upper figure (from dpkingma.com) illustrates the parameterization with slow learning due to the noise being correlated with all samples in the mini-batch, while the lower figure shows the independent form. This relates to variational interpretation of dropout, but now the dropout rate can be learned in a more principled manner.

 

Local expectation gradients for black box variational inference
Michalis Titsias, Miguel Lázaro-Gredilla

The two mains tricks for estimating stochastic gradient for  are the log-derivative trick, and the reparameterization trick (used by the first two papers I introduced above). Reparameterization has much smaller variance, hence leads to faster convergence, however, it can only be used for continuous x and differentiable f. Here authors propose an extension of the log-derivative trick with small variance by (numerically) integrating over 1d over the latent variable that is directly controlled by the corresponding parameter, while holding the Markov blanket constant.

A recurrent latent variable model for sequential data
Junyoung Chung, Kyle Kastner, Laurent Dinh, Kratarth goel, Aaron C. Courville, Yoshua Bengio

In conventional recurrent neural network (RNN), noise is limited to the input/output space, and the internal states are deterministic. Authors add a stochastic latent variable node to an RNN, and incorporate variational autoencoder (VAE) concepts. Latents are only time dependent through the deterministic recurrent states (with hidden LSTM units), and had a much lower dimension. They train on raw waveform of speech, and were able to generate mumbling sound that resembles the speech (I sampled their cool audio), and similarly for 2D handwriting. Their model seemed to work equally well with different complexity of observation models, unlike plain RNNs which require complex observation models to generate reasonable output. [code on github]

Texture synthesis using convolutional neural networks
Leon Gatys, Alexander S. Ecker, Matthias Bethge

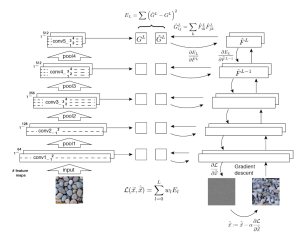To generate texture images, they started with a deep convolutional neural network, and trained another network’s input with fixed weights until the covariance in certain layers matched. If they started with a white noise image, they could sample textures (via gradient descent optimization). [code on github]