NOIP--线段树套线段树
作用
可以解决矩阵区域修改问题。
实现
先按照行建立线段树,然后在行线段树的每个节点下再按照列建立线段树。以2*3的矩阵为例,如下:
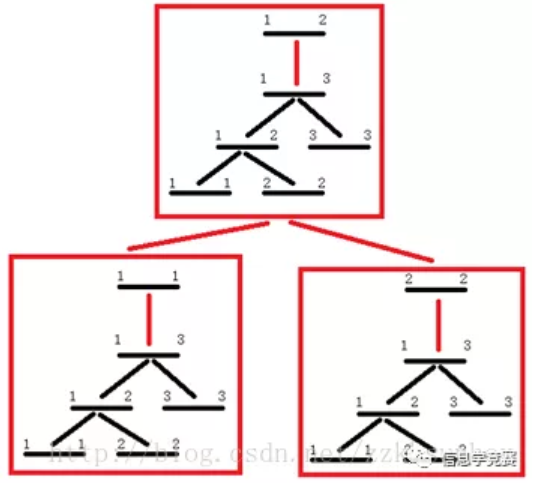
我们称外层的为x树,内层的为y树。
1.单点修改
对于y树的修改,就和普通线段树一样,主要就是x树的修改稍有不同。
①当前x树节点是叶节点
修改这个x树节点所对应的y树,由于是单点修改,找到y树叶节点时,直接修改。
②当前x树节点不是叶节点
修改这个x树节点所对应的y树,同理找到y树叶节点,但是不能直接修改,而是要从当前x树的儿子所对应的y树的相同的叶节点更新上来(因为不仅y树是单点修改,x树也是),可能有点绕,画个图:
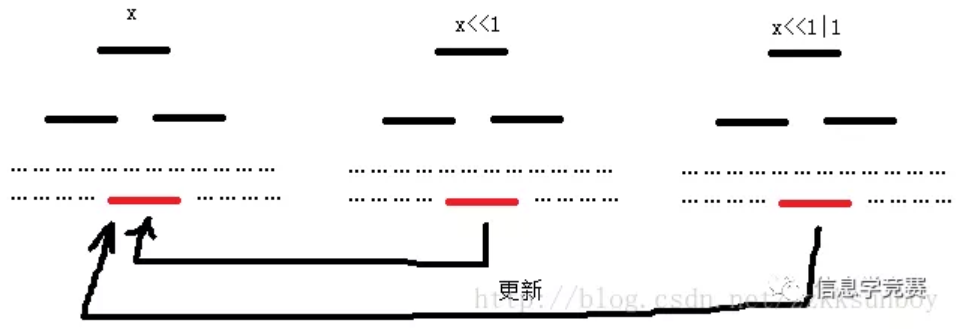
因为每棵y树结构一样,所以就可以较方便实现更新(一般用完全二叉树法存线段树套线段树,不用链式存,因为链式找不同x树的相同y树节点有点麻烦,但不是不可以,留给读者自己思考啦)。
2.查询
查询就很简单了,由于修改时节点信息都修正过了,所以和普通线段树一模一样。
ps:多行修改很难实现,因为x树的Lazy-tag是区间,无法合并。
例题:
题意:一个矩阵初始值都为0,每次给“C X1 Y1 X2 Y2" 去反转这个矩阵。或者"Q X1 Y1"查询这个点是0/1。
第一次接触树套树的题目。
一句AC:对于基本的线段树,再在每个节点建一个y方向上的线段树。tree[n][m]
这道题目更新的时候,对于X方向就是(X1,X2)这个区间,再在其上对Y1,Y2进行更新。
对于查询,X方向上,自顶向下到X1都要对Y进行查询(更新的区间必包括该点),Y方向上则更新到Y1.
-
#include <stdio.h>
-
#include <string.h>
-
#define MAXN 1005
-
#define mem(a) memset(a, 0, sizeof(a))
-
-
bool tree[MAXN<<2][MAXN<<2];
-
int X, N, T;
-
int num, X1, X2, Y1, Y2;
-
char ch[10];
-
-
-
void updatey(int yl,int yr,int xp,int yp)
-
{
-
if(Y1<=yl && yr<=Y2)
-
{
-
tree[xp][yp]=!tree[xp][yp];
-
return;
-
}
-
int mid=(yl+yr)>>1;
-
if(Y1<=mid) updatey(yl,mid,xp,yp<<1);
-
if(Y2>mid ) updatey(mid+1,yr,xp,yp<<1|1);
-
}
-
-
void updatex(int xl,int xr,int xp)
-
{
-
if(X1<=xl && xr<=X2)
-
{
-
updatey(1,N,xp,1);
-
return;
-
}
-
int mid=(xl+xr)>>1;//下面这句刚开始写错了,按照build写了,忘记是个更新操作...
-
if(X1<=mid) updatex(xl,mid,xp<<1);
-
if(X2>mid) updatex(mid+1,xr,xp<<1|1);
-
}
-
void queryy(int yl,int yr,int xp,int yp)
-
{
-
num+=tree[xp][yp];
-
if(yl==yr)
-
return;
-
int mid=(yl+yr)>>1;
-
if(Y1<=mid) queryy(yl,mid,xp,yp<<1);
-
else queryy(mid+1,yr,xp,yp<<1|1);
-
-
}
-
void queryx(int xl,int xr,int xp)
-
{
-
queryy(1,N,xp,1);
-
if(xl==xr)
-
return;
-
int mid=(xl+xr)>>1;
-
if(X1<=mid) queryx(xl,mid,xp<<1);
-
else queryx(mid+1,xr,xp<<1|1);
-
}
-
int main()
-
{
-
while(~scanf("%d", &X))while(X--)
-
{
-
mem(tree);
-
scanf("%d %d%*c", &N,&T);
-
for(int i=0;i<T;i++)
-
{
-
scanf("%s%d%d",ch,&X1,&Y1);
-
if(ch[0]=='Q') num=0,queryx(1,N,1),printf("%d\n",num%2);
-
else
-
{
-
scanf("%d%d",&X2,&Y2);
-
updatex(1,N,1);
-
}
-
}
-
if(X) printf("\n");
-
}
-
return 0;
-
}
NOIP信息学视频地址
视频地址
链接:https://pan.baidu.com/s/1tHo1DFMaDuMZAemNH60dmw
提取码:7jgr


