NOIP--OI省选算法之莫队算法+分块实现
莫队算法是离线处理查询操作的利器。它巧妙地利用了分块的思想。
当有多个查询操作,而且没有修改操作时,我们可以对查询进行离线处理。而通过适当的顺序安排可以加快算法的效率。
一、序列上的分块
如果知道了询问[L, R]区间中的答案,左右端点位置L,R可以通过适当的偏移,而得到区间[L’, R’]的答案,且偏移的复杂度不高(比如说,查询范围扩大或缩小1个单位是O(1)的),那么可以考虑使用一种分块的方法,使询问的区间变得有序。
(如果不对询问的顺序进行处理,简单的偏移不能优化算法的理论复杂度)
把序列分成[√N ]块,每块的长度为N/[√N ]。
对于询问,按左端点所处的块的编号作为第一关键字,右端点作为第二关键字排序。
这样排序,我们来左右端点总共偏移的次数。
当左端点处于同一块时,它只会在块内左右移动,偏移量最多为[√N ];而左端点所处块变化时,偏移次数也最多是2[√N ]。所以,左端点的总偏移次数为M [√N ](M为操作数)。形象的图如下:
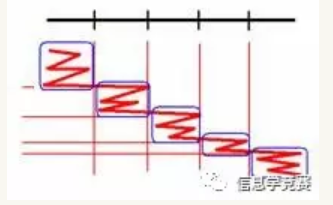
(红色粗线表示左端点限制在每一块内的移动)
右端点呢?对于左端点处于同一块的,右端点从小到大移动,所以对于左端点处在的这一块,右端点最多偏移的次数为N。而一共有[√N ]块,所以右端点的移动次数为N[√N ]。形象的图如下:
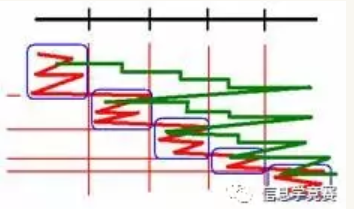
(绿色粗线表示右端点的移动,对于同一块,右端点最多偏移N)
题目:(GDKOI 2014 day1)

(N,M≤100000)
每一次偏移,某个数的次数发生变化,这里如果预处理以每个数为底的幂,偏移一个单位更新答案的复杂度是O(1)的。
所以总的时间复杂度为O( (N+M) [√N ] )。
二、树上的分块
如何把在序列上的分块推广到树的路径查询问题上?
用dfs序!
把点i的“进入时间”记为pre[i],“离开时间”记为post[i]。
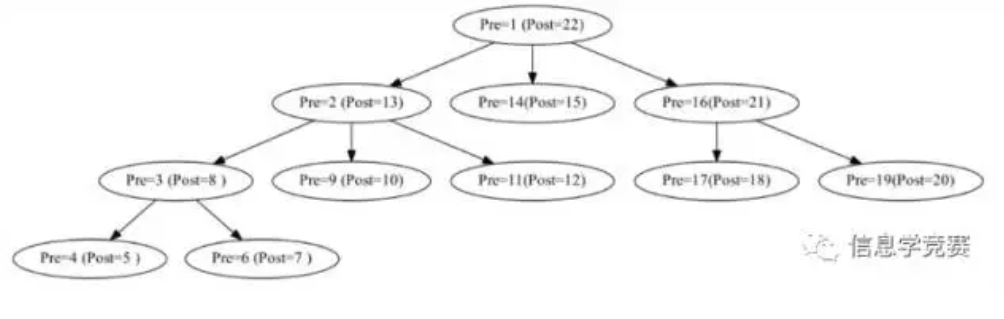
按照[ pre[x] / [√N ] ]为第一关键字,pre[y]作为第二关键字对查询的路径乱点(x,y)排序。
那么从路径(x, y)偏移到路径(x’, y’)也可以用类似的方法。每次暴力把x移动到x’,把y移动到y’。由于两点在树上的距离不会超过它们“进入时间戳pre”的差,所以同样可以用“一”中的分析得出一样的复杂度。
不同的是,把x偏移到x’, y偏移到y’时,为了实现简单,对经过的每个点都要判断是否会对答案有贡献。我们用state[i]表示i是否对答案有贡献(有则为1,没有则为0)。本来x到y路径上的点的state为1,现在要变成x’到y’路径上的点的state为1。对经过每个点i,如果它目前的state和目标的不一样(通过检查点i是否在x’到y’的路径上来判断),那么点i就要“加入/删除”我们的考虑范围,然后更新答案。
(当然,关于如何偏移和更新答案,也有其他的实现方法)
题目:SPOJ Count on a tree II
有一个 N 个结点的树,每个点上有整数点权。 M 个询问。询问 (u, v):求树上从 u 到 v 的路径上有几种不同的点权。
(N ≤ 40000, M ≤ 100000)
直接套用上面的方法,用一个桶(要先对点权离散化)记录每种点权的出现次数即可。
程序:
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cstdlib>
#include <cmath>
using namespace std;
#define maxN 40050
#define maxM 100050
int N, M, a[maxN], s[maxN], state[maxN], tot[maxN];
int now, H[maxN], fa[maxN], f[maxN][18];
int st[maxN], en[maxN], nowT;
struct Tdata
{
int id, nxt;
} edge[maxN * 2];
struct Topt
{
int u, v;
int st1, st2;
int id;
} opt[maxM];
int len;
int res[maxM], ans;
void addedge(int a, int b)
{
++ now;
edge[now].id = b;
edge[now].nxt = H[a];
H[a] = now;
}
void dfs()
{
static struct Tstack {int now, tmp;} stk[maxN];
nowT = 0;
int top = 1;
stk[1].now = 1;
stk[1].tmp = H[1];
fa[1] = 1;
while (top)
{
int now = stk[top].now;
int &tmp = stk[top].tmp;
if (tmp == H[now])
{
st[now] = ++ nowT;
}
if (tmp && edge[tmp].id == fa[now]) tmp = edge[tmp].nxt;
if (!tmp)
{
en[now] = ++ nowT;
-- top;
continue;
}
int id = edge[tmp].id;
fa[id] = now;
tmp = edge[tmp].nxt;
++ top;
stk[top].now = id;
stk[top].tmp = H[id];
}
}
int Asklca(int x, int y)
{
if (x == y) return x;
if (st[x] > st[y]) swap(x, y);
for (int i = 16; i >= 0; --i)
if (st[ f[y][i] ] > st[x]) y = f[y][i];
return fa[y];
}
bool cmp(const Topt &A, const Topt &B)
{
int g1 = A.st1 / len, g2 = B.st1 / len;
return g1 < g2 || (g1 == g2 && A.st2 < B.st2);
}
#define IsAnc(anc, a) (st[anc] <= st[a] && en[a] <= en[anc])
#define OnPath(a, u, v, lca) (IsAnc(lca, a) && ( IsAnc(a, u) || IsAnc(a, v) ) )
void Change(int x)
{
if (state[x] == 1) ans -= ( (-- tot[ a[x] ] == 0));
else ans += ( ( tot[ a[x] ] ++ )==0 );
state[x] ^= 1;
}
void Move(int a, int b, int u, int v, int w)
{
int t = Asklca(a, b);
for (; a != t; a = fa[a])
if (OnPath(a, u, v, w) != state[a]) Change(a);
for (; b != t; b = fa[b])
if (OnPath(b, u, v, w) != state[b]) Change(b);
if (OnPath(t, u, v, w) != state[t]) Change(t);
}
int main()
{
freopen("input.txt", "r", stdin);
freopen("output.txt", "w", stdout);
scanf("%d%d", &N, &M);
for (int i = 1; i <= N; ++i) scanf("%d", a+i);
for (int i = 1; i < N; ++i)
{
int u, v;
scanf("%d%d", &u, &v);
addedge(u, v);
addedge(v, u);
}
dfs();
for (int i = 1; i <= N; ++i) f[i][0] = fa[i];
for (int j = 1; j <= 16; ++j)
for (int i = 1; i <= N; ++i)
f[i][j] = f[ f[i][j-1] ][j-1];
for (int i =1; i <= M; ++i)
{
scanf("%d%d", &opt[i].u, &opt[i].v);
if (st[opt[i].u] > st[opt[i].v]) swap(opt[i].u, opt[i].v);
opt[i].st1 = st[ opt[i].u ];
opt[i].st2 = st[ opt[i].v ];
opt[i].id = i;
}
len = sqrt( (int) (nowT + 0.5) );
sort(opt+1, opt+M+1, cmp);
for (int i = 1; i <= N; ++i) s[i] = a[i];
sort(s+1, s+N+1);
for (int i = 1; i <= N; ++i)
a[i] = lower_bound(s+1, s+N+1, a[i]) - s;
memset(state, 0, sizeof(state));
int lastu = 1, lastv = 1;
ans = 0;
for (int i = 1; i <= M; ++i)
{
int u = opt[i].u, v = opt[i].v, lca = Asklca(u, v);
Move(lastu, u, u, v, lca);
Move(lastv, v, u, v, lca);
lastu = u;
lastv = v;
res[ opt[i].id ] = ans;
}
for (int i = 1; i <= M; ++i) printf("%d\n", res[i]);
return 0;
}
NOIP信息学视频地址
视频地址
链接:https://pan.baidu.com/s/1tHo1DFMaDuMZAemNH60dmw
提取码:7jgr


