NOIP--图论习题讲解
例题3-1:农场网络
【问题描述】Bessie受雇来到John的农场帮他们建立internet网络。农场有 N (2<= N <= 1,000)牛棚,编号为1..N。John之前已经勘测过,发现有 M (1<= M <= 20,000)条可能的连接线路,一条线路是连接某两个牛棚的。每条可能的线路都有一个建设费用 C (1<= C <=100,000)。John当然想花尽量少的钱,甚至克扣Bessie的工钱。
Bessie发现了这点,很生气,决定给John捣乱。她要选择一些线路组成网,但费用却尽可能大。当然网络要能正常工作,也就是任意两个牛棚之间都是相互可以连通的,并且网络上不能有环,不然John会很容易发现的。请计算组建这种网络最多可能的费用。
【分析】本题题目中说网络上不能有环,那么该网络就是一棵树。又题目中要求使得费用尽可能多,因此本题策略即为求解最大生成树。最大生成树与最小生成树方法类似,都用Kruskal算法执行,仅仅边的排序顺序不同。
例题3-2:最优贸易(NOIP2009)【问题描述】C国有n个大城市和m条道路,每条道路连接这n个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这m条道路中有一部分为单向通行的道路,一部分为双向通行的道路,双向通行的道路在统计条数时也计为1条。C国幅员辽阔,各地的资源分布情况各不相同,这就导致了同一种商品在不同城市的价格不一定相同。但是,同一种商品在同一个城市的买入价和卖出价始终是相同的。
商人阿龙来到C国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息之后,便决定在旅游的同时,利用商品在不同城市中的差价赚回一点旅费。设C国n个城市的标号从1~n,阿龙决定从1号城市出发,并最终在n号城市结束自己的旅行。在旅游的过程中,任何城市可以重复经过多次,但不要求经过所有n个城市。阿龙通过这样的贸易方式赚取旅费:他会选择一个经过的城市买入他最喜欢的商品——水晶球,并在之后经过的另一个城市卖出这个水晶球,用赚取的差价当做旅费。由于阿龙主要是来C国旅游,他决定这个贸易只进行最多一次,当然,在赚不到差价的情况下他就无需进行贸易。假设C国有5个大城市,城市的编号和道路连接情况如下图,单向箭头表示这条道路为单向通行,双向箭头表示这条道路为双向通行。
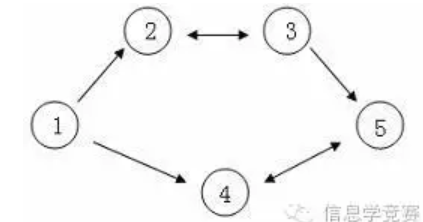
假设1~n号城市的水晶球价格分别为4,3,5,6,1。阿龙可以选择如下一条线路:1->2->3->5,并在2号城市以3的价格买入水晶球,在3号城市以5的价格卖出水晶球,赚取的旅费数为2。
阿龙也可以选择如下一条线路1->4->5->4->5,并在第1次到达5号城市时以1的价格买入水晶球,在第2次到达4号城市时以6的价格卖出水晶球,赚取的旅费数为5。
现在给出n个城市的水晶球价格,m条道路的信息(每条道路所连接的两个城市的编号以及该条道路的通行情况)。请你告诉阿龙,他最多能赚取多少旅费。
【输入】第一行包含2个正整数n和m,中间用一个空格隔开,分别表示城市的数目和道路的数目。
第二行n个正整数,每两个整数之间用一个空格隔开,按标号顺序分别表示这n个城市的商品价格。
接下来m行,每行有3个正整数,x,y,z,每两个整数之间用一个空格隔开。如果z=1,表示这条道路是城市x到城市y之间的单向道路;如果z=2,表示这条道路为城市x和城市y之间的双向道路。
【输出】共1行,包含1个整数,表示最多能赚取的旅费。如果没有进行贸易,则输出0。
【样例输入】5 5
4 3 5 6 1
1 2 1
1 4 1
2 3 2
3 5 1
4 5 2
【样例输出】5
【说明】输入数据保证1号城市可以到达n号城市。
对于10%的数据,1≤n≤6。对于30%的数据,1≤n≤100。
对于50%的数据,不存在一条旅游路线,可以从一个城市出发,再回到这个城市。
对于100%的数据,1≤n≤100000,1≤m≤500000,1≤x,y≤n,1≤z≤2,1≤各城市水晶球价格≤100。
【分析】本题思路比较简单,很直观的就是想找到一个价格最低和一个价格最高点(满足由起点能到达最低点,最低点能到达最高点,且最高点又能到达终点)。由于n较大,如果直接枚举,必然超时。
我们不妨先只考虑问题的一半,即找到从起点到任意节点路径上最低价格。显然,这与最短路径的求解方式一致,不同的只是更新函数修改
由于本题中有环,因此需要用SPFA来实现。
对于问题的另一半,即找到从任意节点到终点路径上的最高价格,与前一半问题类似。我们只需将所有边反向,问题即变成求解终点到任意节点路径上的最高价格。
综上,只需要用SPFA求解所有点与起点路径上的最低价格,再将原图边反向,求解所有点与终点路径上的最高价格;然后枚举中间点,找到差价最大的节点。如果差价大于1,则输出差价,否则输出0。
例题3-3:奶牛分配
【问题描述】农夫约翰上个星期刚刚建好了他的新牛棚,他使用了最新的挤奶技术。不幸的是,由于工程问题,每个牛栏都不一样。第一个星期,农夫约翰随便地让奶牛们进入牛栏,但是问题很快地显露出来:每头奶牛都只愿意在她们喜欢的那些牛栏中产奶。上个星期,农夫约翰刚刚收集到了奶牛们的爱好的信息(每头奶牛喜欢在哪些牛栏产奶)。一个牛栏只能容纳一头奶牛,当然,一头奶牛只能在一个牛栏中产奶。给出奶牛们的爱好的信息,计算最大分配方案。
【分析】本题为经典二分图匹配问题。奶牛与牛栏为两个类别,如果一头奶牛愿意在某个牛栏中产奶,则在这两个节点之间连边。最后,求解二分图的最大匹配即可。
NOIP信息学视频地址
视频地址
链接:https://pan.baidu.com/s/1tHo1DFMaDuMZAemNH60dmw
提取码:7jgr


