NOIP--数据结构与图论-习题详解(树,二叉树,堆)
1. 例题解析:
例题2-1:树网的核(NOIP2007)
【问题描述】设T=(V, E, W) 是一个无圈且连通的无向图(也称为无根树),每条边到有正整数的权,我们称T为树网(treebetwork),其中V,E分别表示结点与边的集合,W表示各边长度的集合,并设T有n个结点。
路径:树网中任何两结点a,b都存在唯一的一条简单路径,用d(a, b)表示以a, b为端点的路径的长度,它是该路径上各边长度之和。我们称d(a, b)为a, b两结点间的距离。
D(v, P)=min{d(v,u), u为路径P上的结点}。
树网的直径:树网中最长的路径成为树网的直径。对于给定的树网T,直径不一定是唯一的,但可以证明:各直径的中点(不一定恰好是某个结点,可能在某条边的内部)是唯一的,我们称该点为树网的中心。
偏心距ECC(F):树网T中距路径F最远的结点到路径F的距离,即
ECC(F)=max{d(v,F),v∈V}
任务:对于给定的树网T=(V, E, W)和非负整数s,求一个路径F,他是某直径上的一段路径(该路径两端均为树网中的结点),其长度不超过s(可以等于s),使偏心距ECC(F)最小。我们称这个路径为树网T=(V,E, W)的核(Core)。必要时,F可以退化为某个结点。一般来说,在上述定义下,核不一定只有一个,但最小偏心距是唯一的。
下面的图给出了树网的一个实例。图中,A-B与A-C是两条直径,长度均为20。点W是树网的中心,EF边的长度为5。如果指定s=11,则树网的核为路径DEFG(也可以取为路径DEF),偏心距为8。如果指定s=0(或s=1、s=2),则树网的核为结点F,偏心距为12。
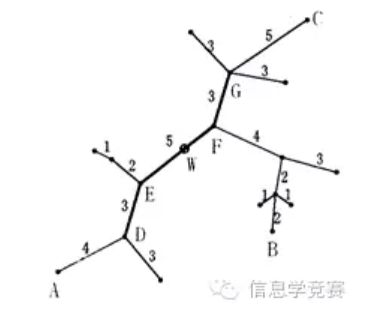
【输入】输入第1行,两个正整数n和s,中间用一个空格隔开。其中n为树网结点的个数,s为树网的核的长度的上界。设结点编号以此为1,2,……,n。
从第2行到第n行,每行给出3个用空格隔开的正整数,依次表示每一条边的两个端点编号和长度。例如,“24 7”表示连接结点2与4的边的长度为7。
所给的数据都是正确的,不必检验。
【输出】输出只有一个非负整数,为指定意义下的最小偏心距。
【样例输入】
5 2
1 2 5
2 3 2
2 4 4
2 5 3
【样例输出】
5
【说明】
40%的数据满足:5<=n<=15
70%的数据满足:5<=n<=80
100%的数据满足:5<=n<=300,0<=s<=1000。边长度为不超过1000的正整数
【分析】对于该问题,即求解一条边上的一个点,使得这个点到所有点的距离最大值最短。因此,我们可以枚举一条边,以这条边的端点为树根,建立两棵子树,计算子树中与根节点最远的节点的距离,最后计算出偏心距。令边x连接节点i和j,边x的长度为len[x],则:
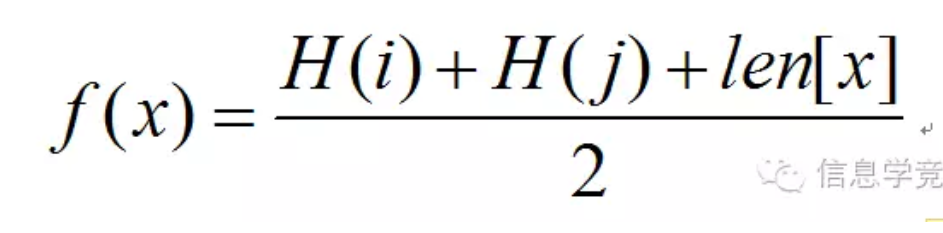
计算一棵树中与根节点最远的节点的距离,可用后根遍历方式,遍历到节点k时,
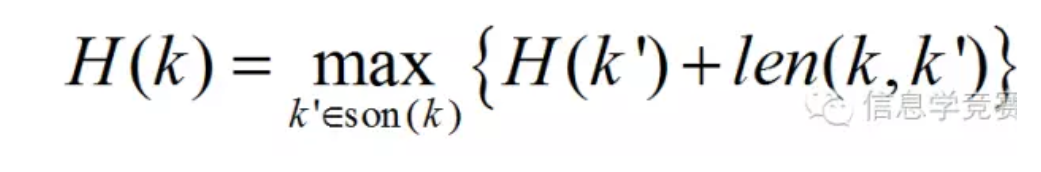
综上,枚举需要O(n)次,计算距离需要O(n)次,整体复杂度为O(n2)。
例题2-2:求第k大的数
【问题描述】在上课的时候,老师讲了一下求第k大的数的线性解法。小明觉得这个算法好厉害,但是想了一下,如果这些数字是依次输入,然后需要在任意时刻输出当前数组第k大的数,那该怎么办呢。于是他就想到了你,让你编程来完成上述操作。
程序有如下两种操作:
(1)添加一个数到数组中
(2)查询当前数组中第k大的数
【输入】第一行为n, k(n为操作数目,k为题目中的k值,n<=100000)
第二行到第n+1行,每一行有两种情况,如果是数字,则表示添加该数字到数组,如果是字符‘Q’,则表示查询第k大的数。
【输出】对于所有查询操作,输出对应的值,用空行分开。
【样例输入】
10 3
1
5
3
Q
8
4
Q
9
2
Q
【样例输出】
1
4
5
【分析】本题为堆的一个应用。由于本题中需要维护第k大的值,可建立一个大小为k的小根堆。当堆中元素个数不满k个时,在插入元素时,直接将其插入堆并调整即可;当堆中元素等于k个时,在插入元素时,判断与堆顶元素的大小,若大于堆顶元素,则替换堆顶元素,并调整。查找时,直接输出堆顶元素。
时间复杂度为O(N log K)。
NOIP信息学视频地址
视频地址
链接:https://pan.baidu.com/s/1tHo1DFMaDuMZAemNH60dmw
提取码:7jgr


