NOIP--数据结构与图论--树、二叉树、堆

树是包含n（n>0）个结点的有穷集合K，且在K中定义了一个关系N，N满足 以下条件：1) 有且仅有一个结点 K0，他对于关系N来说没有前驱，称K0为树的根结点。简称为根（root）。2) 除K0外，K中的每个结点，对于关系N来说有且仅有一个前驱。    （1）K中各结点，对关系N来说可以有m个后继（m>=0）。      通俗的来说，除了根节点，树结构当中所有其他节点均有一个前驱和若干个后继。

2.知识点梳理

2.1 树的概念、存储和遍历    树的概念一般描述在概述中已说明，通俗的定义和存储方式如下图所示：

 

 

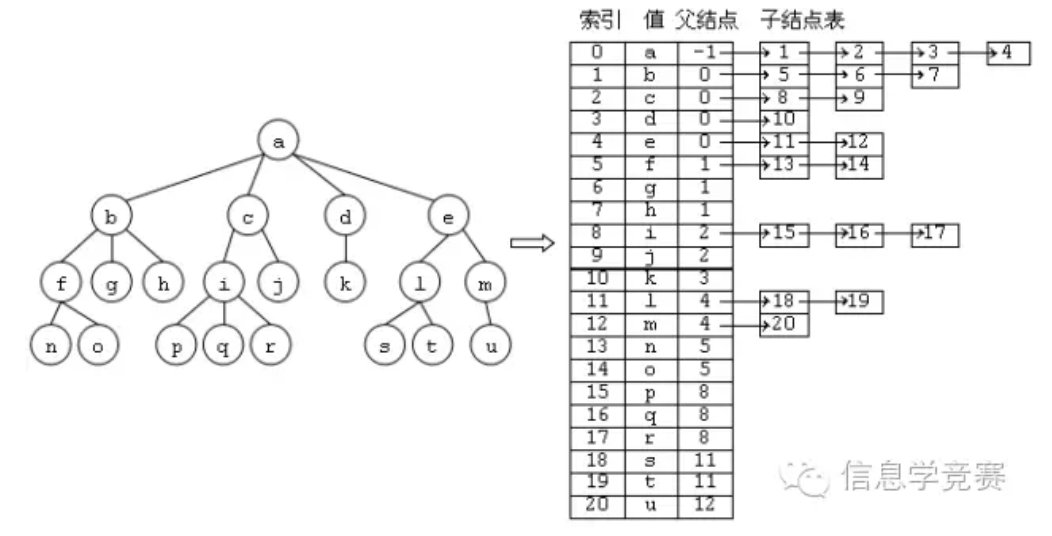
其中左图为一个显示表现形式，右图为存储方式。如果对链表不熟悉，也可以用数组模拟链表对树的子节点进行存储。        

树的遍历方式大致有三种：先根遍历、后根遍历和分层遍历。先根遍历即优先遍历根，然后再进行各个子树的遍历；后根遍历即优先遍历各个子树，最后遍历根；分层遍历即逐层扫描这棵树，一般用于宽度优先搜索。        

上述左图的先根遍历结果为abfnoghcipqrjdkelstmu，后根遍历结果为nofghbpqrijckdstlumea，分层遍历结果为abcdefghijklmnopqrstu。

2.2  二叉树和树的“左儿子右兄弟”表示法        

当树的所有节点的子节点个数小于等于2时，则称其为二叉树。二叉树由于其子树节点最多为两个，可将这两个节点分别称为左子树和右子树。        

二叉树的遍历除了数的通用的三种遍历方式外，还有一种遍历方式，称作“中序遍历”，即先左子树再根再右子树的遍历。另外，原先根遍历与后根遍历在二叉树中被称作先序遍历和后序遍历。        

对于一棵深度为k的二叉树，如果除最后一层无任何子节点外，每一层上的所有结点都有两个子结点，则称其为满二叉树，如下图。

 

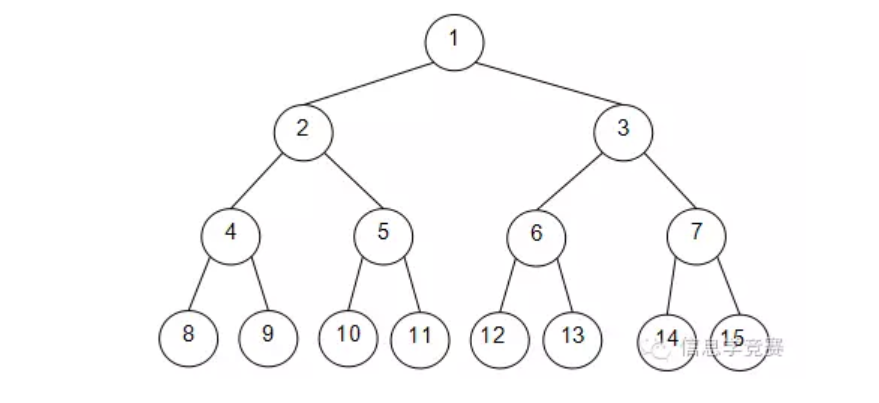
 完全二叉树是由满二叉树而引出来的。对于深度为k的，有n个结点的二叉树，当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树，如下图。

 

 

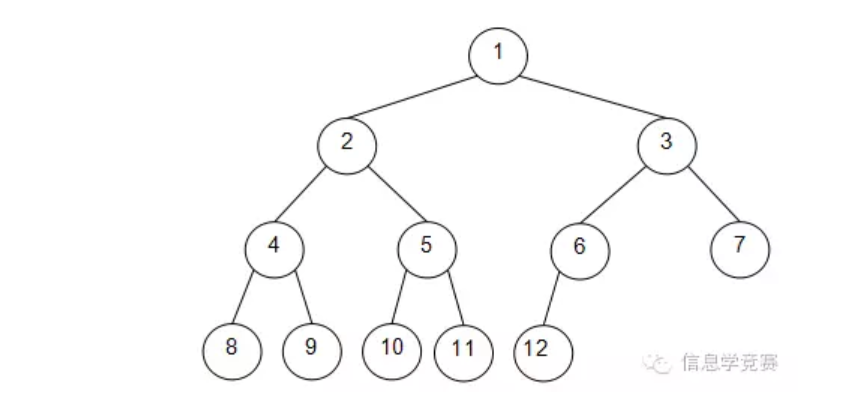
 在完全二叉树中，对于节点i，两个可能的子节点编号为i*2和i*2+1，父节点编号为i\2（整除）。

一般的树结构，可以转化为二叉树的形式保存。对于每个节点，左子树保存它的第一个子节点，右子树保存它右侧最近的兄弟节点，如下图。树的后根遍历对应其二叉树形式的中序遍历

 

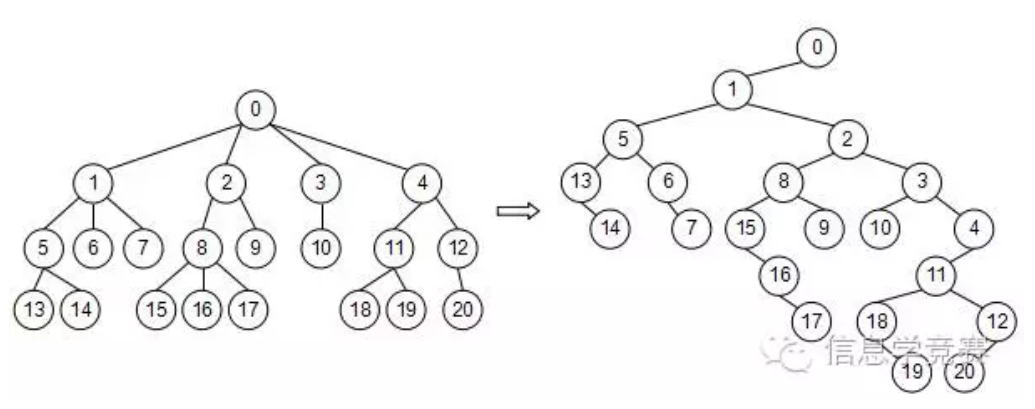
 2.3 堆       

 堆，是优先队列的一种实现形式，其本质就是满足特定条件的完全二叉树。对于一个特定的估价函数，堆中节点k的函数值大于等于其子节点函数值。       

 通常来说，堆有两种形式，一种是大根堆（节点值大于等于子节点值）和小根堆（节点值小于等于子节点值），实质这些只是估价函数的一种具体形式。现以大根堆来解释堆的一些基本操作。       

 插入元素：将元素放到堆的末尾，判断该元素与其父节点元素之间的大小，若大于其父节点的值，则交换，继续向上。

删除顶元素：顶元素删除后，将堆末尾的元素放至顶端，判断该元素与其两个子节点之间的大小，若子节点的值大于该节点的值，则与较大的那个子交换，继续向下调整。

删除任意元素：任意位置元素删除后，将堆末尾的元素放至该位置，向上调整至无法调整，再向下调整至无法调整。        

建堆：从前往后扫描，所有节点向上调整一次即可。        

堆的应用主要有堆排序、A*搜索（搜索算法中搜索顺序的确定）、图的最小生成树Kruskal算法等。

 

NOIP信息学视频地址

视频地址

链接：https://pan.baidu.com/s/1tHo1DFMaDuMZAemNH60dmw 
提取码：7jgr