NOIP--数据结构与图论-基本数据结构
数据结构是计算机存储、组织数据的方式,指的是相互之间存在一种或多种特定关系的数据元素的集合。其操作一般包括插入、删除、查找、统计等。根据数据关系的不同,一般分为线性结构、集合、树形结构、图形结构四种。其中,线性结构和集合是比较基础的数据结构。
1. 知识点梳理:
Ø 线性表、栈和队列
线性表是最基础的线性数据结构。包含两种存储方式:一种是顺序存储,另一种是链式存储。前者只需用一维数组实现,而后者既可以用数组实现,又可以用指针实现。栈是只能在某一端插入和删除的特殊线性表。它按照先进后出的原则存储数据,先进入的数据被压入栈底,最后的数据在栈顶,需要读数据的时候从栈顶开始弹出数据。栈是按照“先进后出”的原则组织数据的。
队列也是一种特殊的线性表,它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作。进行插入操作的端称为队尾,进行删除操作的端称为队头。队列是按照“先进先出”的原则组织数据的。
Ø 集合与并查集
集合是另一种形式的数据结构,指的是具有某种特定性质的事物的总体。集合中的元素无顺序性。其基本操作有:判断两个元素是否在同一集合、合并两个集合等。并查集是在只有上述两种基本操作时所衍生出的一种具体的数据结构。
并查集是以一种类似树形结构存储的数据结构,其节点保存它所在子树的父节点。具体执行的过程中,首先将所有元素的父节点设为自己,即F[i]=i。我们定义一个函数find(i)表示找到i集合所在的标记元素:
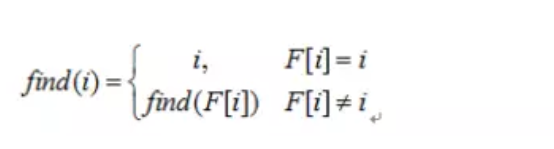
在递归的过程中,所有路径上的节点的父节点都设为集合的标记元素,伪代码为:
int find(i)
{
if (F[i]=i)
return i;
else
{
F[i]=find(F[i]);
return
F[i];
}
}
查找i,j节点是否在同一集合中,只要查看i和j节点所在集合的代表元素是否一致,即判断find(i)是否等于find(j).
合并i,j节点时,找到i和j节点所在集合的代表元素(即树根),并将两者进行合并,即:F[find(j)] = find(i);
Ø 散列(Hash)表
散列表(Hash table,也叫哈希表),是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
举个例子,给定N个整数,(N≤10000),整数的取值范围为0~109,判断有没有两个整数相等。在基础算法中讲过,如果进行比较,需要O(N log N)次比较,如果进行类似桶排序的操作,虽然时间复杂度为O(N),但是空间复杂度与数据取值范围相关。因此,需要找到一个映射,使得空间复杂度也大约为O(N)。散列函数即为此类映射。一种简单的散列函数为f(x) = x mod N,这样,将数据压缩到0~N-1的范围内,但有可能会有重复。通常来讲,用略大于N的素数整除取余数,会减少重复可能性。
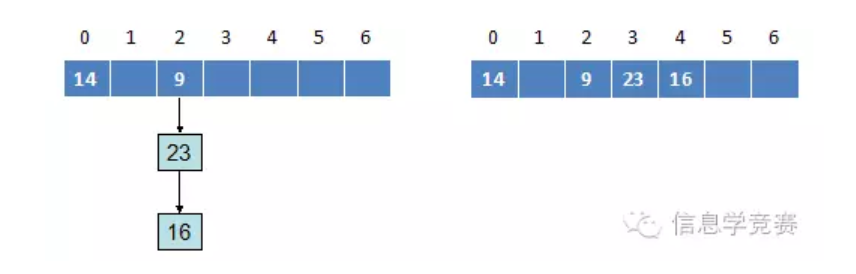
当数据出现重复时,有两种处理方式,一种是开散列方式,即在该节点生成一个链表,存储当前数据;另一种是闭散列方式,即使用其他散列函数,直至没有重复位置(一般向后扫描,找到一个没有重复的即可)。举个例子,当N=7时,插入元素14,9,23,16,对于开散列和闭散列,结果如下图,其中左图为开散列结果,右图为闭散列结果。
2.1.重难点分析:
v 线性表、栈和队列使用时,注意数组大小范围,如果用链表来模拟,注意指针使用。
v 并查集注意递归函数回溯过程中,将父节点标号更新。
v 散列表使用过程中,散列函数的挑选非常重要。
2.2.例题解析:
例题1-1:家族
【问题描述】某个家族人员过于庞大,要判断两个是否是亲戚,确实还很不容易,现在给出某个亲戚关系图,求任意给出的两个人是否具有亲戚关系。
规定:x和y是亲戚,y和z是亲戚,那么x和z也是亲戚。如果x,y是亲戚,那么x的亲戚都是y的亲戚,y的亲戚也都是x的亲戚。
【输入】第一行:三个整数n,m,p,(n<=5000,m<=5000,p<=5000),分别表示有n个人,m个亲戚关系,询问p对亲戚关系。
以下m行:每行两个数Mi,Mj,1<=Mi,Mj<=N,表示Ai和Bi具有亲戚关系。
接下来p行:每行两个数Pi,Pj,询问Pi和Pj是否具有亲戚关系。
【输出】 P行,每行一个‘Yes’或‘No’。表示第i个询问的答案为“具有”或“不具有”亲戚关系。
【分析】 本题为经典并查集问题。如果两个人有亲戚关系,则将两人所在集合合并。讯问时,判断两人是否在同一集合中即可。
例题1-2:团伙
【问题描述】某地的黑社会组织猖獗,警方经过长期的调查,初步获得了一些资料:整个组织有n个人,任何两个认识的人不是朋友就是敌人,而且满足:① 朋友的朋友是朋友;② 敌人的敌人是朋友。
所有是朋友的人组成一个团伙。现在,警方拥有关于这n个人的m条信息(即某两个人是朋友,或某两个人是敌人),请你计算出该地最多可能有多少个团伙。
【分析】 本题是并查集问题的拓展。对于朋友信息,很容易想到用并查集进行集合合并。但是对于敌人信息,不是很容易就能想到合并操作。事实上,对于每一个人k,记录这个人的反面k’,如果i,j两人是朋友,则将i,j合并,i’,j’合并;如果两人是敌人,则将i,j’合并,i’,j合并。最后除去只有反面的集合,统计剩余集合中正面的人物与集合数目即可。
例题1-3:关押罪犯(NOIP2010)
【问题描述】S 城现有两座监狱,一共关押着N (N≤20000) 名罪犯,编号分别为1~N。他们之间的关系自然也极不和谐。很多罪犯之间甚至积怨已久,如果客观条件具备则随时可能爆发冲突。我们用“怨气值”(一个正整数值)来表示某两名罪犯之间的仇恨程度,怨气值越大,则这两名罪犯之间的积怨越多。如果两名怨气值为c 的罪犯被关押在同一监狱,他们俩之间会发生摩擦,并造成影响力为c 的冲突事件。冲突的数目为M (M≤100000)。
每年年末,警察局会将本年内监狱中的所有冲突事件按影响力从大到小排成一个列表,然后上报到S 城Z 市长那里。公务繁忙的Z 市长只会去看列表中的第一个事件的影响力,如果影响很坏,他就会考虑撤换警察局长。
在详细考察了N 名罪犯间的矛盾关系后,警察局长觉得压力巨大。他准备将罪犯们在两座监狱内重新分配,以求产生的冲突事件影响力都较小,从而保住自己的乌纱帽。假设只要处于同一监狱内的某两个罪犯间有仇恨,那么他们一定会在每年的某个时候发生摩擦。那么,应如何分配罪犯,才能使Z 市长看到的那个冲突事件的影响力最小?这个最小值是多少?
【分析】 在“枚举”章节中,本题用次优的二分枚举解答。此题最优解法为并查集解法,在此做详细描述。
同上述团伙题目,记录每一个人k的反面k’,将冲突先是把怨气值从小到大排序一遍,然后从大到小枚举。对于一个i和j的怒气值为x的冲突,判断i和j是否在一个集合,如果在,则返回该怒气值;否则,将i和j’合并,j和i’合并。
排序时间复杂度为O(M log M),并查集时间复杂度为O(M),总体时间复杂度为O(M log M)。
NOIP信息学视频地址
视频地址
链接:https://pan.baidu.com/s/1tHo1DFMaDuMZAemNH60dmw
提取码:7jgr


