NOIP--搜索与动态规划-动态规划重难点习题详解
1. 动态规划习题讲解:
例题2-6:过河(NOIP2005)
【问题描述】在河上有一座独木桥,一只青蛙想沿着独木桥从河的一侧跳到另一侧。在桥上有一些石子,青蛙很讨厌踩在这些石子上。由于桥的长度和青蛙一次跳过的距离都是正整数,我们可以把独木桥上青蛙可能到达的点看成数轴上的一串整点:0, 1, ... , L(其中L是桥的长度)。坐标为0的点表示桥的起点,坐标为L的点表示桥的终点。青蛙从桥的起点开始,不停的向终点方向跳跃。一次跳跃的距离是S到T之间的任意正整数(包括S,T)。当青蛙跳到或跳过坐标为L的点时,就算青蛙已经跳出了独木桥。题目给出独木桥的长度L,青蛙跳跃的距离范围S,T,桥上石子的位置。你的任务是确定青蛙要想过河,最少需要踩到的石子数。
【输入】输入第一行有一个正整数L(1≤L≤109),表示独木桥的长度。第二行有三个正整数S,T,M,分别表示青蛙一次跳跃的最小距离,最大距离,及桥上石子的个数,其中1≤S≤T≤10,1≤M≤100。第三行有M个不同的正整数分别表示这M个石子在数轴上的位置(数据保证桥的起点和终点处没有石子)。所有相邻的整数之间用一个空格隔开。
【输出】输出只包括一个整数,表示青蛙过河最少需要踩到的石子数。
【分析】本题乍一看上去好像很简单,因为只要沿着青蛙跳的方向,逐步递推即可。用f(i)记录走到位置i时,最少踩到的石子数,状态转移方程为:
f(i) = min{f(j)}+a(i) 其中 i-T<=j<=i-S
时间复杂度为O(TL),空间复杂度为O(TL)。仔细观察题目,发现L的数字特别大,直接进行上述动态规划在时空间上都吃不消。
再次观察题目,发现S和T的值非常小,M的值也非常小,两颗石子之间有可能会有很大空隙,朴素动态规划在时间和空间上都很浪费。用石子作为阶段,石子前后若干空格作为状态,可将原状态修改为g(k,x),其中k为第k颗石子,x为与该石子距离为x的空格(-ST≤x≤ST)。那么,跳跃的过程即为从第k-1个石子的右边跳到第k个石子的左边,然后从第k个石子的左边,再跳到第k个石子的右边。状态转移函数为:
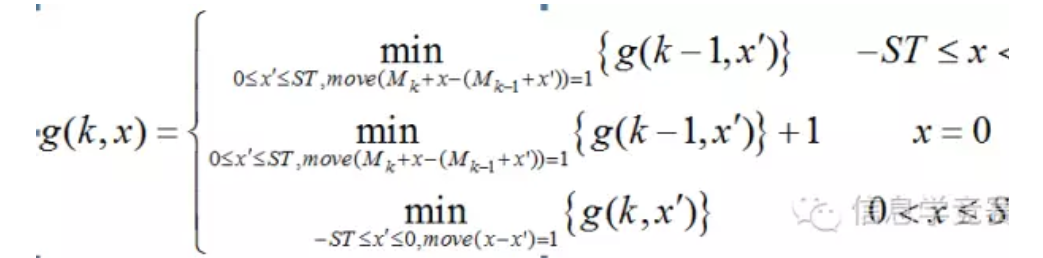
其中,move(x)表示青蛙是否可以跳x格空格(如果可以为1,否则为0),可以由S和T预处理。最终的解为最后一颗石子的右侧所有值中的最小值。
时间复杂度为O((ST)2M),空间复杂度为O(STM)。
例题2-7:01背包问题
【问题描述】有N件物品和一个容量为C的背包。第i件物品的重量是c[i],价值是w[i]。求解将哪些物品装入背包可使价值总和最大。
【分析】经典的背包问题。定义f(i,c)表示将前i个物品装入容量为c的背包中所获得的最大价值。状态转移方程为:
f(i,c) = max{f(i-1,c),f(i-1,c-w[i])+v[i]}
初值为f(0,c)=0(c=0...C),边界条件为f(i,c)=负无穷(c<0)。时间复杂度为O(NC),空间复杂度为O(NC)。
实际上,观察状态转移方程,f(i,c)的值只与f(i-1,c’)的值有关,因此,可用滚动数组压缩状态至2C。再次观察状态转移方程,发现c'<c,因此,如果从后往前扫描数组,可用一维数组维护,空间复杂度降为O(C)。伪代码如下:
For i=1 to n
For j=C downto 0
End For
End For

NOIP信息学视频地址
视频地址
链接:https://pan.baidu.com/s/1tHo1DFMaDuMZAemNH60dmw
提取码:7jgr


