NOIP--搜索与动态规划-搜索的重难点和例题解读
1. 搜索的重难点
Ø 题目的分析与搜索策略的选择。深度优先搜索和宽度优先搜索适合的题目类型不同。
Ø 搜索算法的完备性。搜索算法必须包含的最优解。
Ø 搜索算法的复杂度预测与算法优化。
2. 例题分析
例题1-1:N皇后问题
【问题描述】在国际象棋中,皇后可以攻击与她在同一条水平线、垂直线和对角线的棋子。现在有一张N×N的国际象棋棋盘,在上面放置N个皇后。问有多少种使皇后不能互相攻击的方案?(N≤13)
【分析】本题是一个经典的深度优先搜索题。由于皇后可以攻击同一水平线的棋子,要让皇后们互相攻击不到,每一行只有一个皇后。因此,搜索策略是,逐行搜索,枚举每一行皇后的位置,如果有皇后能
互相攻击到,则回溯,否则继续下一行。
本题如果不加优化,理论最坏时间复杂度为O(NN),但实际上达不到这个复杂度,但是也容易超时。下面说一些可行的优化。
依据对称性进行优化,对于第一行,只要枚举前N/2个点即可,根据左右对称特点,复制出右边的即可。可将时间消耗减少一半。
递归时记录下一行皇后的可能位置。在递归的过程中,每放置一个皇后,更新所有该皇后可以攻击到的区域;在回溯的过程中,将这些区域清空。
状态压缩。将每一行的状态记录在一个整形变量中,并且使用位运算——这样,速度会比朴素算法的快很多。
例题1-2:走迷宫
【问题描述】现有一个m行n列的迷宫 (m≤1000, n≤1000),其中白色(0)代表可以通过,黑色(1)代表不可通过(墙)。请给出任意一条从(1,1)出发到(m,n)的最短路径。如果不能到达,输出“Failed”。下图给出了一个迷宫样例。边给出输入样例,右边给出图示:
10 8
0001000000
0101011110
0111000100
0001010111
0100010001
0111011100
1101010101
0000010000
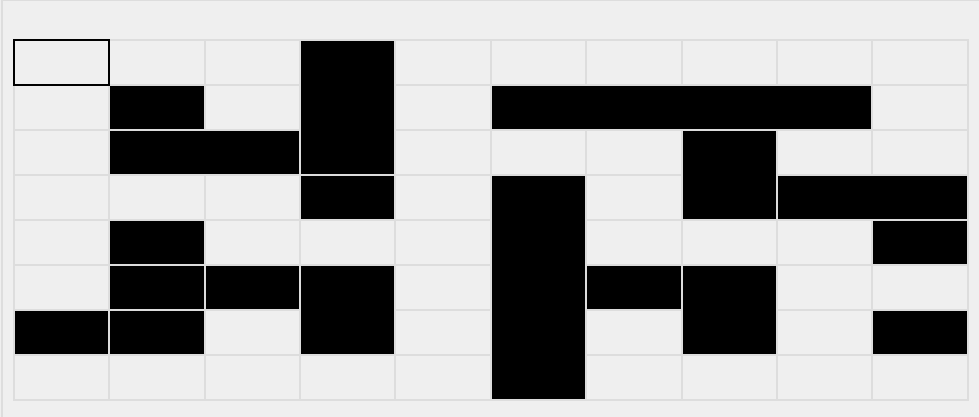
图中,蓝色箭头所示路径即为一条可行的最短路径。
【分析】本题为经典的宽度优先搜索题。对于本题,如果使用深度优先搜索,当m和n很大时,搜索深度会非常大,而且很多节点会被重复遍历。使用宽度优先搜索,记录该节点到根节点(1,1)的距离和该距离对应的上一步节点,按照与根节点的距离进行分层搜索。具体如下:
(1)将根节点加入队列,并将根节点状态更新为已遍历。
(2)如果队列为空,则输出Failed,程序结束,否则进入3。
(3)从队列中弹出一个节点,如果该节点为(m,n),则按照路径上节点记录的上一步节点,回溯得到路径,程序结束,否则进入4。
(4)判断它上下左右四个节点是否可行并未遍历。更新所有未遍历的可行节到根节点的距离为当前节点加一;更新所有未遍历的可行节点上一步节点为当前节点;将它们加入队列。进入2。
由于本题中所有节点只会被更新一次,因此,整个算法复杂度为O(mn)。该算法与漫水算法(FloodFill)类似。
例题1-3:字串变换(NOIP2002)
【问题描述】已知有两个字串 A$, B$ 及一组字串变换的规则(至多6个规则):
A1$ -> B1$
A2$ -> B2$
规则的含义为:在 A$ 中的子串 A1$ 可以变换为 B1$、A2$ 可以变换为B2$ …。
例如:A$='abcd',B$='xyz'
变换规则为:
‘abc’->‘xu’,‘ud’->‘y’,‘y’->‘yz’
则此时,A$ 可以经过一系列的变换变为B$,其变换的过程为:
‘abcd’->‘xud’->‘xy’->‘xyz’
共进行了三次变换,使得 A$ 变换为B$。
【输入】
第一行为两个字符串A$,B$。
从第二行开始若干行,每一行均为一个变换规则。A1$ B1$;A2$ B2$;...(所有字符串长度的上限为20)。
【输出】
若在 10 步(包含 10步)以内能将 A$ 变换为 B$ ,则输出最少的变换步数;否则输出"NOANSWER!"
【样例输入】
abcd wyz
abc xu
ud y
y yz
【样例输出】
3
【分析】本题可采用双向宽度优先搜索求解。本题给出了一个非常强的限定条件,即若在10步之内不能将 A$ 变换为 B$,则判断为无解。因此,利用宽度优先搜索,深度为10。题目中给出规则数为6,对于单向宽度优先搜索,状态数最多为610,有可能超时。
再看题目,由于变换是双向的,即如果 A$ 能够通过 Ai$ Bi$ 变换到 B$,那么 B$ 也可通过相应反变换变为 A$。因此,可采用双向宽度优先搜索。从 A$ 出发搜索5层,从 B$ 出发反向搜索5层,判断有无重复。这样状态数降至2*610,肯定不会超时。
例题1-4:Mayan游戏(NOIP2011)
【问题描述】
Mayan puzzle 是最近流行起来的一个游戏。游戏界面是一个7 行5 列的棋盘,上面堆放着一些方块,方块不能悬空堆放,即方块必须放在最下面一行,或者放在其他方块之上。游戏通关是指在规定的步数内消除所有的方块,消除方块的规则如下:
1、每步移动可以且仅可以沿横向(即向左或向右)拖动某一方块一格:当拖动这一方块时,如果拖动后到达的位置(以下称目标位置)也有方块,那么这两个方块将交换位置(参见输入输出样例说明中的图6 到图7);如果目标位置上没有方块,那么被拖动的方块将从原来的竖列中抽出,并从目标位置上掉落(直到不悬空,参见下面图1 和图2);
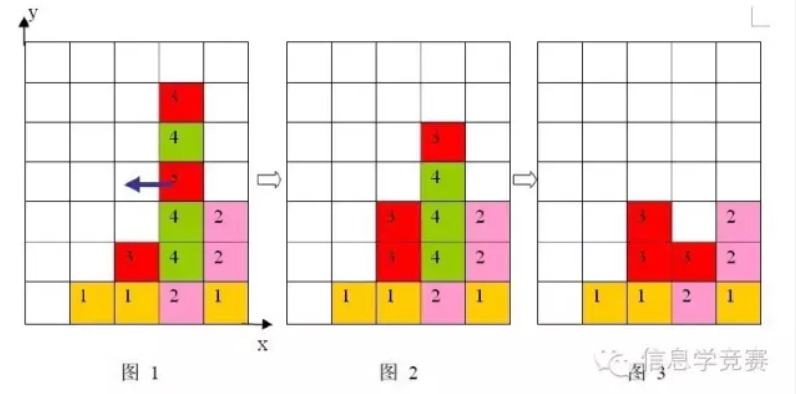
1、任一时刻,如果在一横行或者竖列上有连续三个或者三个以上相同颜色的方块,则它们将立即被消除(参见图1 到图3)。
注意:
a) 如果同时有多组方块满足消除条件,几组方块会同时被消除(例如下面图4,三个颜色为1 的方块和三个颜色为2 的方块会同时被消除,最后剩下一个颜色为2 的方块)。
b) 当出现行和列都满足消除条件且行列共享某个方块时,行和列上满足消除条件的所有方块会被同时消除(例如下面图5 所示的情形,5 个方块会同时被消除)。

1、方块消除之后,消除位置之上的方块将掉落,掉落后可能会引起新的方块消除。注意:掉落的过程中将不会有方块的消除。上面图 1 到图3 给出了在棋盘上移动一块方块之后棋盘的变化。棋盘的左下角方块的坐标为(0,0),将位于(3, 3)的方块向左移动之后,游戏界面从图1 变成图2 所示的状态,此时在一竖列上有连续三块颜色为4 的方块,满足消除条件,消除连续3 块颜色为4 的方块后,上方的颜色为3 的方块掉落,形成图3 所示的局面。
【输入】
输入共6 行。
第一行为一个正整数 n,表示要求游戏通关的步数。
接下来的 5 行,描述7*5 的游戏界面。每行若干个整数,每两个整数之间用一个空格隔开,每行以一个0 结束,自下向上表示每竖列方块的颜色编号(颜色不多于10 种,从1 开始顺序编号,相同数字表示相同颜色)。输入数据保证初始棋盘中没有可以消除的方块。
【输出】
如果有解决方案,输出n 行,每行包含3 个整数x,y,g,表示一次移动,每两个整数之间用一个空格隔开,其中(x,y)表示要移动的方块的坐标,g 表示移动的方向,1 表示向右移动,-1 表示向左移动。注意:多组解时,按照x 为第一关健字,y 为第二关健字,1优先于-1,给出一组字典序最小的解。游戏界面左下角的坐标为(0,0)。如果没有解决方案,输出一行,包含一个整数-1。
【样例输入】
3
1 0
2 1 0
2 3 4 0
3 1 0
2 4 3 4 0
【样例输出】
2 1 1
3 1 1
3 0 1
【样例说明】
按箭头方向的顺序分别为图 6 到图11
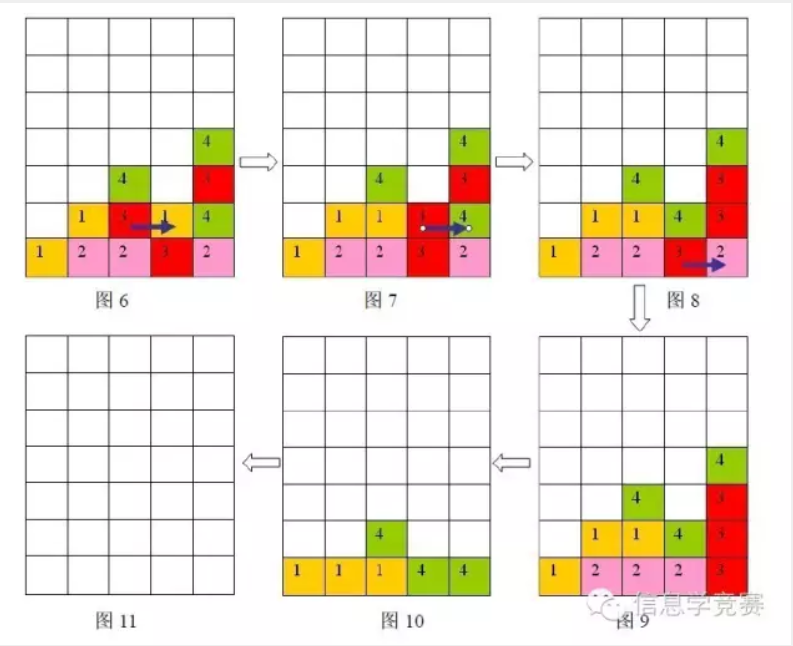
样例输入的游戏局面如上面第一个图片所示,依次移动的三步是:(2,1)处的方格向右移动,(3,1)处的方格向右移动,(3,0)处的方格向右移动,最后可以将棋盘上所有方块消除。
【数据范围】
对于 30%的数据,初始棋盘上的方块都在棋盘的最下面一行;
对于 100%的数据,0 < n≤5。
【分析】本题是一道比较复杂的搜索题。搜索时,按照字典序从小到大进行枚举,递归。本题的剪枝方案有:
(1) 搜索有层数限制,不用搜太多层
(2) 当左右两个点相同时,移动和不移动是一样的,则我们不用移动。
(3) 搜索每一个点,我们会发现将F[i,j]向右移和将F[i+1,j]向左移是一样的,则我们只搜索向右移的。
实际上,本题由于时限比较宽松,不用加太多优化就可以过,难点在于每一步枚举之后的状态更新较为繁琐,需注意。
NOIP信息学视频地址
视频地址
链接:https://pan.baidu.com/s/1tHo1DFMaDuMZAemNH60dmw
提取码:7jgr


