NOIP--基本算法设计-其他数学相关内容
其他相对比较常用的数学相关内容有:表达式求值、最大公约数与最小公倍数问题、质数与质因数分解问题等。
知识点梳理
Ø 表达式求值:
表达式求值,即用字符串给定一个表达式,然后求解表达式的值。表达式求解的方式大致有两种:一种为模拟,一种为分治。
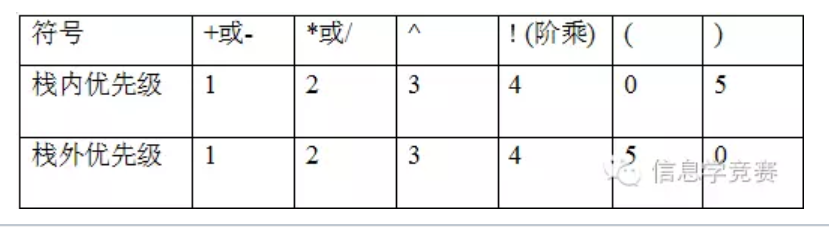
模拟法进行表达式求值时,建立两个栈,一个存放数值,一个存放运算符。扫描表达式,如果遇到数值,直接存入数值栈,遇到运算符,判断与栈顶运算符优先级,如果高于栈顶运算符,则存入运算符栈,否则,执行下面操作,直到当前运算符优先级高于栈顶运算符或栈为空。具体操作为:弹出当前栈顶运算符,并在数据栈中弹出相应数据(一般为两个,特殊情况如阶乘只有一个),做运算后,将运算结果存入数值栈。最后,依次弹出并执行运算符栈中的运算符,完成后,数据栈中仅存的数据,即为最终结果。需要注意的是,括号的栈外优先级和栈内优先级不同,一般运算优先级见下表。
分治法进行表达式求值时,对于表达式进行扫描,找出优先级最低的运算法,递归处理该运算符左右的表达式,然后进行该运算符的运算。
Ø 最大公约数与最小公倍数:
求解最大公约数用的是辗转相除法。用的依据是,如果正整数c是a和b的公约数,那么c也是b和a mod b的公约数。公式如下:

Ø 质数与质因数分解:
质数又称素数。指在一个大于1的自然数中,除了1和此整数自身外,不能被其他自然数整除的数。判断数k是否为质数,一般是扫描2到根号k内的整数,看是否能整除k,如果有,则k不是质数,否则k为质数。也可建立2到根号k的质数表用来扫描。找出区间2~n之间的所有质数,即建立2~n的质数表时,从小到大扫描,当遇到质数时,将其倍数删去,最后剩余的数即为质数表上的数。
质因数分解一般有两种方法:方法一:产生一个从2到根号k的质数表,然后从2开始除。在除干净之后换下一个因数。方法二:不产生质数表,直接从2开始除。在除干净之后换下一个因数。(注:n是素数时速度会非常慢)
重难点分析
2.1 表达式求值,需要先做出运算符优先级表,再进行代码编写。
2.2 表达式求值有时需要配合高精度,建议写成模块形式,方便操作。
2.3 表达式求值、最大公约数、质数问题等,基本只需要套用模板即可,平时注意整理此类模板,会省力很多。
例题解析例题3-1:等价表达式(NOIP2005)
【问题描述】明明进了中学之后,学到了代数表达式。有一天,他碰到一个很麻烦的选择题。这个题目的题干中首先给出了一个代数表达式,然后列出了若干选项,每个选项也是一个代数表达式,题目的要求是判断选项中哪些代数表达式是和题干中的表达式等价的。
这个题目手算很麻烦,因为明明对计算机编程很感兴趣,所以他想是不是可以用计算机来解决这个问题。假设你是明明,能完成这个任务吗?
这个选择题中的每个表达式都满足下面的性质:
1. 表达式只可能包含一个变量‘a’。
2. 表达式中出现的数都是正整数,而且都小于10000。
3. 表达式中可以包括四种运算‘+’(加),‘-’(减),‘*’(乘),‘^’(乘幂),以及小括号‘(’,‘)’。小括号的优先级最高,其次是‘^’,然后是‘*’,最后是‘+’和‘-’。‘+’和‘-’的优先级是相同的。相同优先级的运算从左到右进行。(注意:运算符‘+’,‘-’,‘*’,‘^’以及小括号‘(’,‘)’都是英文字符)
4. 幂指数只可能是1到10之间的正整数(包括1和10)。
5. 表达式内部,头部或者尾部都可能有一些多余的空格。
下面是一些合理的表达式的例子:
((a^1) ^ 2)^3,a*a+a-a,
((a+a)),
9999+(a-a)*a,
1 + (a -1)^3,
1^10^9,
……
【输入】输入的第一行给出的是题干中的表达式。第二行是一个整数n (2≤n≤26),表示选项的个数。后面n行,每行包括一个选项中的表达式。这n个选项的标号分别是A,B,C,D……输入中的表达式的长度都不超过50个字符,而且保证选项中总有表达式和题干中的表达式是等价的。
【输出】输出仅一行,这一行包括一系列选项的标号,表示哪些选项是和题干中的表达式等价的。选项的标号按照字母顺序排列,而且之间没有空格。
【样例输入】( a + 1) ^2
3
(a-1)^2+4*a
a + 1+ a
a^2 + 2 * a * 1 + 1^2 + 10 -10 +a -a
【样例输出】AC
【分析】这道题目拿到手后,一般可以想到的方法就是可不可以将所有的表达式全部转化为最简形式,这时,你就想到了一种一般的解决方案。即将所有的表达式全部化为最简,然后再计算,这种方法是一种准确的方法。但要在考场上实现,有一些麻烦,需要一些时间。这种方法的解决过程是:先将阶乘化乘,再展开。计算同时合并同类项,留下一个数组。然后比较每一个表达式的数组与题目数组是否相同,时间效率也并不高。那么怎么办呢?
我们这里介绍一种利用必要条件的解决方案。
即两个表达式如果等价,那么无论a为何值,两个表达式计算出的值都相等。这时,我们以不同的a值代入各式,可以快速排斥那些不同的表达式,留下的便是等价的了。我们怎样取值呢?
这里推荐几种有效的方法:
1)取随机函数生成的数列。这种方法比较有效,无规律。
2)取伪随机数列。这是一种比较便于人工控制的手段。
3)取实数。由于其他皆为整数,小数部分便成为判断的优越条件。对于1、2两种情况,有时表达式求解出的解会很大,应考虑对一个大素数取余数比较(由于没有除法,所以取余不会出错)。一般情况下取4~7组值便可通过极大部分情况。如果取更多组的值,便可以通过几乎所有的情况。
在上述分析完成后,剩下就是表达式求解的过程。可用模拟法或者分治法求解,此处略过。
例题3-2:Hankson的趣味题(NOIP2009)
【问题描述】Hanks博士是BT(Bio-Tech,生物技术)领域的知名专家,它的儿子明教Hankson。现在,刚刚放学回家的Hankson正在思考一个有趣的问题。
今天在课堂上,老师讲解了如何求两个正整数c1和c2的最大公约数和最小公倍数。现在Hankson认为自己已经熟练地掌握了这些知识,它开始思考一个“求公约数”和“求公倍数”之类问题的“逆问题”,这个问题是这样的:已经正整数a0, a1, b0, b1,设某未知正整数x满足:
1. x和a0的最大公约数为a1;
2. x和b0的最小公倍数为b1;
Hankson的“逆问题”就是求出满足条件的正整数x。但稍加思索后,它发现这样的x并不唯一,甚至可能不存在。因此他转而开始考虑如何求解满足条件的x的个数。请你帮助他编程求解这个问题。
【输入】第一行为正整数n,表示有n组数据。接下来,的n行,每行一组数据,为四个正整数a0, a1, b0, b1,每两个整数之间用一个空格隔开。输入数据保证a0能被a1整除,b1能被b0整除。
【输出】共n行。每行只有一个整数,即该组数据的结果。对于每组数据,输出满足条件的x的个数,若不存在这样的x,则输出0。
【样例输入】2
41 1 96 288
95 1 37 1776
【样例输出】
6
2
【分析】这道题的思路就是分解质因数。首先,不难得到gcd(x/a1,a0/a1)=1以及gcd(b1/x,b1/b0)=1。假设对于一个质因数y,a0含有a0c个y,a1含有a1c个y,b0含有b0c个y,b1含有b1c个y。那么不难得到,如果a0c<a1c,那么就无解;如果a0c=a1c,那么x至少含有a1c个y;如果a0c>a1c,那么x只可能含有a1c个y。同理,如果b1c<b0c,那么就无解;如果b1c=b0c,那么x至多含有b1c个y;如果b1c>b0c,那么x只可能含有b1c个y。由此,可以求出对于每一个质数,x可能含有几个它,并求出一共有多少种选择方式。然后根据乘法原理,将每一个质数的选择方案数乘起来,就得到了答案
NOIP信息学视频地址
视频地址
链接:https://pan.baidu.com/s/1tHo1DFMaDuMZAemNH60dmw
提取码:7jgr


