NOIP--基本算法设计-高精度算法与快速幂

1. 概述：

 

有的时候，数字会大到连long long（或int64）都不能承受的程度。这时，我们可以用数组来模拟大数的各种运算。该模拟方法即为高精度算法。

快速幂即为求解形如aⁿ的快速算法。

 

2. 知识点梳理：

 

Ø 高精度的存储

 

高精度存储采用数组存储每一位的值，并记录数组的长度和正负性。一般来讲，数组的下标越小，对应的整数的位越小。对于一个高精度整数n，用十进制计数后，其位数为k，每一位的值分别为a[0]~a[k-1]，那么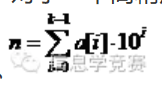

对于其他进制计数方式，只要改变底数即可。另外的，如果每一位只存储0~9，就比较浪费空间，而且增加计算复杂度常数。为了降低复杂度常数，就要进行所谓的压位存储（即每四位放到一个数中），其实就是相当于采用10000进制存储。

 

Ø 高精度的四则运算

 

加法：模拟整数加法的过程，从低位到高位逐位相加，判断进位即可。需要注意更新结果的位数，另外要注意负数情况。如果都为负，则相加后取负；如果只一个为负数，将其变成两数相减的形式。

减法：模拟整数减法的过程，从高位到低位逐位相减，不足从高位补即可。要更新结果的位数，另外要注意结果为负数。

乘法：模拟整数乘法的过程，依次两两相乘即可。对于10000进制存储的压位高精度，要注意在中间步骤进位，防止溢出。

除法：模拟整数除法的过程，从高位到低位逐位相除，最后可得出商和余数。在每一位相除的过程中，需要枚举该位的商。对于10000进制存储的压位高精度，直接枚举复杂度高，一般采用二分枚举。不过在NOIP中，高精度除法应用较少。

 

Ø 快速幂

一般求解aⁿ时，用依次相乘的方法即可，复杂度为O(n)，但实际上，如果记录a⁰, a¹, a², a⁴, a⁸, ... , 的值（其中），就可快速求解aⁿ，复杂度为O(log n)。如果直接求解，还需要用到高精度，复杂度会比较高。不过一般涉及到这类问题的题目，都要求计算出的解除以p取余数的结果。直接对每一步的计算结果取余数，就可以不用高精度计算。当然，快速幂的计算不仅仅限于计算一个值的幂，还可以用于递推下的矩阵计算。 

3. 重难点分析：

 

u 高精度算法中的正负号问题、升位与降位问题在运算中需要特别注意。

u 高精度算法在编写是容易出错，最好能准备一套模板。

u 快速幂求解时，应按照题目要求，看是否加入高精度。

 

4. 例题解析：

 

例题2-1：斐波那契数列第n项的值

【问题描述】计算斐波那契数列第n (n≤10¹⁰) 项的值。由于这个值会很大，只要计算其除以p的余数即可。

【分析】此题由于n非常大，直接一步步递推肯定超时，因此，需要利用快速幂的思想。已知斐波那契数列为

 

 例题2-2：2^k进制数（NOIP2006）

 

 

 

 

 

 

 

NOIP信息学视频地址

视频地址

链接：https://pan.baidu.com/s/1tHo1DFMaDuMZAemNH60dmw 
提取码：7jgr