NOIP--基本算法设计--分治算法
一、 分治
概述:
将一个难以直接解决的大问题,分割成若干规模较小的相同问题,通过对子问题的求解来得到原问题的解。这种算法设计策略叫做分治法。
1. 知识点梳理:
Ø 分治法的使用
分治法的使用基本是基于递归与回溯。先按照一定的分割方法,将原问题一步步分割为规模较小的子问题,递归调用求解子问题;然后在回溯时,利用子问题求解原问题的解。
Ø 用分治法解决的问题特点
分治法所能解决的问题一般具有以下几个特征:
1. 该问题的规模缩小到一定的程度就可以容易地解决。
2. 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质。
3. 利用该问题分解出的子问题的解可以合并为该问题的解。
4. 该问题所分解出的各个子问题是相互独立的,即子问题之间没有交集。
Ø 分治法相关的常用算法
分治法是一个非常实用的算法思想,在设计检索、分类算法或某些速算算法中很有效。用分治法思想的常用算法有二分枚举、二分检索、快速排序、归并排序等。
2. 重难点分析:
u 分治算法设计时,子问题之间必须独立。
u 分治算法设计时,应考虑其复杂度。有时会设计出复杂度跟直接求解一样的“伪分治法”。
u 分治法实现时,应注意递归调用时的边界条件。
3. 例题解析:
例题5-1:求逆序对个数
【问题描述】对于一个序列a1,a2,a3,…,an,如果存在i<j,使ai>aj,那么ai,aj就是一个逆序对。现在给你一个有N (N≤100000) 个元素的序列,请求出序列内逆序对的个数。

例题5-2:循环赛日程表问题
【问题描述】设有2n(n≤6)个球队进行单循环比赛,计划在2n-1天内完成,每个队每天进行一场比赛。设计一个比赛的安排,使在2n-1天内每个队都与不同的对手比赛。例如n=2时的比赛安排为:
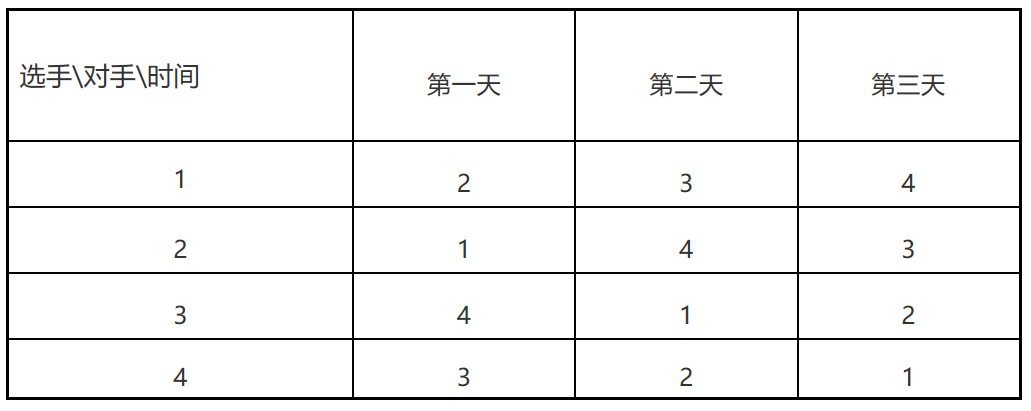
【分析】
此题很难直接给出结果,我们先将问题进行分解。
设m=2n,并将规模减半。假如n=3(即m=8),8个球队的比赛,减半后变成4个球队的比赛(m=4)。4个球队的比赛的安排方式还不是很明显,再减半到两个球队的比赛(m=2)。
两个球队的比赛安排方式很简单,只要让两个球队直接进行一场比赛即可:1-2
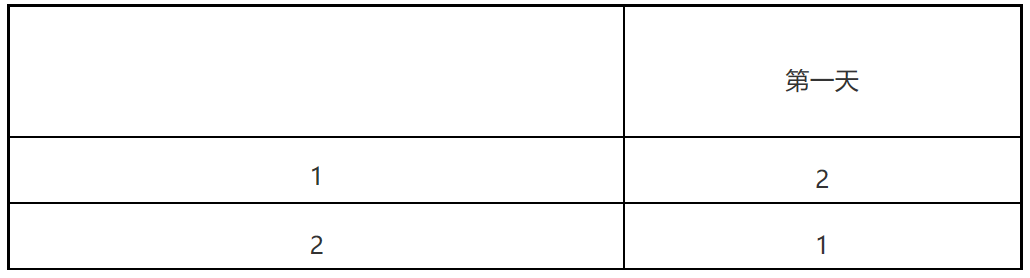
分析两个球队的比赛的情况不难发现,表格主体是一个对称的方阵,我们把这个方阵分成4部分(即左上、右上、左下、右下),右上部分可由左上部分加1(即加m/2)得到,而左上与右下部分、右上与左下部分分别相等。因此我们也可以把这个方阵看作是由m=1的方阵所生成的。同理,可得m=4的方阵:
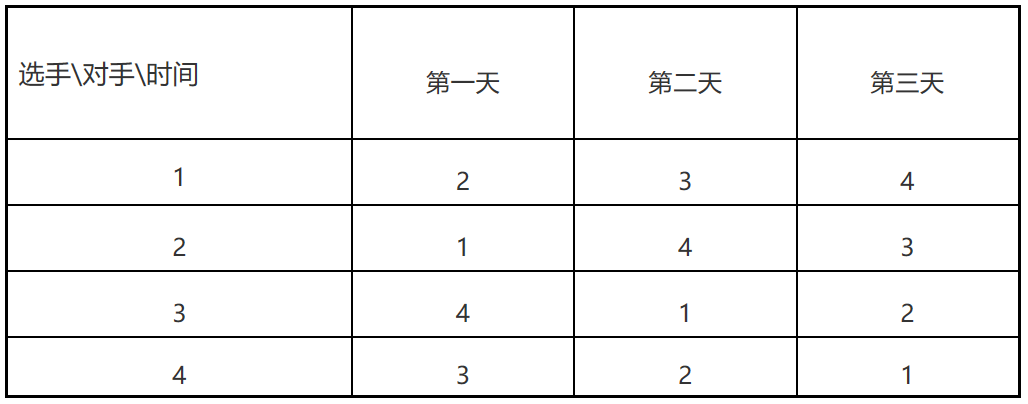
同理可由m=4方阵生成m=8的方阵:
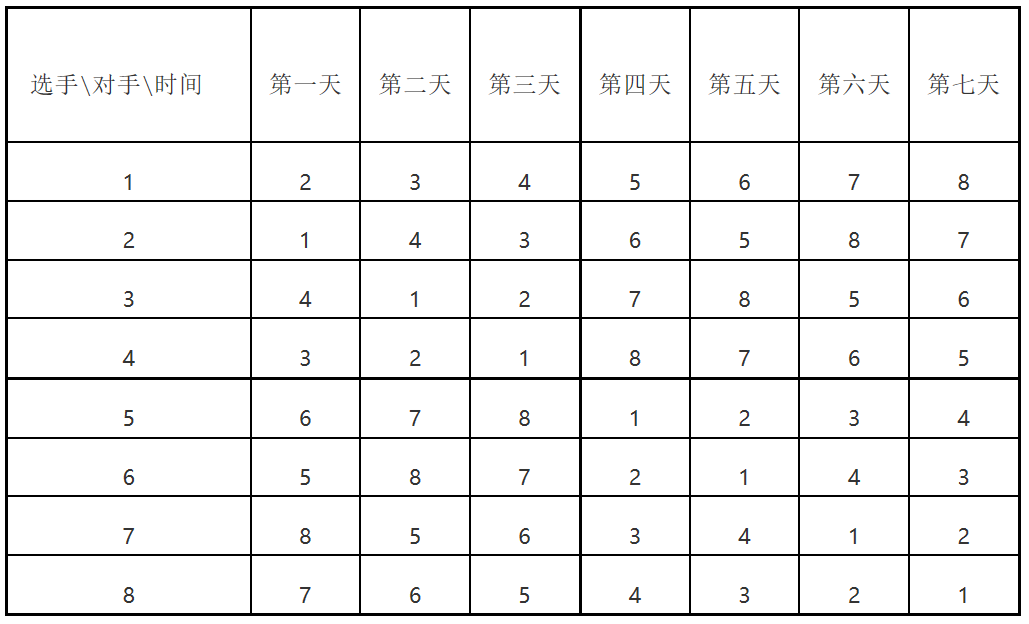
这样就构成了整个比赛的安排表。在算法设计中,用数组a记录2n个球队的循环比赛表,整个循环比赛表从最初的1×1方阵按上述规则生成2×2的方阵,再生成4×4的方阵……直到生成出整个循环比赛表为止。
NOIP信息学视频地址
视频地址
链接:https://pan.baidu.com/s/1tHo1DFMaDuMZAemNH60dmw
提取码:7jgr


