NOIP--递归与递推
递归与递推
1. 概述:
递归与递推是一些复杂算法的基础,其数据元素之间的关系可以用抽象的、严格的公式表达出来。递归与递推都具有边界条件,不同的是,递归从具体问题出发,一步步简化到边界条件;递推是从边界条件出发,一步步计算出具体问题。
2. 知识点梳理:
Ø 递归
递归,将具体问题用一些类似的子问题描述,最后用一定的边界条件进行约束。递归一般用函数自调用实线,当然,也可以用栈模拟函数调用来完成。递归是实现许多重要算法的基础。深度优先搜索、记忆化搜索、分治算法和输出动态规划的中间过程等都需要用递归实现。
Ø 递推
递推指利用其数据的前一项或几项,通过递推关系式来求出当前项的解。递推与递归不同,递推一般用循环语句完成,需要记录一定的中间结果。递推适合解决可用递推式计算的数学题,以及大部分动态规划题。
Ø 递归与递推的相关性
递推与递归之间也可以相互转化。当递归深度太深时,可尝试用递推解决。当递推顺序不明显的情况下,可利用递归和记忆化搜索的方式解决。递归结构清晰、可读性强、目的性强,但容易函数栈溢出或超时;递推速度较快、比较灵活,但有时思路不易想到。
3. 重难点分析:
u 递归算法在实现的过程中,要特别注意边界条件。没有边界条件会引发无限递归,从而导致程序崩溃。
u 递归算法深度过深时,应考虑用栈来模拟函数调用,避免系统栈溢出。
u 递归算法在执行过程中,应适当保留其中间结果,防止重复调用。
u 递推算法在执行过程中,其中间结果可能过多,应删去在之后递推中不会被用到的结果。
4. 例题解析:
【问题描述】已知有三根针分别用1、2、3表示。在一号针中从小到大放n个盘子,现要求把所有的盘子从1针全部移到3针。移动规则是:使用2针作为过渡针,每次只移动一块盘子,且每根针上不能出现大盘压小盘,找出移动次数最小的方案。
【分析】这是一个经典的递归问题。
递归的思路:如果想把n个盘子放到3针上,就应该先把n-1个盘子放到2针上。然后把1针最底部的盘子移动到3针,再把2针上的n-1个盘子移动到3针上。转移方程如下:

例题4-2:斐波那契数列
【问题描述】已知斐波那契数列公式如下,求斐波那契数列第n项的值。
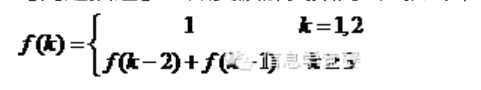
【分析】斐波那契数列是一个经典的递推问题。建立一个长度为n的数组,从小到大枚举递推即可。当然,此问题也可以用递归来解,但必须用记忆化搜索。
当n值过大时,(例如n≤1010),直接递推求解无法完成,在“数学方法”章节会具体讲述。
例题4-3:过河卒(NOIP2002初中组)
【问题描述】如图,A点有一个过河卒,需要走到目标B点。卒行走规则:可以向下、或者向右。同时在棋盘上的任一点有一个对方的马(如上图的C点),该马所在的点和所有跳跃一步可达的点称为对方马的控制点。例如上图C点上的马可以控制9个点(图中的P1, P2, … , P8和C)。卒不能通过对方马的控制点。
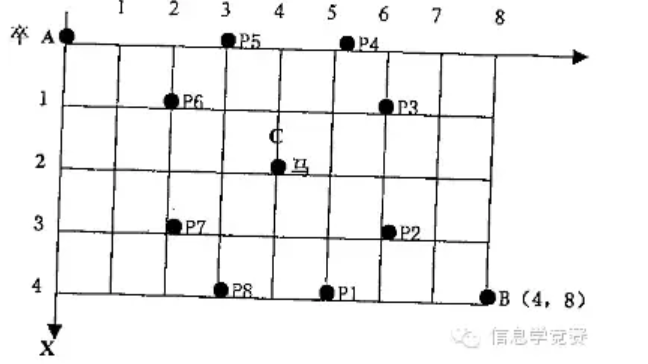
棋盘用坐标表示,A点(0,0)、B点(n,m) (n≤20,m≤20),马的位置坐标是C,现在要求你计算出卒从A点能够到达B点的路径的条数。
【分析】此题是一道非常老的题目,在很多书上也有类似的题目。此题盲目用搜索或者递归会超时。对本题稍加分析,卒的行走规律为可以向下或者向右走,当一个点被走过后,它不会再被走到。因此,可以递推进行,创建与棋盘同大小的数组,保存该点的可行方案数。我们用f(i,j)保存(i,j)点的可行方案数,g(i,j)保存(i,j)点是否被马控制,如果被控制,值为1,不被控制,值为0。递推公式如下:
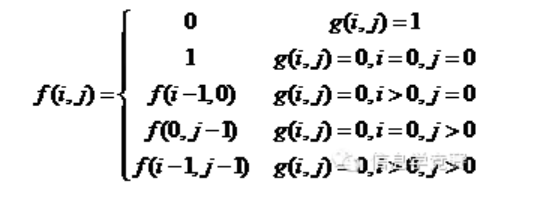
NOIP信息学视频地址
视频地址
链接:https://pan.baidu.com/s/1tHo1DFMaDuMZAemNH60dmw
提取码:7jgr


