NOIP--枚举
所谓枚举,就是将所有的可能一一遍历出来,在遍历中逐个检查答案的正确性,从而确定最终结果。
1. 知识点梳理:
Ø 一般枚举方法
一般枚举方法将所有可能情况都列举出来,理论上几乎可以解决所有问题。但是枚举算法的复杂度很高,需考虑时限问题。
Ø 枚举算法的优化
由于枚举法产生了大量的无用解,所以规模稍大的时候要进行优化。其中一类优化被称作“二分枚举”,其思路跟分治法(在后面的章节会讲)类似。在进行二分枚举时,其问题必须满足单调性。举个例子,给定单调函数f(x),计算f(x)与x轴的交点(精确到3位小数)。那么,对于区间[L,R],只需枚举中点,即可确定其子区间,最后当区间足够小时,即可确定解。设g(L,R)为f函数在区间[L,R]中与x轴的交点的横坐标值。
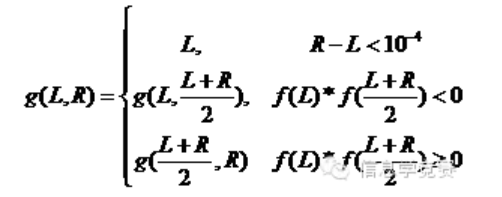
此类二分枚举实用性很强。有些问题直接求解比较复杂,或者难以想到时,可尝试二分枚举答案。这些问题通常具有性质:其判定型问题(给定一个解,看是否可行)比较容易求解。
1. 重难点分析:
u 枚举算法的时间开销一般较大,需要在算法设计时注意。
u 枚举不是万能的,不要盲目使用枚举法。
u 采用二分枚举时,需要保证所枚举的数据具有有序性。
u 在其他算法不满足时,可用枚举法获取部分分数。
2. 例题解析:
例题3-1:火柴棒等式(NOIP 2008)
【问题简述】给你n (n≤24) 根火柴棍,你可以拼出多少个形如 “A+B=C” 的等式?等式中的A、B、C是用火柴棍拼出的整数(若该数非零,则最高位不能是0),数字的形状和电子表上的一样。
注意:
1. 加号与等号各自需要两根火柴棍。
2. 如果A≠B,则A+B=C与B+A=C仍为不同的等式(A,B,C≥0)。
3. n根火柴棍必须全部用上。
【分析】本题就是一个经典的枚举题。由于题目中火柴数n≤24,A、B、C最大为3位数。首先先初始化0~9需要多少根火柴,再初始化0~999需要多少根火柴(当然,其中有一些是不可行的),接下来,枚举A和B,计算C,判断可行性。最差情况下为106次枚举。
例题3-2:关押罪犯(NOIP2010)
【问题描述】S 城现有两座监狱,一共关押着N (N≤20000) 名罪犯,编号分别为1~N。他们之间的关系自然也极不和谐。很多罪犯之间甚至积怨已久,如果客观条件具备则随时可能爆发冲突。我们用“怨气值”(一个正整数值)来表示某两名罪犯之间的仇恨程度,怨气值越大,则这两名罪犯之间的积怨越多。如果两名怨气值为c 的罪犯被关押在同一监狱,他们俩之间会发生摩擦,并造成影响力为c 的冲突事件。冲突的数目为M (M≤100000)。
每年年末,警察局会将本年内监狱中的所有冲突事件按影响力从大到小排成一个列表,然后上报到S 城Z 市长那里。公务繁忙的Z 市长只会去看列表中的第一个事件的影响力,如果影响很坏,他就会考虑撤换警察局长。
在详细考察了N 名罪犯间的矛盾关系后,警察局长觉得压力巨大。他准备将罪犯们在两座监狱内重新分配,以求产生的冲突事件影响力都较小,从而保住自己的乌纱帽。假设只要处于同一监狱内的某两个罪犯间有仇恨,那么他们一定会在每年的某个时候发生摩擦。那么,应如何分配罪犯,才能使Z 市长看到的那个冲突事件的影响力最小?这个最小值是多少?
【分析】此题最优解法是用并查集,复杂度为O(M log M)。在此我们只讲次优的二分枚举解法。
假如所有的罪犯之间的冲突只有0和1,那么题目就会变得非常简单。冲突为1的罪犯之间连一条边,直接染色即可。按照这个思路,可二分枚举冲突事件的影响力,对于小于当前枚举的影响力的冲突,不连边;对于大于当前枚举的影响力的冲突,连边。然后进行染色。时间复杂度为O(N log max(c))。在二分枚举的过程中,也可先对冲突进行排序,再二分枚举。时间复杂度变为O(N log M + M log M)。
二分枚举在NOIP中也十分常见。像2010年的“关押罪犯”和“QC”,2011年的“借教室”和“疫情控制”均可用二分枚举答案求解。
NOIP信息学视频地址
视频地址
链接:https://pan.baidu.com/s/1tHo1DFMaDuMZAemNH60dmw
提取码:7jgr


