NOIP--图论
图论当中最主要的组成部分
图。无图不成论,所以什么是图呢?我们一般用(Graph)来表示一张图,称为图。一张图可以表示为一个二元组,其中是点集,是边集,且(对于任意属于),为一个二元组且有。这就是图的定义。
其实我知道你们看不懂上面在说啥,上面只是一种形式化的定义。为了理解什么是图,我们换一种说法。考虑我们现在希望知道一些人之间的互相认识的关系。比如我们有个人,我们分别把他们叫做A、B、C。现在我们知道A和B互相认识,B和C互相认识,那么我们把每个人看做一个点,每对认识关系看做一条边,那么我们就可以画出这样一张图:
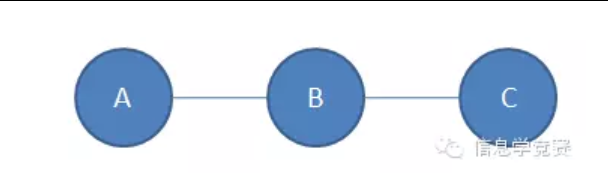
这张图中的每一个圆圈代表一个点对应一个人,每一条线代表一条边对应一对认识关系。所以我们可以从这张图里面读出以下信息:1、 有三个人A、B、C。(因为有三个点)2、 A和B认识,B和C认识。(因为A和B之间、B和C之间有边)3、 A和C不认识。(因为A和C之间没有边)这就是最简单的一张图。 通过上面这个简单的例子,大家对图论应该都有了一个简要的了解了
图论中的常见概念
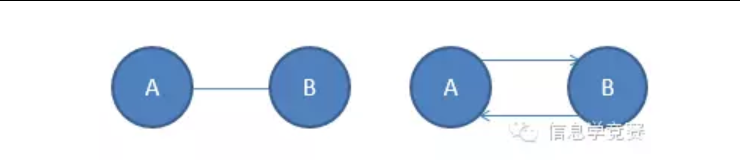
1、 有向图和无向图 什么叫有向图?什么又叫无向图?我们要知道取这样的一个名字是有意义的,所以我们就直接从字面上来理解这两样东西。所谓有向图,就是有方向的图;所谓无向图,就是没有方向的图。那么什么叫有方向,什么叫没有方向呢?我们来看下面的图:

这个是什么意思呢?看左边的图,我们可以理解为A和B都互相认识,或者说从A可以走到B,从B也可以走到A。右边的图是什么意思呢?我们可以理解为A认识B但B不认识A,就像你认识熊本熊但是熊本熊并不认识你,也就是说我们只能从A走到B而不能从B走到A。如果一张图里面的边有些没有方向有些有方向呢?这种时候我们还是把这样的图叫做有向图。 另外一点,所有的无向图都是可以表示为有向图的,方法如下图,这也是我们之后用来存储图的最常用的方法之一:(左右两张图是等价的)
2、 路径和环 我们首先来了解一下什么是路径。
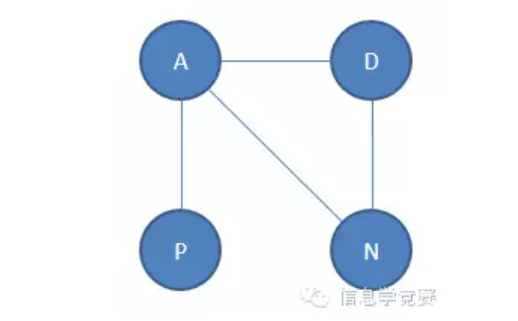
我们来考虑一下这张图,我们可以从P出发走到A然后走到N,再继续走到D然后又走到A。我们所经过的这个点的序列(P,A,N,D,A)就叫做一条路径。同理我们可以举出(P,A,D)这样的路径。注意到这两条路径(P,A,N,D,A)和(P,A,D)有一个重要的区别是,路径(P,A,D)并没有经过重复的点而路径(P,A,N,D,A)则经过了重复的点。我们把没有经过重复的点的路径就叫做简单路径。
环的定义是在路径的定义的基础上做了一定的拓展:首尾相接的路径我们就把它叫做一个环,比如(A,N,D,A)。同样我们也有简单环,也就是除开首尾以外,剩下的部分不会经过重复的点的环就叫做简单环。除此之外,还有一种最特殊的环,叫做自环。什么是自环呢,看一张图你就明白了:
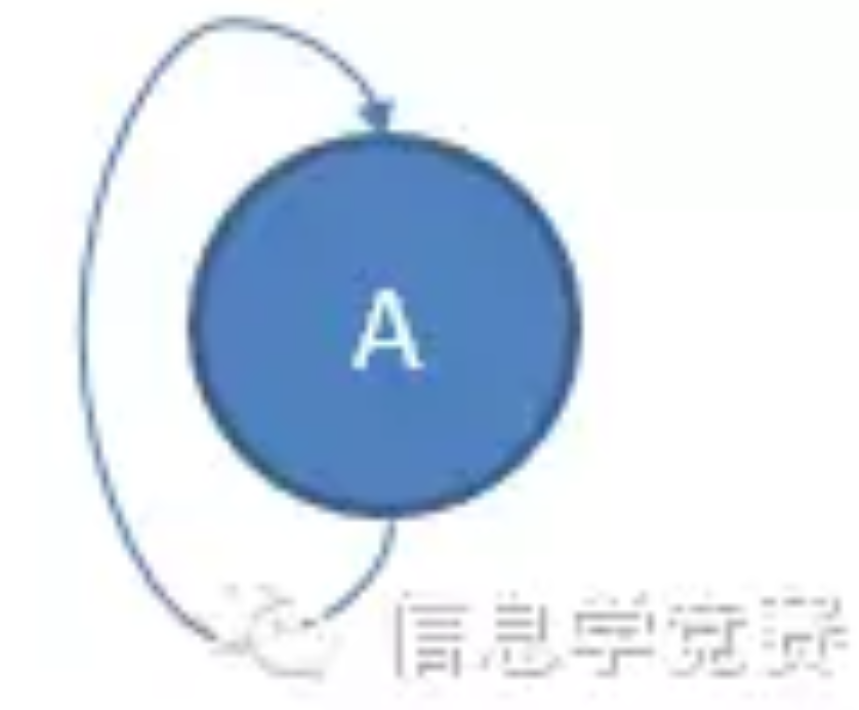
3、 子图。
我们把一张大图的点选一些出来,再选一些连在这些点之间的边出来,这样的小图就叫做子图。例如,下图中右边的图是左边的图的子图:
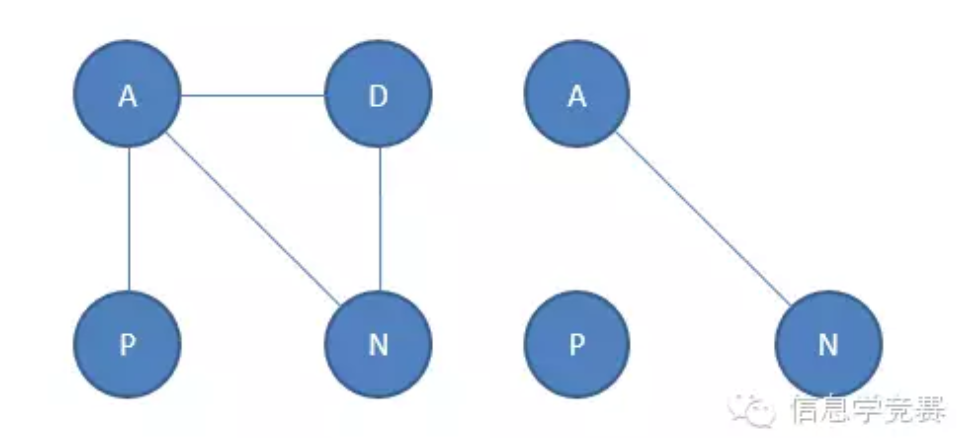
4、 连通图 首先是连通,什么是连通?如果存在一条从一个点到另外一个点的路径,那么这两个点就是连通的。(对于有向图也是一样的)那么什么叫做连通图呢?如果所有点都互相连通的话,这样一张图就叫做连通图。还是拿上面的图来举例,上面的图中左边的图是连通图,而右边的则不是。
5、 树和森林 一张连通图如果不存在环的话我们就叫做一棵树,如果一张图不存在环的话我们就把这张图叫做森林。接下来又是选择题的时间了,下列图中哪些是图论中的树,哪些是图论中的森林呢?

这上面当中是树的有D、E,而森林则是A、D、E(树是一种特殊的森林)
NOIP信息学视频地址
视频地址
链接:https://pan.baidu.com/s/1tHo1DFMaDuMZAemNH60dmw
提取码:7jgr


