NOIP-数据结构-二叉树

       这次我们来看看如何使用多叉树来处理数据。现在我们有一些集合我们要执行每次合并两个集合的操作，或者查询两个元素是否在同一个集合的操作我们就能够使用这种数据结构——并查集。一开始我们将每个集合中的元素都抽象成树中的点，并在每个集合中选出一个元素当做代表元，让这个集合中其他所有的点都以代表元这个点作为父节点。然后我们先看如何进行集合的合并操作，我们要合并两个集合就首先要找到这两个集合的代表元然后指定一个作为新的集合的代表元，然后让另一个代表元为他的子节点，其他的节点不变。那么我们如何通过任意的一个元素找到这个集合的代表元呢？这个很简单只要一直沿着他的父节点向上一直到根节点，那么根节点就是这个集合的代表元了。这样我们就很容易的知道如何判断两个元素是否在同一个集合，只要判断这两个元素所在的集合的代表元是否相等就可以了。

这样定义的并查集是十分简单的，然而正是因为这样的结构过于简单，我们还需要对这个结构进行一些优化，我们想一想如果一个集合被合并了很多次而且每次这个集合的代表元都没有成为大集合的代表元，那么查询这个集合中的元素所在集合的代表元将会花费很长的时间，而且我们在查询中很多时间都是重复劳动，所以是不是当我们查询完一个元素的所在集合的代表元之后直接将这个元素连到代表元的下方（即成为代表元的子节点），那么下次查询的时候是不是就会快很多了呢。虽然这样我们优化了查询这个点的时间，可是我们考虑一下在我们刚开始查询这个点的时候，中间路过的节点的所有的节点所在集合的代表元也可以求得，所以我么同样也可以将路上所有的节点都连到代表元的下方。我们将这种优化的方式称为路径压缩。        同样的问题我们可以还可以这样的操作，每次合并的时候我们比较一下那个集合比较大，每次选择大的集合的代表元作为整个集合的代表元。对于集合大小的比较只要我们开一个数组记录下每个集合的大小，合并时及时更新，比较时直接比较就好了。这样的优化方式我们称之为按秩合并。        同时使用这样的两种方式我们可以认为并查集的一次操作的代价是O(α(n)),其中α(n)是阿克曼函数的反函数，具体什么是阿克曼函数大家可以在网上搜索一下，我这里就不介绍了。说了这么多大家一定会觉得这样的一个数据结构很难实现，下面我给一个比较好的实现方式，首先对于这样的一个数据结构我们只关心他的父节点是谁，所以我们只记录父节点并且定义代表元的父节点是他自己。于是找代表元的代码如下：（我们用f[i]记录i的父节点）

 

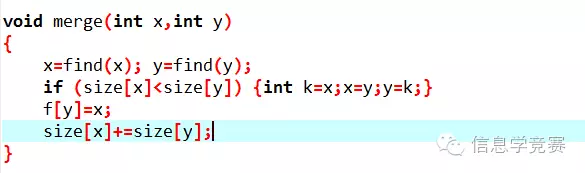
 这是合并两个集合的代码：

 

 

 

NOIP信息学视频地址

视频地址

链接：https://pan.baidu.com/s/1tHo1DFMaDuMZAemNH60dmw 
提取码：7jgr