NOIP-数据结构-堆
如果我们一开始就有n个数据,如何将他们快速的建立一个堆,当然我们可以将堆从空一直执行插入操作,这样的算法的复杂度为O(log1+log2+…+logn)经过数学计算这个复杂度是O(nlogn)的。接下来我们介绍一种快速的建立堆的方法,按照数据的顺序直接将他们放入树中,接下来我们从第n/2个数据开始判断他是否比他的左右儿子小,如果是则不进行任何操作,如果不是,则将左右儿子中小的那个节点和他互换,然后继续这样的判断。然后我们判断第n/2-1个数据是否满足,直到判断到第1个数据。我们来看一个简单的例子:假如我们的原始数据是2,8,7,5,3,9,4
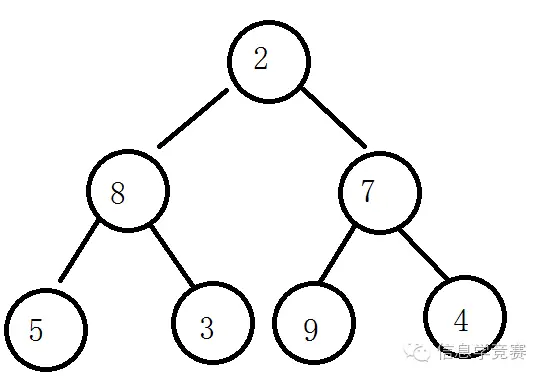
这样的树显然不是一个堆,我们先判断n/2个数据也就是7是否满足要求
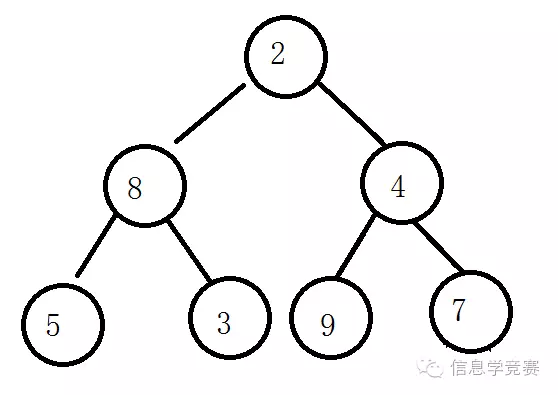
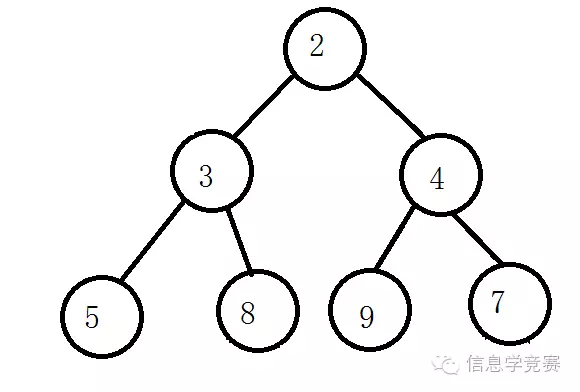
然后判断8和2最终的树就是
我们知道了这样的算法我们肯定还有疑问为什么这样的算法会比我们一个一个插入的算法要快,我们来算一算,假如我们的树有k层,在第j层的节点我们已经知道最多是2j个节点,这些节点最多只会做k-j次移动,于是我们的总移动次数就是O(k*1+(k-1)*2+(k-2)*4+…(k-(k-1))*2k-1)=O(2k)也就是O(n).所以这个建立堆的方法的复杂度是O(n),比我们单独插入的复杂度要优秀的多 。
接下来我们来看一个堆的具体应用。
合并果子:我们有n堆果子,每次可以合并任意两堆合并的代价是两堆果子的数量和,问最后将这些果子合并成一堆时所需要的最小的代价。 这样的一个问题是有着贪心的做法的,每次选择果子数最少的两堆果子将其合并就可以得到最优的解答了。于是我们可以利用我们所学的堆的知识,现将所有的果子数建成一个堆每次从堆顶拿出一个数并将它删除,在拿出一个数并将它删除将这两数的和加入答案,并把他们的和加入堆中。由于将n堆果子合并成一堆果子一共需要合并n-1次,并且每次操作的复杂度是logn的所以完成这样的一个问题的复杂度为O(nlogn)
最后大家值得注意的是我们在介绍堆的时候,一直在说每个节点的值比左右儿子节点的值要小的这样的一个关系,其实在实现堆的时候,我们所说的小不一定是真正意义上的小的关系,这样的小的关系是我们自己定义的比如用大于号来定义这样的一个小的关系,或者用自己定义的小的关系都能够实现一个堆,只是在判断的时候要注意小的关系就可以了。
NOIP信息学视频地址
视频地址
链接:https://pan.baidu.com/s/1tHo1DFMaDuMZAemNH60dmw
提取码:7jgr


