NOIP-数据结构3

如果现在在我们面前有一堆的数据然后我们想支持查询这些数据中最小的那个数据，新增加一个数据，删除最小的数据，这时我们将可以使用堆这个数据结构。

   首先我们先来看看堆的样子。堆是一个完全二叉树，对于每一个二叉树上的节点满足这个节点上的数据小于他的儿子节点上的数据（如果这个节点有儿子），这样构成的数据结构叫做堆。比如我们在每个节点上标出他们的数据这样的一个二叉树就是一个堆了。

 

 

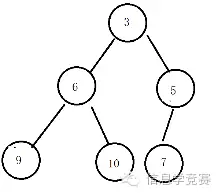
通过这个定义我们可以很明显的发现，整个树的根就是数据中最小的那个元素，于是我们就能够很轻松的完成取出最小的那个元素的操作了。

  然后我们看看这样的一个结构如何实现插入某一个数据，首先我们可以在最靠上（同样深度时靠左）的一个儿子结点没有满的节点上新建一个儿子结点，然后将这个数据放到这个新的节点上面，然后比较这个节点的数据是否比他的父亲节点的数据小，如果不是那么插入就完成了，否则为了满足堆的性质我们就要将这个节点和他的父亲节点互换位置，知道他比他的父亲节点小，或者他就是根节点了。我们下面来看看在上述的堆中如何插入一个数值为4的数据。

 

 

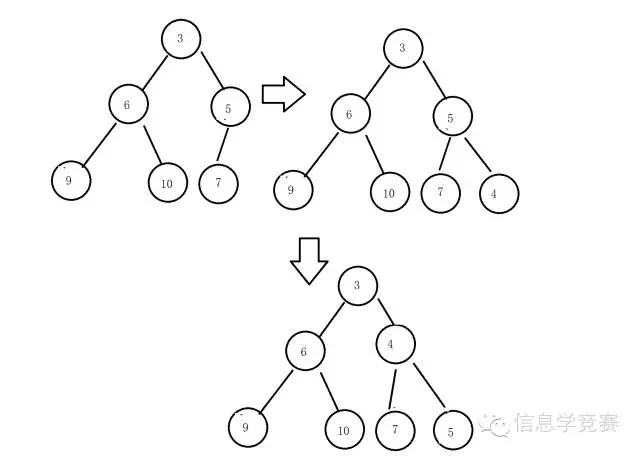
我们接下来分析一下这个操作的复杂度，首先如果现在一个堆中的数据有n个那么这个树的层数为logn-1（logn=x 当且仅当2^x=n）向上取整。应为我们的第一层节点最多一个，第二层节点最多两个，第i层节点最多2ⁱ个，所以我们可以发现i层的树的总结点最多可以达到2ⁱ⁺¹-1个我们的堆又是一个满二叉树所以我们的层数最多就是logn-1，每次插入操作我们最多只会把一个节点从叶子挪到根所以插入的复杂度可以认为是O（logn）的

然后是删除操作我们已经知道了最小值在根上了，如何才能够快速的将这个节点删除呢，我们采取这样的办法，首先将根与最下（同样层数最右）的节点互换，然后将换到叶子的这个节点直接删除。在考虑换到根的节点，看看他是否满足堆的性质也就是他是不是比他的左右儿子的值都小，如果是那么我们的删除操作就结束了，否则我们为了保持堆的性质就要将左右儿子中小的那一个节点和这个节点互换，直到他没有儿子了或者他已经满足堆的性质了。我们再来通过一个例子来看看堆的删除操作。

 

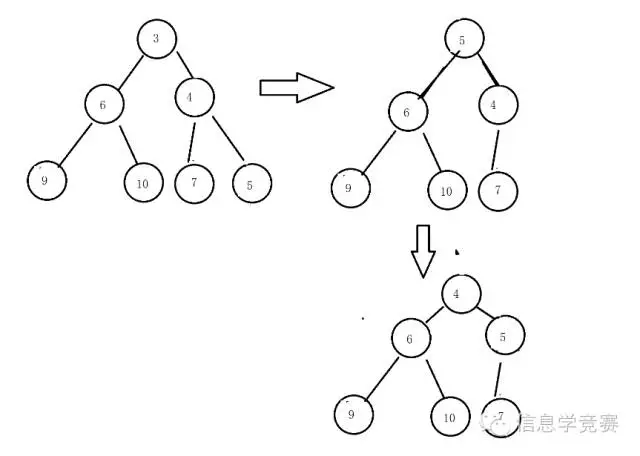
 和分析堆的插入的例子一样在堆中删除一个节点的复杂度也是O（logn）的，因为对于一个节点他也最多只会从根一路被放到叶子，最多只会进过logn层。

 

NOIP信息学视频地址

视频地址

链接：https://pan.baidu.com/s/1tHo1DFMaDuMZAemNH60dmw 
提取码：7jgr