有限元二阶拉格朗日插值函数理论

上一个博客学习了一阶拉格朗日插值，这次准备学习二阶拉格朗日插值，但是因为找不到合适的画网格软件给出二阶拉格朗日插值下的三角形单元坐标，并且二阶与一阶之间有很大相似性，所以此处只讲理论，不再编程。

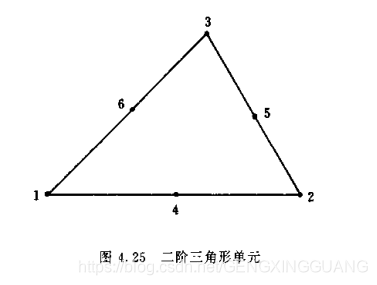
1. 对于插值函数存在一些定理，令阶数用符号n表示，则单个三角形单元，节点分布的位置和满足顺序为:三个顶点各一个节点+每条边为(n-1)个顶点+其余在单元内部。至于总共有多少个顶点，公式为m=0.5*(n+1)*(n+2)
2. 由上面可知，二阶插值有6个顶点，分布如下图
3. 
4. 二阶插值也可以借助面积坐标进行简化：u=u1*lamda1+u2*lamda2+u3*lamda3+u4*lamda4+u5*lamda5+u6*lamda6
   1. 
   2. 每个lamda的值即为上式的phi,而式子中的epsilon1, epsilon2,epsilon3即为面积坐标表达式
5. 有个插值函数，则按照上个博客的方法求出每个单元刚度矩阵及载荷即可。
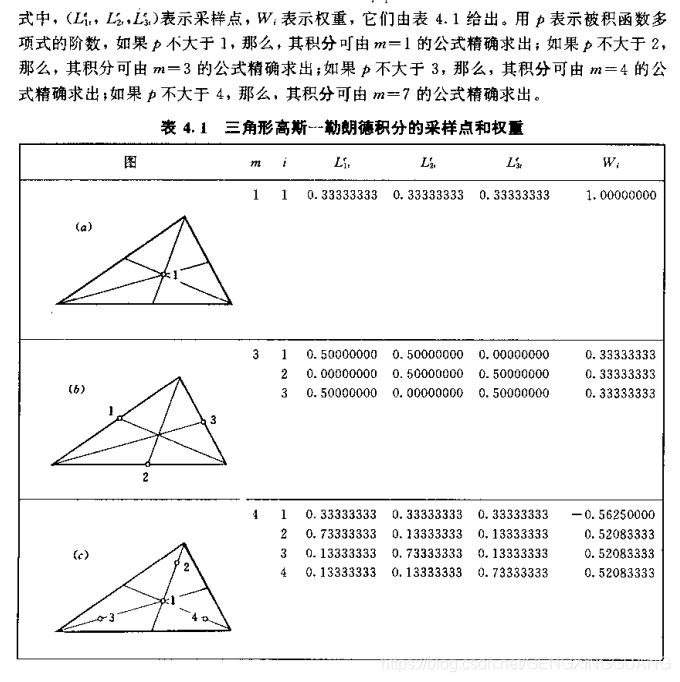
6. 二阶求积分比一阶复杂，因此有两个辅助方法可以帮助简单求解积分
   1. 面积坐标下的积分表达式
      1. 
      2. 
   2. 三角形的高斯-勒朗德积分
      1. 
      2. 
   3. 最后就是求解