Link Cut Tree学习笔记
从这里开始
动态树问题和Link Cut Tree
动态树问题是一类要求维护一个有根树森林,支持对树的分割, 合并等操作的问题。
Link Cut Tree(林可砍树?简称LCT)是解决这一类问题的一种数据结构。
一些无聊的定义
Link Cut Tree维护的是动态森林中每棵树的任意链剖分。
Preferred Child,每个点偏好的子节点,对于每个点,要么它没有,要么它只有一个。
Preferred Edge,连接每个点和它偏好的子节点的边,以下简称为实边。
相对地,对于非实边的边,以下简称为虚边。
Preferred Path,由Preferred Edge 连接成的不可再延伸的路径。以下简称为实链。特殊地,如果与一个点相连的所有边都是虚边,那么这一个点独自构成一条实链。
显然,所有实链覆盖所有的点。
对于每条实链,LCT用一颗Splay对节点按深度为关键字进行维护。
//接下来会默认读者能熟练地敲打Splay的板子
为了方便直接用Splay森林来维护。对于每棵Splay,它还需要维护它的维护的实链的顶端(深度最小的点)的父节点,这个记在根结点上。
access操作
access操作是将某个节点$x$到根的路径变为实链。
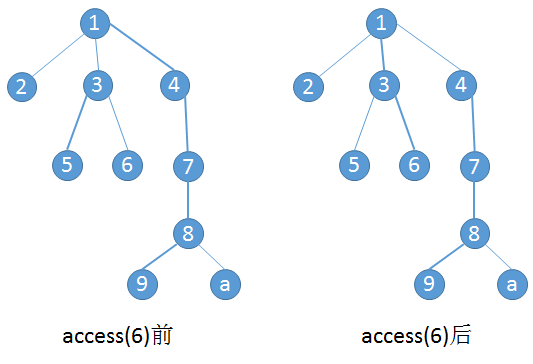
由图中可以看出,access操作可以看成以下几个操作的反复进行:
- 断掉当前实链中当前点和比它深的点之间的实边
- 合并当前实链和上一条实链
- 访问实链顶端的父节点
当当前点为空的时候结束,不存在上一条实链的时候它为空。
显然这样操作恰好将指定点到根的路径变为实链了。
1 void access(SplayNode *p) { 2 SplayNode* q = NULL; 3 while (p) { 4 splay(p); 5 q = p, p = p->fa; 6 } 7 }
换根操作
将一棵树的根变为指定点。
考虑换根操作的影响:
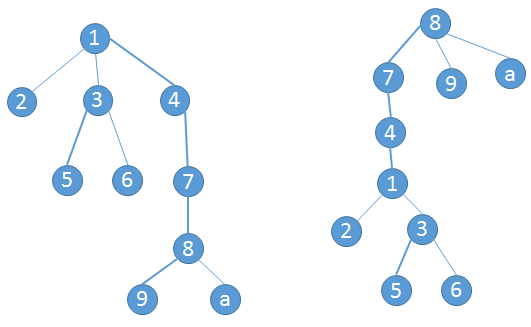
只是旧根到新根的路径被翻转了。那就先对新根执行access操作,然后打反转标记就好了。
1 void mkroot(SplayNode* node) { 2 access(node); 3 splay(node); 4 node->rev ^= 1; 5 }
link和cut操作
link操作是连接两个不连通的点,cut操作是删除一条原有的边。
考虑link操作,将其中一个作为根然后向另一个点连接一条虚边即可。
考虑cut操作,将其中一个作为根,然后对另一个点做access操作,这样恰好根所在的Splay中的后继是另一个点,Splay树上断掉这条边即可。
1 void link(int u, int v) { 2 SplayNode* p = pool + u, *q = pool + v; 3 if(isConnected(p, q)) return ; 4 mkroot(q); 5 q->fa = p, splay(q); 6 } 7 8 void cut(int u, int v) { 9 SplayNode* p = pool + u, *q = pool + v; 10 mkroot(p); 11 access(q); 12 splay(q); 13 q->ch[0] = p->fa = NULL; 14 }
例1 Cave 洞穴勘测
题目大意
给定一个动态森林,要求支持加边、删边和询问两点之间的连通性。
判断两点之间是否连通,等价于它们所在的树的根相同。
所以考虑如何找一个点所在树的根。
首先access这个点,然后把它伸展到根,然后暴力跳左子树就好了。
Code

1 /** 2 * bzoj 3 * Problem#2049 4 * Accepted 5 * Time: 1976ms 6 * Memory: 1500k 7 */ 8 #include <bits/stdc++.h> 9 using namespace std; 10 typedef bool boolean; 11 12 typedef class SplayNode { 13 public: 14 boolean rev; 15 SplayNode *ch[2]; 16 SplayNode *fa; 17 18 SplayNode():rev(0), ch({NULL, NULL}), fa(NULL) { } 19 20 boolean isRoot() { 21 if(fa == NULL) return true; 22 return fa->ch[0] != this && fa->ch[1] != this; 23 } 24 25 void pushDown() { 26 swap(ch[0], ch[1]); 27 if(ch[0]) ch[0]->rev ^= 1; 28 if(ch[1]) ch[1]->rev ^= 1; 29 rev = 0; 30 } 31 }SplayNode; 32 33 typedef class LinkCutTree { 34 public: 35 SplayNode *pool; 36 37 LinkCutTree():pool(NULL) { } 38 LinkCutTree(int n) { 39 pool = new SplayNode[(n + 1)]; 40 } 41 42 void rotate(SplayNode* node) { 43 SplayNode* fa = node->fa; 44 boolean aFlag = fa->isRoot(); 45 int d = fa->ch[1] == node; 46 fa->ch[d] = node->ch[d ^ 1]; 47 node->fa = fa->fa; 48 fa->fa = node; 49 node->ch[d ^ 1] = fa; 50 if(fa->ch[d]) fa->ch[d]->fa = fa; 51 if(!aFlag) node->fa->ch[node->fa->ch[1] == fa] = node; 52 } 53 54 SplayNode* s[10005]; 55 void splay(SplayNode* node) { 56 int top = 0; 57 s[++ top] = node; 58 for (SplayNode* p = node; !p -> isRoot(); p = p->fa) s[++ top] = p -> fa; 59 for (int i = top; i; -- i) if (s[i] -> rev) s[i] -> pushDown(); 60 while(!node->isRoot()) { 61 SplayNode *fa = node->fa, *ffa = fa->fa; 62 if(fa->isRoot()) { 63 rotate(node); 64 break; 65 } 66 int d1 = (fa->ch[1] == node), d2 = ffa->ch[1] == fa; 67 if(d1 == d2) 68 rotate(fa); 69 else 70 rotate(node); 71 rotate(node); 72 } 73 } 74 75 SplayNode* findSplayRoot(SplayNode* node) { 76 access(node); 77 // while(node->fa) node = node->fa; 78 splay(node); 79 while(node->ch[0]) node = node->ch[0]; 80 return node; 81 } 82 83 void access(SplayNode* node) { 84 SplayNode* p = NULL; 85 do { 86 splay(node); 87 node->ch[1] = p; 88 p = node; 89 node = node->fa; 90 } while (node); 91 } 92 93 boolean isConnected(SplayNode* p, SplayNode* q) { 94 return findSplayRoot(p) == findSplayRoot(q); 95 } 96 97 void mkroot(SplayNode* node) { 98 access(node); 99 splay(node); 100 node->rev ^= 1; 101 } 102 103 void link(int u, int v) { 104 SplayNode* p = pool + u, *q = pool + v; 105 if(isConnected(p, q)) return ; 106 mkroot(q); 107 q->fa = p, splay(q); 108 } 109 110 void cut(int u, int v) { 111 SplayNode* p = pool + u, *q = pool + v; 112 mkroot(p); 113 access(q); 114 splay(q); 115 q->ch[0] = p->fa = NULL; 116 } 117 118 boolean isConnected(int u, int v) { 119 return isConnected(pool + u, pool + v); 120 } 121 }LinkCutTree; 122 123 int n, m; 124 LinkCutTree lct; 125 char buf[15]; 126 int u, v; 127 inline void solve() { 128 scanf("%d%d", &n, &m); 129 lct = LinkCutTree(n); 130 while(m--) { 131 scanf("%s%d%d", buf, &u, &v); 132 switch(buf[0]) { 133 case 'C': 134 lct.link(u, v); 135 break; 136 case 'D': 137 lct.cut(u, v); 138 break; 139 case 'Q': 140 puts((lct.isConnected(u, v)) ? ("Yes") : ("No")); 141 break; 142 } 143 } 144 } 145 146 int main() { 147 solve(); 148 return 0; 149 }
时间复杂度证明
如果学习一个数据结构能证明它的时间复杂度那就再好不过了。
对于LCT的操作,基本上是access,然后加上某些$O(1)$的操作或者均摊$O(\log n)$的Splay操作。所以只需要证明access的时间复杂度是$O(\log n)$即可。
在开始证明前,你需要知道Splay的时间复杂度和一些常识性的东西。
定理1 对于操作splay(x),设操作前$x$的子树大小为$siz[x]$,操作后的子树大小为$siz'[x]$,splay(x)的均摊时间复杂度小于等于$3(\log siz'[x] - \log siz[x]) + 1$
证明略去(其实是我不会)
下面一个是关于轻重链剖分的常识,证明可以看这篇随笔。
定理2 一条根节点到叶节点的路径上,轻边的条数不超过$\log_{2}n$条
然后还有一个需要证明的事情。
定理3 Preferred Child的改变次数均摊为$O(log_{2}n)$次
证明 因为每次Preferred Child的改变时会导致实边发生改变。所以考察实边改变的次数即可。
这一部分可以分为两种情况:
- 一条轻虚边被改为轻实边。
- 一条重虚边被改为重实边。
因为轻边总数不超过$\log_{2}n$条,所以第一部分的改变次数不超过$\log_{2}n$次。
考虑重虚边被改为重实边的情况。
考虑每一条重边,它从实变为虚,虚变为实的过程是交替进行的。所以它被改为实边的次数不会超过它从实边被改为虚边的次数加1。
当一条重实边被改为重虚边会导致一条轻虚边变为轻实边,同时我们证明了轻虚边变为轻实边的均摊次数不超过$O(log_{2}n)$,所以一条重虚边被改为重实边的次数也不超过$O(log_{2}n)$。
因此定理得证。
定理4 access的均摊时间复杂度为$O(log_{2}n)$
证明 设每次设为当前点的点依次为$v_{0}, v_{1}, v_{2},\cdots,v_{k}$。
那么有:
$\widehat{cost}\leqslant 3\left (\sum_{i = 1}^{k}\log siz[v_{i}] - \log siz[v_{i - 1}] + 1 \right ) + \log siz[v_{0}]$
所以化简后再根据定理3,可得:
$\widehat{cost}\leqslant 6\log{n}$
Link Cut Tree维护链上信息
对于有关边权的链上信息考虑为每条边建一个虚点。然后和它两端连边。
查询链上信息可以通过把一个点变为根,access另一个点后的splay中的信息就是这条链上的信息。
但是有些装逼爱好者觉得这样不能满足他们的欲望,想出了一种不用建虚点的方法。很开心的是细节超多,看到neither_nor的某道题写了200+行,想想得到结论——装逼是要有代价的。
这个方法的讲解:neither_nor神犇的博客
例2 魔法森林
题目大意
一张图有$n$个点,$m$条边,第$i$条边有两个边权$a_{i}$和$b_{i}$。定义从1号点走到$n$号点的代价是经过边的所有$a$边权的最大值加上所有$b$边权的最大值。
问从1号点走到$n$号点的最小代价。
高维问题常见思路是降维,因此考虑按照$a$边权排序,然后枚举。
假设图开始是空的,然后依次加入每一条边。
- 如果边的两端未连通,直接加就好了。
- 如果边的两端连通,那么会形成环。根据人生的经验和图论的哲理,可以知道,环是这两点在树上的简单路径再加上这一条边。那么找到换上$b$边权最大的一条边比较它和当前边的$b$边权。如果当前边的$b$边权更小,那么就把树上的那条边cut掉,然后把这条新边加上。
如果在某个时候1和$n$连通,就查询一下它们之间的简单路径中$a$边权和$b$边权的最大值就好了。
由于这里的“删边”不会改变连通性(因为马上你会加一条边),所以可以直接用并查集维护连通性。
Code

1 /** 2 * uoj 3 * Problem#3 4 * Accepted 5 * Time: 2287ms 6 * Memory: 11208k 7 */ 8 #include <bits/stdc++.h> 9 using namespace std; 10 typedef bool boolean; 11 12 typedef class SplayNode { 13 public: 14 boolean rev; 15 int ea, eb, idx; 16 int ma, mb, ib; 17 SplayNode *ch[2]; 18 SplayNode *fa; 19 20 SplayNode():rev(false), ea(0), eb(0), idx(0), ma(0), mb(0), ib(0), ch({NULL, NULL}), fa(NULL) { } 21 22 void pushUp() { 23 ma = ea, mb = eb, ib = idx; 24 for (int i = 0; i < 2; i++) 25 if (ch[i]) { 26 (ch[i]->ma > ma) ? (ma = ch[i]->ma) : (0); 27 (ch[i]->mb > mb) ? (mb = ch[i]->mb, ib = ch[i]->ib) : (0); 28 } 29 } 30 31 void pushDown() { 32 swap(ch[0], ch[1]); 33 if (ch[0]) ch[0]->rev ^= 1; 34 if (ch[1]) ch[1]->rev ^= 1; 35 rev = false; 36 } 37 38 boolean isroot() { 39 return !fa || (fa->ch[0] != this && fa->ch[1] != this); 40 } 41 42 int which() { 43 return (!isroot()) ? (fa->ch[1] == this) : (-1); 44 } 45 }SplayNode; 46 47 typedef class LinkCutTree { 48 public: 49 SplayNode* pool; 50 SplayNode** s; 51 int top, n; 52 53 LinkCutTree() { } 54 LinkCutTree(int n, int m):n(n) { 55 pool = new SplayNode[(n + m + 1)]; 56 s = new SplayNode*[(n + m + 1)]; 57 } 58 59 void rotate(SplayNode* p) { 60 int d = p->which(), df = p->fa->which(); 61 SplayNode* fa = p->fa, *ffa = fa->fa, *ls = p->ch[d ^ 1]; 62 fa->ch[d] = ls, (ls) ? (ls->fa = fa) : (0); 63 p->fa = ffa, (~df) ? (ffa->ch[df] = p) : (0); 64 p->ch[d ^ 1] = fa, fa->fa = p; 65 fa->pushUp(), p->pushUp(); 66 } 67 68 void splay(SplayNode* p) { 69 SplayNode *np = p; 70 for (top = 0; s[++top] = np, !np->isroot(); np = np->fa); 71 for ( ; top; top--) 72 if (s[top]->rev) 73 s[top]->pushDown(); 74 for ( ; !p->isroot(); rotate(p)) 75 if (!p->fa->isroot()) 76 rotate((p->which() == p->fa->which()) ? (p->fa) : (p)); 77 } 78 79 void access(SplayNode *p) { 80 SplayNode* q = NULL; 81 while (p) { 82 splay(p); 83 p->ch[1] = q; 84 p->pushUp(); 85 q = p, p = p->fa; 86 } 87 } 88 89 void mkroot(SplayNode *p) { 90 access(p); 91 splay(p); 92 p->rev ^= 1; 93 } 94 95 void link(SplayNode* p, SplayNode* q) { 96 mkroot(q); 97 q->fa = p; 98 } 99 100 void cut(SplayNode* p, SplayNode* q) { 101 mkroot(p); 102 access(q); 103 p->ch[1] = q->fa = NULL; 104 p->pushUp(); 105 } 106 107 SplayNode* query(int u, int v) { 108 SplayNode* p = pool + u, *q = pool + v; 109 mkroot(p), access(q); 110 splay(p); 111 return p; 112 } 113 114 void link(int u, int v, int a, int b, int idx) { 115 SplayNode* p = pool + u, *q = pool + v, *es = pool + n + idx; 116 es->ea = es->ma = a, es->eb = es->mb = b, es->ib = es->idx = idx; 117 link(p, es), link(es, q); 118 } 119 120 void cut(int u, int v, int idx) { 121 SplayNode *p = pool + u, *q = pool + v, *es = pool + n + idx; 122 cut(p, es), cut(es, q); 123 } 124 125 void debugOut(SplayNode* p) { 126 if (!p) return; 127 fprintf(stderr, "%d (fa: %d, ea: %d, eb: %d, ma: %d, mb: %d, idx: %d, ib: %d, flag: %d) {", p - pool, (!p->fa) ? (0) : (p->fa - pool), p->ea, p->eb, p->ma, p->mb, p->idx, p->ib, p->rev); 128 debugOut(p->ch[0]); 129 fprintf(stderr, ", "); 130 debugOut(p->ch[1]); 131 fprintf(stderr, "}"); 132 } 133 134 void debugOut() { 135 fprintf(stderr, "--------------------\n"); 136 for (int i = 1; i <= 7; i++) 137 if (pool[i].isroot()) 138 debugOut(pool + i), fprintf(stderr, "\n"); 139 } 140 }LinkCutTree; 141 142 typedef class Edge { 143 public: 144 int u, v, a, b; 145 146 boolean operator < (Edge b) const { 147 return a < b.a; 148 } 149 }Edge; 150 151 int n, m; 152 int res = 211985; 153 int* f; 154 Edge* es; 155 LinkCutTree lct; 156 157 int find ( int x ) { 158 while ( x != f [x] ) x = f [x] = f [f [x]] ; 159 return x ; 160 } 161 162 inline void init() { 163 scanf("%d%d", &n, &m); 164 f = new int[(n + 1)]; 165 es = new Edge[(m + 1)]; 166 lct = LinkCutTree(n, m); 167 for (int i = 1; i <= n; i++) 168 f [i] = i ; 169 for (int i = 1; i <= m; i++) 170 scanf("%d%d%d%d", &es[i].u, &es[i].v, &es[i].a, &es[i].b); 171 } 172 173 inline void solve() { 174 SplayNode* p; 175 sort(es + 1, es + m + 1); 176 for (int i = 1, u, v, a, b; i <= m; i++) { 177 u = es[i].u, v = es[i].v, a = es[i].a, b = es[i].b; 178 if (u == v) continue; 179 if (find(u) != find(v)) { 180 lct.link(u, v, a, b, i);//, cerr << u << " " << v << endl; 181 f [find ( u )] = find ( v ) ; 182 } 183 else { 184 // cerr << "R:" << u << " " << v << endl; 185 p = lct.query(u, v); 186 if (p->mb > b) { 187 lct.cut(es[p->ib].u, es[p->ib].v, p->ib); 188 lct.link(u, v, a, b, i); 189 } 190 } 191 if (find ( 1 ) == find (n)) { 192 p = lct.query(1, n); 193 res = min(res, p->ma + p->mb); 194 // cerr << "Q" << endl; 195 } 196 // lct.debugOut(); 197 } 198 printf("%d\n", (res == 211985) ? (-1) : (res)); 199 } 200 201 int main() { 202 srand(233); 203 init(); 204 solve(); 205 return 0; 206 }
Link Cut Tree维护子树信息
首先来说说一些无聊的定义。
众所周知,LCT维护的是一个动态森林的链剖分。
定义一个点的LCT子树是这个点在Splay上的子树。
所以LCT子树可能并不是原树中的子树,它可能包含这个点的祖先。
一个点的所有虚子树是在Splay中所有与它通过虚边相连的点的LCT子树。
一个点的所有实子树是在Splay中它的左右子树。
因此一个点的LCT子树等于它的所有虚子树加上它的所有实子树和它自己。
某个很有用的性质 将一个点access后,它的虚子树信息再加上它自己的信息就是它的在原树中的子树信息。
因为access这个点之后它就没有Preferred Child,它的所有子节点都和它通过虚边相连。它的子节点的LCT子树不包含后代,所以恰好是原树中的子树信息。
考虑什么时候虚子树信息会改变:
- 当access一个点后
- 当进行link和cut操作时
情况1很好处理,断开一条实边的时候加上它的LCT子树信息,添加一条实边的时候减去它的LCT子树信息。
看起来现在需要维护LCT子树信息,也就是说修改后还需要将信息上传。
但是access进行断边的时候能够保证当前点是Splay的根,所以通常不用上传任何信息(因为通常它的LCT子树信息不会改变)。
考虑link操作,我们会添加一条虚边,它会改变一个点的子树信息以及它的祖先的子树信息。
所以我们先access它,然后把它伸展到根,于是就巧妙地避开了更新祖先的子树信息。
继续考虑cut操作,我们会断掉1条边,可以用同样的方法进行处理。
注意事项
- Splay的形态发生改变时会改变LCT子树信息但是不会改变虚子树信息
- 发生虚实边的改变时才会导致虚子树信息发生改变
- 修改时要考虑信息上传的问题,如果难以上传可以考虑避开上传,或者直接进行链上修改。
例3 大融合
题目大意
维护一个动态森林,要求支持
- 添加一条边
- 询问经过一条边的所有简单路径数
假如是一个静态森林,那么如果处理询问操作?
这条边会把树分成两部分,对吧?答案是这两个部分的点数的乘积。
考虑如何在动态森林中维护子树大小,还是很显然的。
那么如何算答案?
把其中一个变成根,然后就可以计算两部分的点数了。
Code

1 /** 2 * bzoj 3 * Problem#4530 4 * Accepted 5 * Time: 1124ms 6 * Memory: 3488k 7 */ 8 #include <bits/stdc++.h> 9 #ifndef WIN32 10 #define Auto "%lld" 11 #else 12 #define Auto "%I64d" 13 #endif 14 using namespace std; 15 typedef bool boolean; 16 17 #define ll long long 18 19 typedef class SplayNode { 20 public: 21 boolean rev; 22 int ls, vs; 23 SplayNode* ch[2]; 24 SplayNode* fa; 25 26 SplayNode():rev(false), ls(1), vs(0), ch({NULL, NULL}), fa(NULL) { } 27 28 void pushUp() { 29 ls = 1 + vs; 30 if (ch[0]) ls += ch[0]->ls; 31 if (ch[1]) ls += ch[1]->ls; 32 } 33 34 void pushDown() { 35 swap(ch[0], ch[1]); 36 if (ch[0]) ch[0]->rev ^= 1; 37 if (ch[1]) ch[1]->rev ^= 1; 38 rev = false; 39 } 40 41 boolean isRoot() { 42 if (!fa) return true; 43 return fa->ch[0] != this && fa->ch[1] != this; 44 } 45 }SplayNode; 46 47 typedef class LinkCutTree { 48 public: 49 int top; 50 SplayNode* pool; 51 SplayNode** s; 52 53 LinkCutTree():pool(NULL), s(NULL) { } 54 LinkCutTree(int n):top(0) { 55 pool = new SplayNode[(n + 1)]; 56 s = new SplayNode*[(n + 1)]; 57 } 58 59 void rotate(SplayNode *p) { 60 int d = (p->fa->ch[1] == p), d1 = (p->fa->fa) ? (p->fa->fa->ch[1] == p->fa) : (-1); 61 SplayNode *fa = p->fa, *ffa = fa->fa, *ls = p->ch[d ^ 1]; 62 boolean sign = fa->isRoot(); 63 p->ch[d ^ 1] = fa, fa->fa = p; 64 fa->ch[d] = ls, (ls) ? (ls->fa = fa) : (0); 65 p->fa = ffa, (!sign && ~d1) ? (ffa->ch[d1] = p) : (0); 66 fa->pushUp(), p->pushUp(); 67 } 68 69 void splay(SplayNode* p) { 70 SplayNode *np = p, *fp = p->fa; 71 for (top = 0; s[++top] = np, !np->isRoot(); np = np->fa); 72 for (; top; top--) 73 if (s[top]->rev) 74 s[top]->pushDown(); 75 for (; !p->isRoot(); rotate(p), fp = p->fa) 76 if (!fp->isRoot()) 77 rotate(((fp->fa->ch[1] == fp) == (fp->ch[1] == p)) ? (fp) : (p)); 78 } 79 80 void access(SplayNode *p) { 81 SplayNode *q = NULL; 82 while (p) { 83 splay(p); 84 p->vs += ((p->ch[1]) ? (p->ch[1]->ls) : (0)); 85 p->vs -= ((q) ? (q->ls) : (0)); 86 p->ch[1] = q; 87 p->pushUp(); 88 q = p, p = p->fa; 89 } 90 } 91 92 void mkroot(SplayNode *p) { 93 access(p); 94 splay(p); 95 p->rev ^= 1; 96 } 97 98 void link(int u, int v) { 99 SplayNode *a = pool + u, *b = pool + v; 100 mkroot(b); 101 access(a); 102 splay(a); 103 b->fa = a; 104 a->vs += b->ls; 105 a->pushUp(); 106 } 107 108 SplayNode* findPre(SplayNode* p) { 109 splay(p); 110 p = p->ch[0]; 111 while (p) { 112 if (p->rev) p->pushDown(); 113 if (!p->ch[1]) break; 114 p = p->ch[1]; 115 } 116 return p; 117 } 118 119 ll query(int u, int v) { 120 SplayNode *p = pool + u, *q = pool + v; 121 mkroot(p); 122 access(q); 123 splay(p); 124 int s1 = q->vs + 1, s2 = p->ls; 125 return s1 * 1ll * (s2 - s1); 126 } 127 }LinkCutTree; 128 129 int n, m; 130 LinkCutTree lct; 131 132 inline void init() { 133 scanf("%d%d", &n, &m); 134 lct = LinkCutTree(n); 135 } 136 137 inline void solve() { 138 char s[5]; 139 int u, v; 140 while (m--) { 141 scanf("%s%d%d", s, &u, &v); 142 if (s[0] == 'A') 143 lct.link(u, v); 144 else 145 printf(Auto"\n", lct.query(u, v)); 146 } 147 } 148 149 int main() { 150 init(); 151 solve(); 152 return 0; 153 }
小结
LCT的时间复杂度虽然只带一个log,但是算上常数没有两个log的树链剖分快,而且树链剖分好写好调,LCT细节繁杂,所以尽量挖掘题目性质,避免盲目使用LCT(比如有些题可以线段数分治或者离线树剖就可以过)。
LCT维护链的常用套路:将一个点设为根,将另一个点access。
提取LCT中链、子树信息的时候要考虑是否提取到的信息是否是想要的(比如我经常忘记先splay)
LCT中splay操作时,最好先进行从上往下进行pushDown。我不知道为什么在旋转操作中pushDown会在一些题目蜜汁T掉。
特别感谢
ZJC
Doggu
MaxMercer
参考资料
neither_nor的讲课ppt
《QTREE解法的一些研究》 杨哲


 浙公网安备 33010602011771号
浙公网安备 33010602011771号