无旋转Treap简介
无旋转Treap是一个神奇的数据结构,能够支持插入,删除,查询k大,查询某个数的排名,查询前驱后继,支持各种区间操作和持久化。基于旋转的Treap无法实现区间反转等操作,但是无旋Treap可以轻易地支持区间操作。那为什么区间操作不用Splay而要去学无旋转Treap?原因很简单,Splay的时间复杂度是均摊的不能可持久化,而且无旋转Treap的代码量少得起飞(明明是yyf的Splay太丑了),而且无旋转Treap不容易写(翻)挂(车)。
节点
对于节点,我们通常情况下需要维护它的子树大小、随机优先级和键值(简单地说就是排序的关键字)。
由于没有旋转操作,所以不用维护父节点指针(终于可以把这个可恶的家伙扔掉了,这样至少少了10句特判),只用维护左右儿子指针就好了。
1 typedef class TreapNode { 2 public: 3 int val; 4 int pri; 5 int s; 6 TreapNode *l, *r; 7 8 TreapNode():val(0) { } 9 TreapNode(int val):val(val), pri(rand()), s(1) { } 10 11 void maintain() { 12 s = 1; 13 if(l != NULL) s += l->s; 14 if(r != NULL) s += r->s; 15 } 16 }TreapNode;
为了偷懒,我通常还会在之前加上3句话:
1 #define pnn pair<TreapNode*, TreapNode*> 2 #define fi first 3 #define sc second
分裂与合并
无旋转Treap几乎一切操作都是基于这两个操作。
首先来说说分裂操作。
分裂通常分为按权值分裂(权值小于等于x的拆成一堆,剩余的拆成另一堆),或者按排名拆分(前k大拆成一堆,其余的拆成一堆)。
很快就会出现疑问,没有像Splay一样的伸展操作,如何保证分裂出来的两堆各是一颗Treap?
虽然不能保证,但是,可以在分裂的过程中对零散的子树进行合并,最后保证两堆各是一颗Treap。
假设当前考虑到点node。我们现在只需要考虑node会和左子树一起拆成一堆还是和右子树一起拆成一堆。
现在考虑递归处理不和node拆成一堆的那颗子树。将它拆分完成后返回一个pair型变量 (lrt, rrt) ,其中 lrt 表示拆分后较小一堆的根节点和 rrt 边拆分后较大的一堆的根节点。
为了更好地说明如何合并,还是来举个例子。
我们现在要把Treap拆成权值小于等于x的两颗树,现在递归到节点node,很不幸,它的权值小于x,所以它和左子树应该被加入较小的一堆,然后我们要把权值小于等于x都拆出来,所以去递归它的右子树并返回了 (lrt, rrt) 。
现在就将node的右子树赋值为lrt,然后将lrt设为node。
对于另一种情况和按排名拆分同理。
记得在分裂的过程中维护子树大小。
1 pnn split(TreapNode* node, int val) { 2 if(node == NULL) return pnn(NULL, NULL); 3 pnn rt; 4 if(node->val <= val) { 5 rt = split(node->r, val); 6 node->r = rt.fi, rt.fi = node; 7 } else { 8 rt = split(node->l, val); 9 node->l = rt.sc, rt.sc = node; 10 } 11 node->maintain(); 12 return rt; 13 }
然后来考虑合并操作。
请记住这个合并操作的前提是其中一颗Treap上的所有键值小于另一颗Treap上的键值,否则你只能启发式合并了。
毕竟它比可并堆多了二叉查找树的性质的限制。
在学习无旋转Treap合并操作之前,先来看看左偏树的合并。
现在来效仿左偏树的合并。假设现在维护的是大根堆。加入现在考虑的两颗子树的根节点分别为a和b。
那么考虑谁的随机优先级大,谁留在当前位置,然后把其中一颗子树(至于是哪颗要根据大小来判断)和另一颗树合并,递归处理。
注意合并后返回一个根节点,要把它和当前的点连接好,然后维护子树大小。
1 TreapNode* merge(TreapNode* a, TreapNode* b) { 2 if(a == NULL) return b; 3 if(b == NULL) return a; 4 if(a->pri >= b->pri) { 5 a->r = merge(a->r, b), a->maintain(); 6 return a; 7 } 8 b->l = merge(a, b->l), b->maintain(); 9 return b; 10 }
插入与删除
对于插入操作。假设要在Treap内插入一个键值为x的点。
首先给它分配随机优先级。
然后按权值将Treap拆成键值小于等于x和大于x的两堆。
然后将插入的这个点,看成独立的一颗Treap,分别和这两颗树合并。
1 void insert(int x) { 2 TreapNode* pn = newnode(); 3 pn->val = x; 4 pnn pa = split(rt, x); 5 pa.fi = merge(pa.fi, pn); 6 rt = merge(pa.fi, pa.sc); 7 }
对于删除操作。假设要在Treap内删除一个键值为x的点。
根据上面的套路,然后按权值将Treap拆成键值小于等于x和大于x的两堆,然后再按照小于等于x - 1把前者拆成两堆,假设这三个Treap分别为\(T_{1}\),\(T_{2}\)和\(T_{3}\)。
显然\(T_{2}\)中的点的键值全是x,那么将\(T_{2}\)的左右子树合并,然后再和\(T_{1}\)和\(T_{3}\)合并,然后我们就成功删掉了一个键值为x的点。
1 void remove(int x) { 2 pnn pa = split(rt, x); 3 pnn pb = split(pa.fi, x - 1); 4 pb.sc = merge(pb.sc->l, pb.sc->r); 5 pb.fi = merge(pb.fi, pb.sc); 6 rt = merge(pb.fi, pa.sc); 7 }
其他操作
名次查询
考虑统计树中有多少个键值比查询的x小。答案是这个个数加1。
如何统计?假装要去查找这个数,如果找到了就递归左子树,每次访问右子树时计算当前点和它的左子树对答案的贡献。
1 int rank(int x) { 2 TreapNode* p = rt; 3 int rs = 0; 4 while(p) { 5 int ls = (p->l) ? (p->l->s) : (0); 6 if(x > p->val) rs += ls + 1, p = p->r; 7 else p = p->l; 8 } 9 return rs + 1; 10 }
第k小值查询
考虑要在当前子树内查询第k小值,然后递归处理,边界就是第k小值刚好是当前点或者访问到空节点(k小值不存在)
(代码详见完整代码)
各种前驱后继
和有序序列二分查找是一样的,只是二分变到了二叉搜索树上。
(代码详见完整代码)
建树
什么?建树?不是一个数一个数地往里插吗?
假如给定一个已经从小到大排好序的序列让你建树,这么做显然没有利用性质。
Solution 1 笛卡尔树式建树
考虑首先给每个点附一个随机优先级。
然后用单调栈维护最右链(现在约定它是指从根节点,一直访问右节点直到空节点形成的一条链):
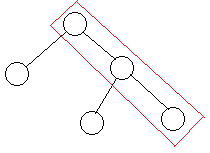
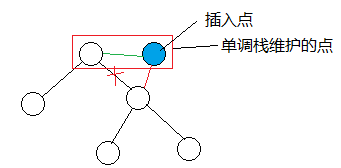
考虑在最右链末端插入下一个点,这样可能会导致出现一些点破坏堆的性质,所以我们向上找到第一个使得没有破坏堆的性质的点(由于没有记录父节点,实质上就是单调然暴力回溯),然后将它的右子树变为插入点的左子树然后将它的右子树变为插入点。
这是一个构造一个数组\(\{a_{i} = i\}\)的Treap的代码:
1 TreapNode *now, *p; 2 for(int i = 1, x; i <= n; i++) { 3 p = newnode(); 4 p->val = i; 5 now = NULL; 6 while(!s.empty() && s.top()->pri <= p->pri) { 7 now = s.top(); 8 s.pop(); 9 } 10 if(!s.empty()) 11 s.top()->r = p; 12 p->l = now; 13 s.push(p); 14 } 15 p = NULL; 16 while(!s.empty()) now = s.top(), now->r = p, p = now, s.pop(); 17 tr.rt = now;
由于用这个方法在构造时不好维护子树的大小,所以要维护子树的大小还需要写一个后序遍历:
1 void travel(TreapNode *p) { 2 if(!p) return; 3 travel(p->l); 4 travel(p->r); 5 p->maintain(); 6 }
这个方法的主旨在于装逼,没有什么特别大的作用,因为下面有个很简(智)单(障)的方法就可以完成
Solution 2 替罪羊式建树
首先可以参考替罪羊树的建树方法。
然后我们考虑如何让它满足大根堆的性质?
就让子节点的随机优先级等于父节点的随机优先级减去某个数。
或者维护小根堆,让子节点的随机优先级等于父节点的加上某个数。
上文提到的某个数是可以rand的。
虽然感觉这么做会导致一些小问题(比如某个节点一定在根),不过应该可以忽略。
感谢Doggu提供了这个方法
完整代码

1 /** 2 * bzoj 3 * Problem#3224 4 * Accepted 5 * Time: 528ms 6 * Memory: 5204k 7 */ 8 #include <bits/stdc++.h> 9 using namespace std; 10 typedef bool boolean; 11 const signed int inf = (signed) (~0u >> 1); 12 #define pnn pair<TreapNode*, TreapNode*> 13 #define fi first 14 #define sc second 15 16 typedef class TreapNode { 17 public: 18 int val; 19 int pri; 20 int s; 21 TreapNode *l, *r; 22 23 TreapNode():val(0) { } 24 TreapNode(int val):val(val), pri(rand()), s(1) { } 25 26 void maintain() { 27 s = 1; 28 if(l != NULL) s += l->s; 29 if(r != NULL) s += r->s; 30 } 31 }TreapNode; 32 33 #define Limit 200000 34 TreapNode pool[Limit]; 35 TreapNode* top = pool; 36 TreapNode* newnode() { 37 top->l = top->r = NULL; 38 top->s = 1; 39 top->pri = rand(); 40 return top++; 41 } 42 43 typedef class Treap { 44 public: 45 TreapNode* rt; 46 47 Treap():rt(NULL) {} 48 49 pnn split(TreapNode* node, int val) { 50 if(node == NULL) return pnn(NULL, NULL); 51 pnn rt; 52 if(node->val <= val) { 53 rt = split(node->r, val); 54 node->r = rt.fi, rt.fi = node; 55 } else { 56 rt = split(node->l, val); 57 node->l = rt.sc, rt.sc = node; 58 } 59 node->maintain(); 60 return rt; 61 } 62 63 TreapNode* merge(TreapNode* a, TreapNode* b) { 64 if(a == NULL) return b; 65 if(b == NULL) return a; 66 if(a->pri >= b->pri) { 67 a->r = merge(a->r, b), a->maintain(); 68 return a; 69 } 70 b->l = merge(a, b->l), b->maintain(); 71 return b; 72 } 73 74 TreapNode* find(int val) { 75 TreapNode* p = rt; 76 while(p != NULL && val != p->val) { 77 if(val < p->val) p = p->l; 78 else p = p->r; 79 } 80 return p; 81 } 82 83 void insert(int x) { 84 TreapNode* pn = newnode(); 85 pn->val = x; 86 pnn pa = split(rt, x); 87 pa.fi = merge(pa.fi, pn); 88 rt = merge(pa.fi, pa.sc); 89 } 90 91 void remove(int x) { 92 pnn pa = split(rt, x); 93 pnn pb = split(pa.fi, x - 1); 94 pb.sc = merge(pb.sc->l, pb.sc->r); 95 pb.fi = merge(pb.fi, pb.sc); 96 rt = merge(pb.fi, pa.sc); 97 } 98 99 int rank(int x) { 100 TreapNode* p = rt; 101 int rs = 0; 102 while(p) { 103 int ls = (p->l) ? (p->l->s) : (0); 104 if(x > p->val) rs += ls + 1, p = p->r; 105 else p = p->l; 106 } 107 return rs + 1; 108 } 109 110 int getkth(int r) { 111 TreapNode* p = rt; 112 while(r) { 113 int ls = (p->l) ? (p->l->s) : (0); 114 if(r == ls + 1) return p->val; 115 if(r > ls) r -= ls + 1, p = p->r; 116 else p = p->l; 117 } 118 return p->val; 119 } 120 121 int getPre(int x) { 122 TreapNode* p = rt; 123 int rs = -inf; 124 while(p) { 125 if(p->val < x && p->val > rs) rs = p->val; 126 if(x <= p->val) p = p->l; 127 else p = p->r; 128 } 129 return rs; 130 } 131 132 int getSuf(int x) { 133 TreapNode* p = rt; 134 int rs = inf; 135 while(p) { 136 if(p->val > x && p->val < rs) rs = p->val; 137 if(x < p->val) p = p->l; 138 else p = p->r; 139 } 140 return rs; 141 } 142 143 void debug(TreapNode* p) { 144 if(!p) return; 145 cerr << "(" << p->val << "," << p->pri << ")" << "{"; 146 debug(p->l); 147 cerr << ","; 148 debug(p->r); 149 cerr << "}"; 150 } 151 }Treap; 152 153 int m; 154 Treap tr; 155 156 inline void init() { 157 scanf("%d", &m); 158 } 159 160 inline void solve() { 161 int opt, x; 162 while(m--) { 163 scanf("%d%d", &opt, &x); 164 switch(opt) { 165 case 1: 166 tr.insert(x); 167 // tr.debug(tr.rt); 168 break; 169 case 2: 170 tr.remove(x); 171 break; 172 case 3: 173 printf("%d\n", tr.rank(x)); 174 break; 175 case 4: 176 printf("%d\n", tr.getkth(x)); 177 break; 178 case 5: 179 printf("%d\n", tr.getPre(x)); 180 break; 181 case 6: 182 printf("%d\n", tr.getSuf(x)); 183 break; 184 } 185 } 186 } 187 188 int main() { 189 srand(233u); 190 init(); 191 solve(); 192 return 0; 193 }


