Burnside定理学习笔记
Burnside定理主要用于解决这样一类问题,用n种颜色为一个物体着色,当一种着色通过一些变换得到的另一种着色,我们认为它们是用一种着色,求本质不同的着色方案。(详细的适用条件将在下文阐述)
现在用一个简简单单为问题进行引入,用红色和蓝色两种颜色对一个正五边形进行染色,如果两种染色可以通过旋转或者翻转使得它们一样,那么我们认为它们是相同的染色方案,问本质不同的染色方案数。
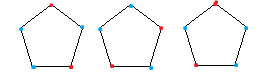
例如我们认为这三种着色是相同的,因为第一个五边形通过向右旋转72°可以得到第二个五边形,或者沿着最上面的顶点到其对边的垂线所在直线翻转就可以得到第三个五边形。
- 从这里开始
置换与置换群
->置换
置换,通俗地来讲就是一个将1到n一一映射到1到n的一个函数,在《组合数学》上用\(2 \times n\)的阵列来表示这个置换。例如
\(\left ( \begin{matrix}1 & 2 & 3 & \cdots & n \\ i_{1} & i_{2} & i_{3} & \cdots & i_{n}\end{matrix} \right )\)
在\(i_{1}, i_{2}, i_{3},\cdots,i_{n}\)中没有重复的数,且都是1到n的整数。
若
\(f = \left ( \begin{matrix}1 & 2 & 3\\ 3 & 1 & 2 \end{matrix} \right )\)
则有\(f\left ( 1 \right ) = 3, f\left(2 \right ) = 1,f\left (3 \right ) = 2\)。
对于两个置换\(f,g\),定义它们的合成运算
\(\left ( f \circ g \right )\left ( x \right ) = f\left ( g\left ( x \right ) \right )\)
例如
\(\left (\begin{matrix}1 & 2 & 3 \\ 3 & 1 & 2\end{matrix} \right )\circ \left ( \begin{matrix}1 & 2 & 3 \\ 2 & 1 & 3\end{matrix} \right )=\left ( \begin{matrix}1 & 2 & 3 \\ 3 & 2 & 1\end{matrix} \right )\)
\(\left ( \begin{matrix}1 & 2 & 3\\ 2 & 1 & 3 \end{matrix} \right )\circ\left(\begin{matrix}1 & 2 & 3 \\ 3 & 1 & 2 \end{matrix} \right )=\left(\begin{matrix}1 & 2 & 3\\1 & 3 & 2 \end{matrix} \right )\)
由此可见,置换的合成运算不满足交换律。但是可以验证置换的运算满足结合律。
通常用幂运算来定义一个置换和自己的合成运算,例如
\(f^{1} = f,f^{2}=f\circ f ,f^{3}=f\circ f\circ f\)
恒等置换是指\(\{1, 2, 3, \cdots, n\}\)中的各整数映射到它自身的一个置换,即
\(\iota \left ( k \right )=k\ \ \ \ \left(k = 1, 2, 3, \cdots, n\right)\)
它等价于
\(\iota = \left(\begin{matrix} 1 & 2 & 3 &\cdots & n \\ 1 & 2 & 3 &\cdots & n \end{matrix} \right )\)
对于恒等置换有这样的性质
\(f\circ \iota = \iota \circ f = f\)
定义置换\(f\)的逆函数\(f^{-1}\)使得
\(f\circ f^{-1} = \iota\)
->置换群
令定义在1~$n$上的所有置换组成的集合为$S_{n}$
对于它的一个非空子集$G$,如果它满足:
- 对合成运算的封闭性:对于任意$f,g\in G$,则$f\circ g\in G$
- 存在单位元:$S_{n}$中的恒等置换$\iota \in G$
- 对逆元的封闭性:若$f \in G$,则$f^{-1} \in G$
现在来证明对于每一个置换群都满足消去律:
若$f,g,h\in G$,$f\circ g = f\circ h$意味着$g = h$
证明
$f\circ g = f\circ h$
$f^{-1} \circ \left( f\circ g\right ) = f^{-1}\circ \left( f\circ h\right )$
$\left( f^{-1} \circ f\right )\circ g = \left(f^{-1}\circ f\right )\circ h$
$\iota \circ g = \iota \circ h$
$g = h$
着色
假设现在有一个$n$边形,它的$n$个顶点的标号分别为1~$n$的整数,并且它的每一个顶点都有一个颜色。现在用
$\mathbf{c}=\left(c_{1},c_{2}, c_{3}, \cdots, c_{n}\right )$
来表示它的着色方案,其中$c_{i}$表示顶点标号为i的颜色。
说得很抽象,来举个栗子:
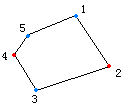
如果用R表示红色,B表示蓝色,那么这个多边形的着色方案可以表示为$\mathbf{c}=\left(B,R,B,R,B\right )$。
现在来定义置换对着色的作用:
对于$G$中的一个置换$f$和一种着色方案$\mathbf{c}$,那么定义$f$对着色$\mathbf{c}$作用的结果为$f \ast \mathbf{c}$ ,它满足$\left(f\ast \mathbf{c} \right )\left( x\right ) = c_{f^{-1}\left(x \right )}$
简单地说,就是将点$f^{-1}\left(x \right)$的颜色移动到点$x$上(说成将点$x$上的颜色移动到点$f\left(x\right)$也是一样的)。
例如将置换$f = \left ( \begin{matrix}1 & 2 & 3 & \cdots & n - 1 & n\\ 2 & 3 & 4 & \cdots & n & 1 \end{matrix} \right )$作用在上面五边形着色方案的例子上的结果为:
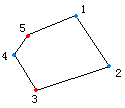
$\mathbf{c}=\left(B,B,R,B,R\right )$
另外有关置换的合成运算和置换对着色的作用的两个运算之间满足下面关系:
$\left(f\circ g \right )\ast \mathbf{c}=f\ast\left(g\ast \mathbf{c} \right )$
等式的左边在干的事情就是将点$x$上的颜色移动到点$\left(f\circ g \right )\left(x\right)$上。再来考虑右边,它先将点$x$上的颜色移动到点$g\left ( x \right )$,然后移动到$f\left (g\left ( x \right ) \right )$。然后可以开心地发现这两玩意儿是等价的。
Burnside定理
在了解Burnside定理之前,我们首先明确一些定义:
-
等价着色:在置换群$G$的作用下,我们称两种着色$\mathbf{c}_{1},\mathbf{c}_{2}$是指,存在一个$f\in G$使得$f\ast \mathbf{c}_{1} = \mathbf{c}_{2}$
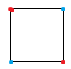
例如上图,在置换$f=\left(\begin{matrix}1 & 2 & 3 & 4 \\ 3 & 4 & 1 & 2 \end{matrix} \right )$的作用下,会使得它的着色方案不会改变。
- 约定若$G$为置换群,则$G\left(\mathbf{c}\right)=\left\{f:f\in G\wedge f\ast \mathbf{c} = \mathbf{c}\right\}$(小科普:$\wedge$是合取符号,它的意思是并且)。通俗地讲$G\left(\mathbf{c}\right)$就是$G$中作用在着色方案$\mathbf{c}$上仍与原来着色方案等价的置换组成的集合。
- 约定$C$表示由可行的着色方案组成的集合,且满足对于任意$f\in G,\mathbf{c} \in C$,都有$f\ast \mathbf{c} \in C$。
- 约定$C\left(f \right )=\left\{\mathbf{c}:\mathbf{c}\in C\wedge f\ast \mathbf{c} = \mathbf{c}\right\}$。通俗地讲$C\left(f \right )$就是置换$f$作用在着色集合$C$中的着色方案,使其不变的着色方案构成的集合。
- 约定$E\left(\mathbf{c} \right )=\left\{f\ast \mathbf{c}:f\in G \right \}$。通俗地讲,就是在置换群$G$中的置换的作用下,与着色方案$c$等价的着色集合。
- 约定$N\left(G,C \right )$表示在置换群$G$中的置换的作用下,着色集合$C$中不等价的着色方案数。
一些该扯的定义和约定扯完了,终于可以开始步入正题了!(前面一大篇干什么去了?)
引理1 如果置换$f$作用在着色方案$\mathbf{c}$上,使其不变,那么它的逆函数也会使其不变。
证明 因为有$f\ast \mathbf{c} = \mathbf{c}$,所以:
$\left (f^{-1}\circ f \right )\ast \mathbf{c} = \mathbf{c}$(恒等置换一定使着色方案不变)
$f^{-1}\ast \left (f \ast \mathbf{c} \right ) = \mathbf{c}$
$f^{-1}\ast \mathbf{c}= \mathbf{c}$
然后说明一下$G\left(\mathbf{c}\right)$是置换群。
- 单位元:因为$G$是置换群,又因为恒等置换会使得着色方案不会改变,所以$\iota \in G\left ( \mathbf{c} \right )$。
- 对合成运算的封闭:因为如果置换$f,g$能够使得某着色方案不变,根据合成和作用运算的关系易证
- 对逆函数的封闭:根据引理1易证
定理1 若$G$为置换群,对于$G$中任意置换$f,g$,和任意一种着色方案$\mathbf{c}\in C$,若有$f\ast \mathbf{c} = g\ast \mathbf{c}$,当且仅当$\left (f^{-1}\circ g \right )\in G\left(\mathbf{c} \right )$。
证明 假设$f\ast \mathbf{c} = g\ast \mathbf{c}$,那么有:
$\left (f^{-1}\circ g \right ) \ast \mathbf{c} = f^{-1}\ast \left(g\ast \mathbf{c} \right )=f^{-1}\ast \left (f\ast \mathbf{c} \right )=\left(f^{-1}\circ f \right )\ast \mathbf{c} = \mathbf{c}$
所以当$f\ast \mathbf{c} = g\ast \mathbf{c}$时,$\left (f^{-1}\circ g \right )\in G\left(\mathbf{c} \right )$。
假设$\left (f^{-1}\circ g \right )\in G\left(\mathbf{c} \right )$,那么有:
$f\ast \mathbf{c} = f\ast \left [\left(f^{-1}\circ g\right) \ast\mathbf{c} \right ]=g\ast \mathbf{c}$
所以$f\ast \mathbf{c} = g\ast \mathbf{c} \Leftrightarrow \left (f^{-1}\circ g \right )\in G\left(\mathbf{c} \right )$
根据这个定理,可以得到下面这个定理(又称为轨道-稳定集定理)
定理2 若$G$为置换群,则有$\left |E\left(\mathbf{c}\right) \right |=\frac{\left |G \right |}{\left |G\left(\mathbf{c} \right ) \right |}$
证明 考虑对于任意$f \in G$,若存在一个$g \in G$使得:
$f \ast \mathbf{c} = g\ast \mathbf{c}$
根据定理1可以得到:
$f^{-1}\circ g\in G\left ( \mathbf{c} \right )$
又因为消去律存在,所以可能的$g$的个数就是$\left |G\left ( \mathbf{c} \right ) \right |$
对于每个置换$f$,都存在恰好$\left |G\left ( \mathbf{c} \right ) \right |$个置换,使得作用在$\mathbf{c}$上与它等价,又因为总共有$\left |G \right |$个置换。再根据$|E\left(\mathbf{c}\right)| $的定义,不难得到:
$\left |E\left(\mathbf{c}\right) \right |=\frac{\left |G \right |}{\left |G\left(\mathbf{c} \right ) \right |}$
然后就是要介绍的主题Burnside定理。
定理3 若$G$是置换群,$C$是满足对于任意$f\in G,\mathbf{c}\in C$,都有$f\ast \mathbf{c}\in C$,则在置换群$G$的作用下,$C$中非等价着色方案数为
$N\left(G,C \right )=\frac{1}{\left |G \right |}\sum_{f\in G}\left | C\left ( f \right ) \right |$
证明 考虑对使得$f\ast \mathbf{c} = \mathbf{c}$的二元组$\left ( f,\mathbf{c} \right )$进行计数。
第一种计数方法是枚举$f$,然后不难得到它的数量为:
$\sum_{f\in G}\left|C\left(f \right )\right|$
第二种计数方法是枚举$\mathbf{c}$,那么显然又有:
$\sum_{\mathbf{c}\in C}\left|G\left(\mathbf{c} \right )\right|$
于是就有:
$\sum_{f\in G}\left|C\left(f \right )\right|=\sum_{\mathbf{c}\in C}\left|G\left(\mathbf{c} \right )\right|=\sum_{\mathbf{c}\in C}\frac{\left |G \right |}{\left |E\left ( \mathbf{c} \right ) \right |}$
然后可以得到
$\frac{1}{\left |G \right |}\sum_{f\in G}\left|C\left(f \right )\right|=\sum_{\mathbf{c}\in C}\frac{1}{\left |E\left ( \mathbf{c} \right ) \right |}$
再来考虑等式右边的意义,对于每个等价的着色方法,对和的贡献都为$\frac{1}{\left |E\left ( \mathbf{c} \right ) \right |}$,于是可以得出对于每种等价的作色方案对和的总贡献为1,于是整理式子,得到我们想要的东西
$N\left(G,C \right )=\frac{1}{\left |G \right |}\sum_{f\in G}\left | C\left ( f \right ) \right |$
请记住,Burnside定理的使用对置换集$G$和着色集$C$均有限制,不能乱用。
建议不要只记结论,应该理解它,并学会推导的方法。
小练习
现在来思考思考引入中给的小问题。
对于旋转变换,每个旋转变换都可以表示成$\rho_{5} ^{k}$的形式,我们约定:
$\rho_{n} = \left(\begin{matrix}1 & 2 & 3 & \cdots & \left(n - 1 \right ) & n\\ 2 & 3 & 4 & \cdots & n & 1 \end{matrix} \right )$
对于每个翻转变换显然也是可以用置换$\tau_{i}$来表示的。
显然,在所有旋转操作和翻转操作的置换构成的集合中存在单位元,对逆元封闭(显然转过来,还可以转回去,转回去的置换就是它的逆函数,对于翻转同理),对结合运算封闭(请自行领会),所以它构成了置换群。
然后来考虑着色集合是否满足条件。显然满足(难道我旋转一下或者翻转一下就不合法了?)。
然后就可以考虑Burnside定理。
考虑所有旋转操作,当$i = 0$时,就是恒等置换,无论什么着色都不会改变,所以$\left|C\left(\rho_{5}^{0}\right)\right| = 2^{5} = 32$(每个顶点颜色任意选)。当$i = 1,2,3,4$时,手动模拟一下(或者手写个dfs),可以发现所有顶点颜色都必须一样才会使得在这些旋转置换下不会改变着色。所以有:
$\left |C\left(\rho_{5}^{i} \right ) \right | =\left\{\begin{matrix}32\ \ \ \ \ \ \ \ \ \ \ \ \left(i = 0 \right )\\ 2\ \ \ \ \ \left(i = 1,2,3,4 \right )\\ \end{matrix}\right.$
考虑所有翻转操作,对称轴穿过的顶点可以任意选,其他点的颜色只能和翻转后到的点的颜色一样才能使得在翻转置换的作用下不会改变着色。所以
$\left |C\left ( \tau _{i} \right ) \right |=2^{3}=8$
所以,不等价的着色方案数是
$N\left(G, C \right )=\frac{1}{2 \times 5}\left(32 + 2 \times 4 + 8\times 5 \right )=8$
但是对于OI中的Burnside定理的应用就不会这样友好了,比如我们来看一道入门题(水题)
题目大意 有$n$种颜色的珠子,每种珠子有无限多个,串成长度为$n$的项链,两种项链如果可以通过旋转使得它们相同,那么我们认为它们是同一种项链,问本质不同的项链数,答案模$P$输出。总共有$T$组询问,每组询问的$P$可能不同。
Subtask 1(我自己加的qaq) $\sum n\leqslant 5\times 10^{5}$
对于所有旋转操作的置换可以按照上面的方式进行表示。
易证,这个置换集合$G$是置换群。同理,染色集合$C$也是满足条件的。
好,现在我们要求在每种旋转操作的置换的作用下,不变的染色方案数。
dfs(T了)?打表(很有耐心。。我想用天河二号来做这个任务估计100年后都还完成不了。)?手动模拟(要求不高,你可以试试先画出$10^{5}$边形)?
看来只能想办法优化了。下面给出一个定理和可能存在问题的证明
定理4 若$C$是由所有k种颜色构成的着色集,对一个环进行染色,那么
$\left |C\left ( \rho_{n}^{i} \right ) \right |=k^{(i,n)}\ \ \ \ \left(i = 0, 1, 2, \cdots,n - 1 \right )$
证明 考虑和 $x$ 颜色必须相同的位置 $y$ 满足,存在 $t$ 使得 $x + ti \equiv y \pmod{n}$。
这个方程有解当且仅当 $x \equiv y \pmod{(n, i)}$。
所以存在 $(n, i)$ 个等价类。
回到原问题,直接带公式,得到答案
$ans = \frac{1}{n}\sum_{i = 0}^{n - 1}n^{\left(i, n \right )}$
时间复杂度$\Theta \left ( n\log n \right )$。
Subtask 2 (原题) $1\leqslant n\leqslant 10^{9},1\leqslant T\leqslant 3500$
这数据范围很不友善啊。。
有注意到$\left(i,n \right )$的取值一定是$n$的约数,所以至多$\Theta \left ( \sqrt{n} \right )$种取值,于是可以考虑枚举$n$的约数。于是得到了,
$\frac{1}{n}\sum_{d|n}n^{d}\sum_{i = 1}^{n}\left [ \left ( i, n \right ) = d\right ]1\\=\sum_{d|n}n^{d-1}\sum_{i = 1}^{n}\left [ \left ( \frac{i}{d}, \frac{n}{d} \right ) = 1\right ]1\\=\sum_{d|n}n^{d-1}\varphi \left ( \frac{n}{d} \right )$
对于欧拉函数可以用线性筛预处理出1 ~ $\sqrt{n}$内的欧拉函数值,对于大于$\sqrt{n}$的约数,可以考虑用欧拉函数值的计算公式去做。
总时间复杂度O(能过)。
Code

1 /** 2 * poj 3 * Problem#2154 4 * Accepted 5 * Time: 1204ms 6 * Memory: 860k 7 */ 8 #include <iostream> 9 #include <algorithm> 10 #include <cstdio> 11 using namespace std; 12 typedef bool boolean; 13 14 const int lim = 32001; 15 int num; 16 int pri[10000]; 17 int phi[lim]; 18 boolean vis[lim]; 19 inline void Euler() { 20 fill(vis + 1, vis + lim, false); 21 vis[1] = true, phi[1] = 1; 22 for(int i = 2; i < lim; i++) { 23 if(!vis[i]) pri[num++] = i, phi[i] = i - 1; 24 for(int j = 0, x; j < num && pri[j] * i < lim; j++) { 25 x = pri[j] * i; 26 vis[x] = true; 27 if(i % pri[j]) 28 phi[x] = phi[i] * (pri[j] - 1); 29 else { 30 phi[x] = phi[i] * pri[j]; 31 break; 32 } 33 } 34 } 35 } 36 37 int T; 38 int n, P; 39 40 inline void init() { 41 scanf("%d%d", &n, &P); 42 } 43 44 int qpow(int a, int pos) { 45 int rt = 1, pa = a; 46 for(; pos; pos >>= 1, pa = (pa * 1ll * pa) % P) 47 if(pos & 1) 48 rt = (rt * 1ll * pa) % P; 49 return rt; 50 } 51 52 int Phi(int n) { 53 if(n < lim) return phi[n]; 54 int x = n, rt = 1; 55 for(int i = 0; pri[i] * pri[i] <= n && x > 1; i++) 56 if(!(x % pri[i])) { 57 rt *= pri[i] - 1, x /= pri[i]; 58 while(!(x % pri[i])) rt *= pri[i], x /= pri[i]; 59 } 60 if(x > 1) rt *= x - 1; 61 return rt; 62 } 63 64 inline void solve() { 65 int res = 0; 66 for(int i = 1; i * i <= n; i++) { 67 if(!(n % i)) { 68 res = (res + qpow(n, i - 1) * 1ll * Phi(n / i)) % P; 69 if(i * i != n) 70 res = (res + qpow(n, n / i - 1) * 1ll * Phi(i)) % P; 71 } 72 } 73 printf("%d\n", res); 74 } 75 76 int main() { 77 Euler(); 78 scanf("%d", &T); 79 while(T--) { 80 init(); 81 solve(); 82 } 83 return 0; 84 }
小结&后话
Burnside定理用于解决在置换群中置换的作用下不等价的着色方案数这么一类问题。
通常主要难点集中于求在置换$f$的作用下等价的着色方案数。
这一部分主要的处理方法:有公式、动态规划、矩阵快速幂 + 动态规划等等
参考资料
《组合数学》 (美)Richard A. Brualdi
特别鸣谢
idy002
MaxMercer
jerome_wei

