bzoj 3522 / 4543 [POI 2014] Hotel - 动态规划 - 长链剖分
题目传送门
题目大意
给定一棵树,问有多少个无序三元组$(x, y, z)$使得这三个不同点在树上两两距离相等。
考虑这三个点构成的虚树。选取一个"舒适"的计数对象。
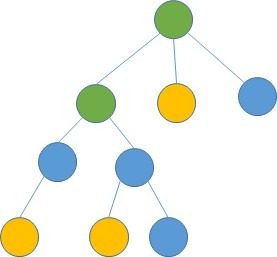
其中黄色的点是关键点,绿色的点是虚树上的虚点。
在树形动态规划的时候通常考虑一个点子树内的情况会比较简单。因此考虑将计数对象设为虚树上最浅的一个点。
性质1 最近公共祖先深度较深的两点到它们的最近公共祖先的距离相等。
证明 设这两点为$A, B$,第三点为$C$。当三个点的最近公共祖先相同时显然。否则第三点到这两点距离不相等。
当三个点的最近公共祖先不相同时。设$A$和$B$两点的最近公共祖先为$D$。
因为三个点公共祖先不同所以$C$在$D$的子树外。
此时虚树上有5个点,因为$A$和$C$、$B$和$C$的最近公共祖先是相同点,设它为$E$。
那么有$dis(A, D) + dis(D, E) + dis(E, C) = dis(B, D) + dis(D, E) + dis(E, C)$
所以$dis(A, D) = dis(B, D)$。
用$f[i][j]$表示在$i$的子树中,到点$i$距离为$j$的点的个数。
如果点$x, y$的LCA的深度为$d$,且它们到它们的LCA的距离相等,$g[i][j]$表示在$i$的子树中,有多少个点对$(x, y)$使得它们的LCA到点$i$的距离为$d - j$。
为了避免算重,应当边在合并子树的信息的时候边计算答案。
除了$f[i][0]$初始为1,其他初始为0。
设$i$的某个子节点为$k$。那么转移有(顺序不是这样的):
$f[i][j] = f[i][j] + f[k][j - 1]$
$g[i][j] = g[i][j] + g[k][j + 1]$
$g[i][j] = g[i][j] + f[i][j] * f[k][j - 1]$ (当前点是较深的LCA)
$result = result + f[i][j] * g[k][j - 1] + g[i][j] * f[k][j + 1]$
于是状态$O(n^{2})$,时间复杂度也是满满的$O(n^{2})$。成功爆炸。
注意到前两个转移只是挪一挪指针,而初始的时候$f, g$几乎可以看成没有值。因此这一部分考虑直接通过指针赋值来实现$O(1)$转移。
问题是,这个只能做一次。那就选择深度最深的子树进行转移。
性质2 该种做法时间复杂度$O(n)$。
证明 对树进行长链剖分。当且仅当一条边是虚边的时候需要暴力进行转移,时间复杂度是这棵子树的深度。
这个深度的意义可以看成虚边深的一端连接的长链的长度。因为长链一直连向叶子结点,中间不会有其他虚边。
又因为长链覆盖整棵树。因此时间复杂度$O(n)$。
然后开一个内存池动态分配空间。(其实直接new也是可以的,只是慢一点)。
Code
1 /** 2 * bzoj 3 * Problem#3522 & 4543 4 * Accepted & Accepted 5 * Time: 44ms & 768ms 6 * Memory: 19652k & 21900k 7 */ 8 #include <iostream> 9 #include <cassert> 10 #include <cstdlib> 11 #include <cstdio> 12 #include <vector> 13 #ifndef WIN32 14 #define Auto "%lld" 15 #else 16 #define Auto "%I64d" 17 #endif 18 using namespace std; 19 typedef bool boolean; 20 #define ll long long 21 22 const int N = 100005; 23 24 ll pool[20 * N]; 25 ll* top = pool; 26 27 ll* alloc(int len) { 28 ll* rt = top; 29 top += len; 30 return rt; 31 } 32 33 int n; 34 ll res = 0; 35 vector<int> mg[N]; 36 int ml[N], longs[N]; 37 ll *f[N], *g[N]; 38 39 inline void init() { 40 scanf("%d", &n); 41 for (int i = 1, u, v; i < n; i++) { 42 scanf("%d%d", &u, &v); 43 mg[u].push_back(v); 44 mg[v].push_back(u); 45 } 46 } 47 48 void dfs1(int p, int fa) { 49 ml[p] = 0; 50 int maxl = -1, id = -1; 51 for (int i = 0; i < (signed) mg[p].size(); i++) { 52 int e = mg[p][i]; 53 if (e == fa) continue; 54 dfs1(e, p); 55 ml[p] = max(ml[p], ml[e] + 1); 56 if (ml[e] > maxl) 57 maxl = ml[e], id = e; 58 } 59 longs[p] = id; 60 } 61 62 void dfs2(int p, int fa, int& maxlen, int blank) { 63 maxlen = max(maxlen, ml[p]); 64 if (longs[p] != -1) { 65 dfs2(longs[p], p, maxlen, blank + 1); 66 res += g[longs[p]][1]; 67 f[p] = f[longs[p]] - 1, f[p][0] = 1; 68 g[p] = g[longs[p]] + 1; 69 } else { 70 f[p] = alloc(maxlen + 5 + blank) + blank; 71 g[p] = alloc(maxlen + 5 + blank); 72 f[p][0] = 1; 73 } 74 75 for (int i = 0; i < (signed) mg[p].size(); i++) { 76 int e = mg[p][i], mxlen = 0; 77 if (e == fa || e == longs[p]) continue; 78 dfs2(e, p, mxlen, 0); 79 // assert(f[p] + ml[e] + 1 < org[p] + siz[p]); 80 for (int j = 0; j < ml[e]; j++) 81 res += f[p][j] * g[e][j + 1]; 82 for (int j = 1; j <= ml[e] + 1; j++) 83 res += g[p][j] * f[e][j - 1]; 84 for (int j = 1; j <= ml[e] + 1; j++) 85 g[p][j] += f[p][j] * f[e][j - 1]; 86 for (int j = 0; j <= ml[e]; j++) 87 f[p][j + 1] += f[e][j]; 88 for (int j = 1; j <= ml[e]; j++) 89 g[p][j - 1] += g[e][j]; 90 } 91 } 92 93 inline void solve() { 94 int mxlen = 0; 95 dfs1(1, 0); 96 dfs2(1, 0, mxlen, 0); 97 printf(Auto, res); 98 } 99 100 int main() { 101 init(); 102 solve(); 103 return 0; 104 }

 浙公网安备 33010602011771号
浙公网安备 33010602011771号