bzoj 4585 烟火表演 - 动态规划 - 可并堆
当前正在考虑某个节点,设$f(x)$表示算上它到父节点的边,后将所有叶节点到它的父节点的距离改为$x$的最小代价。设$g(x)$表示将它所在的子树内的所有叶节点到它的距离改为$x$的最小代价,它和它父节点的边的边权为$w$。
对于一个点的各个子树之间互相独立,所以这个点的$g$函数相当于,它的各个子节点的$f$函数值的和。
$g(x) = \sum_{y\in son(x)}f_{y}(x)$
对于$f$函数,我们需要做决策:
$f(x) = \min_{0\leqslant y\leqslant x}\left \{ g(y) + \left | w - (x - y) \right | \right \}$
这等价于将每个位置$x$,考虑它前面位置的$g$函数值,和函数$h(y) = \left | w - (x - y) \right |$的和,然后取一个最小值作为$f(x)$。
于是就懵逼。值域可能很大,数组也开不下,所以怎么办呢?
考虑这个函数图像具有的性质。
首先考虑叶节点的$f$函数(它的$g$函数没有意义)。它是一条优美的绝对值函数的图像:
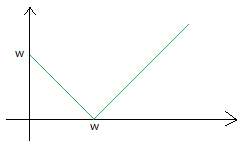
然后在考虑它的父节点,它的父节点的$g$函数将若干个这样的函数加在了一起。因为旧函数的导函数递增,新函数的导函数也等于旧函数导函数的和,所以新函数斜率递增。
而且这个函数图像非常特殊,每遇到一个拐点,导函数的值加1。
它的父节点的$g$函数可能会长成下面这个样子(这图画得很不标准):
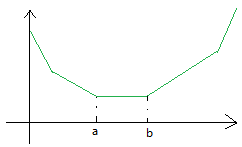
它一定会出现平着的一段区间$[a, b]$。然后分类讨论一下它变换到$f$函数。

当$0\leqslant x \leqslant a$时,显然$f(x)$的决策点取$x$最优。
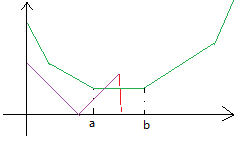
当$a < x \leqslant a + w$时,显然$f(x)$的决策点取$a$最优。
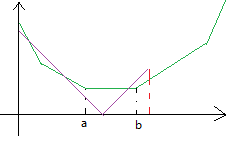
当$a + w < x \leqslant b + w$时,显然$f(x)$的最优决策点取$x - w$。

当$x > b + w$时,决策点取$b$。
所以整理一下式子不难得到:
$f(x) = \left\{\begin{matrix}g(x) + w \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (0\leqslant x \leqslant a)\\ g(a) + w - x + a \ (a < x \leqslant a + w)\\ g(x - w) \ \ \ \ \ \ (a + w < x \leqslant b + w)\\ g(b) + x - b - w \ \ \ \ \ \ \ (x > b + w)\end{matrix}\right.$
这有什么用呢?
考虑它的图像的变化:
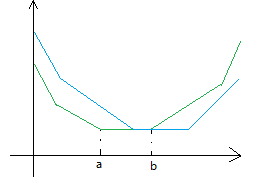
它相当于将平的一段向右移动了$w$个单位,然后将$[0, a]$的函数图像向上平移了$w$个单位,中间空的一段补斜率为-1的线段。
然后把$[b, +\infty )$的图像变成斜率为1的射线。
这样新函数的图像也是一个满足刚刚提到的两点性质的下凸壳,不难证明所有非叶节点的$f, g$函数都满足这样的性质。
因此,我们考虑用某个数据结构来维护拐点集合。
所以我们可以平衡树 + 启发式合并来做这道题。于是这样就被卡掉了。
所以怎么办呢?实际上,我并不需要维护一个完全有序的序列,我只要支持:
- 弹掉最大的某几个。
- 支持插入元素
- 支持快速合并
因为被弹掉的元素一去不复返,可以暴力弹掉它们,因此可以想到可并堆。
这样时间复杂度降为$O((n + m)\log (n + m))$。
Code
1 /** 2 * bzoj 3 * Problem#4585 4 * Accepted 5 * Time: 8736ms 6 * Memory: 18872k 7 */ 8 #include <iostream> 9 #include <cassert> 10 #include <cstdlib> 11 #include <cstring> 12 #include <cstdio> 13 #ifndef WIN32 14 #define Auto "%lld" 15 #else 16 #define Auto "%I64d" 17 #endif 18 using namespace std; 19 typedef bool boolean; 20 21 #define ll long long 22 const int N = 6e5 + 5; 23 24 typedef class SkewNode { 25 public: 26 ll val; 27 SkewNode *l, *r; 28 29 SkewNode() { } 30 }SkewNode; 31 32 SkewNode pool[N]; 33 SkewNode* top = pool; 34 35 SkewNode* newnode(int val) { 36 top->val = val; 37 return top++; 38 } 39 40 SkewNode* merge(SkewNode* a, SkewNode* b) { 41 if (!a || !b) return (a) ? (a) : (b); 42 if (a->val < b->val) swap(a, b); 43 a->r = merge(a->r, b); 44 swap(a->l, a->r); 45 return a; 46 } 47 48 int n, m; 49 int *fa, *cs, *ss, *ks; 50 ll *bs; 51 SkewNode** rs; 52 53 inline void init() { 54 scanf("%d%d", &n, &m); 55 n += m; 56 bs = new ll[(n + 1)]; 57 fa = new int[(n + 1)]; 58 cs = new int[(n + 1)]; 59 ss = new int[(n + 1)]; 60 ks = new int[(n + 1)]; 61 rs = new SkewNode*[(n + 1)]; 62 memset(bs, 0, sizeof(ll) * (n + 1)); 63 memset(ks, 0, sizeof(int) * (n + 1)); 64 memset(ss, 0, sizeof(int) * (n + 1)); 65 memset(rs, 0, sizeof(SkewNode*) * (n + 1)); 66 for (int i = 2; i <= n; i++) 67 scanf("%d%d", fa + i, cs + i); 68 } 69 70 inline void solve() { 71 for (int i = n - m + 1; i <= n; i++) { 72 int f = fa[i]; 73 ss[f] += 2, ks[f] += 1, bs[f] += cs[i]; 74 rs[f] = merge(rs[f], newnode(cs[i])); 75 rs[f] = merge(rs[f], newnode(cs[i])); 76 } 77 for (int i = n - m; i > 1; i--) { 78 while (ss[i] > ks[i] + 1) ss[i]--, rs[i] = merge(rs[i]->l, rs[i]->r); 79 SkewNode *a = rs[i], *b = rs[i] = merge(rs[i]->l, rs[i]->r); 80 bs[i] += cs[i], a->val += cs[i], b->val += cs[i], a->l = a->r = NULL; 81 rs[i] = merge(rs[i], a); 82 int f = fa[i]; 83 bs[f] += bs[i], ks[f] += ks[i], ss[f] += ss[i]; 84 rs[f] = merge(rs[f], rs[i]); 85 } 86 while (ss[1] > ks[1]) ss[1]--, rs[1] = merge(rs[1]->l, rs[1]->r); 87 ll res = bs[1]; 88 while (rs[1]) 89 res -= rs[1]->val, rs[1] = merge(rs[1]->l, rs[1]->r); 90 printf(Auto"\n", res); 91 } 92 93 int main() { 94 init(); 95 solve(); 96 return 0; 97 }
