bzoj 2115 Xor - 线性基 - 贪心

题目传送门

　　这是个通往vjudge的虫洞

　　这是个通往bzoj的虫洞

题目大意

　　问点$1$到点$n$的最大异或路径。

　　因为重复走一条边后，它的贡献会被消去。所以这条路径中有贡献的边可以看成是一条$1$到$n$的简单路径加上若干个环。

　　因此可以找任意一条路径，然后找出所有环扔进线性基跑出最大异或和。

　　但是找出所有环可能会T掉，但是仔细画图发现，并不需要找出所有环，例如：

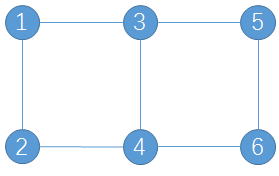
　　在上图中，你并不需找出所有的环，只用找出1 - 3 - 4 - 2和3 - 5 - 6 - 4这两个环，它们异或后就能得到环1 - 3 - 5 - 6 - 4 - 2。

　　至于找这个环，可以用dfs生成树来找。当出现返祖边的时候就意味着找到了一个环。

　　然后可以记一个异或的前缀和，这样就可以$O(1)$算出环上的边权的异或和。

　　对于任意一条路径得到的异或和如果为$s$，那么我们只需要考虑线性基的每一位上，如果异或上它，能够使答案变大，就异或上它。

　　因为线性基不能保证最大的异或和由之前扔进去的所有数得到，所以必须这么贪一下心。

　　这样的正确性显然。

Code

  1 /** 
  2  * bzoj
  3  * Problem#2115
  4  * Accepted
  5  * Time: 740ms
  6  * Memory: 7040k
  7  */ 
  8 #include <bits/stdc++.h>
  9 #ifndef WIN32
 10 #define Auto "%lld"
 11 #else
 12 #define Auto "%I64d"
 13 #endif
 14 
 15 using namespace std;
 16 typedef bool boolean;
 17 
 18 #define ll long long
 19 
 20 typedef class LinearBasis {
 21     public:
 22         ll b[64];
 23 
 24         LinearBasis() {    }
 25 
 26         void insert(ll x) {
 27             for (int i = 62; ~i; i--) {
 28                 if (x & (1ll << i))    x ^= b[i];
 29                 if (x & (1ll << i)) {
 30                     b[i] = x;
 31                     for (int j = i - 1; ~j; j--)
 32                         if (b[i] & (1ll << j))
 33                             b[i] ^= b[j];
 34                     for (int j = i + 1; j <= 62; j++)
 35                         if (b[j] & (1ll << i))
 36                             b[j] ^= b[i];
 37                     break;
 38                 }
 39             }
 40         }
 41 
 42         ll getAns(ll ans) {
 43             for (int i = 0; i <= 62; i++)
 44                 if ((ans ^ b[i]) > ans)
 45                         ans ^= b[i];
 46             return ans;
 47         }
 48 }LinearBasis;
 49 
 50 typedef class Edge {
 51     public:
 52         int end, next;
 53         ll w;
 54 
 55         Edge(int end = 0, int next = 0, ll w = 0):end(end), next(next), w(w){    }
 56 }Edge;
 57 
 58 typedef class MapManager {
 59     public:
 60         int ce;
 61         int *h;
 62         Edge* es;
 63 
 64         MapManager() {    }
 65         MapManager(int n, int m):ce(0) {
 66             h = new int[(n + 1)];
 67             es = new Edge[(m + 1)];
 68             memset(h, 0, sizeof(int) * (n + 1));
 69         }
 70 
 71         void addEdge(int u, int v, ll w) {
 72             es[++ce] = Edge(v, h[u], w);
 73             h[u] = ce;
 74         }
 75 
 76         Edge& operator [] (int p) {
 77             return es[p];
 78         }
 79 }MapManager;
 80 
 81 int n, m;
 82 ll *xs;
 83 MapManager g;
 84 LinearBasis lb;
 85 boolean *vis;
 86 
 87 inline void init() {
 88     scanf("%d%d", &n, &m);
 89     xs = new ll[(n + 1)];
 90     g = MapManager(n, m << 1);
 91     vis = new boolean[(n + 1)];
 92     ll w;
 93     for (int i = 1, u, v; i <= m; i++) {
 94         scanf("%d%d"Auto, &u, &v, &w);
 95         g.addEdge(u, v, w);
 96         g.addEdge(v, u, w);
 97     }
 98 } 
 99 
100 void dfs(int p) {
101     vis[p] = true;
102     for (int i = g.h[p]; i; i = g[i].next) {
103         int e = g[i].end;
104         if (vis[e])
105             lb.insert(xs[e] ^ xs[p] ^ g[i].w);
106         else {
107             xs[e] = xs[p] ^ g[i].w;
108             dfs(e);
109         }
110     }
111 }
112 
113 inline void solve() {
114     memset(vis, false, sizeof(boolean) * (n + 1));
115     xs[1] = 0;
116     dfs(1);
117     printf(Auto"\n", lb.getAns(xs[n]));
118 }
119 
120 int main() {
121     init();
122     solve();
123     return 0;
124 }
posted @ 2018-03-03 20:31  阿波罗2003  阅读(141)  评论(0)  编辑  收藏  举报