NOI 2007 货币兑换Cash （bzoj 1492） - 斜率优化 - 动态规划 - CDQ分治

Description

小Y最近在一家金券交易所工作。该金券交易所只发行交易两种金券：A纪念券（以下简称A券）和 B纪念券（以下
简称B券）。每个持有金券的顾客都有一个自己的帐户。金券的数目可以是一个实数。每天随着市场的起伏波动，
两种金券都有自己当时的价值，即每一单位金券当天可以兑换的人民币数目。我们记录第 K 天中 A券 和 B券 的
价值分别为 AK 和 BK（元/单位金券）。为了方便顾客，金券交易所提供了一种非常方便的交易方式：比例交易法
。比例交易法分为两个方面：（a）卖出金券：顾客提供一个 [0,100] 内的实数 OP 作为卖出比例，其意义为：将
 OP% 的 A券和 OP% 的 B券 以当时的价值兑换为人民币；（b）买入金券：顾客支付 IP 元人民币，交易所将会兑
换给用户总价值为 IP 的金券，并且，满足提供给顾客的A券和B券的比例在第 K 天恰好为 RateK；例如，假定接
下来 3 天内的 Ak、Bk、RateK 的变化分别为：
假定在第一天时，用户手中有 100元 人民币但是没有任何金券。用户可以执行以下的操作：
注意到，同一天内可以进行多次操作。小Y是一个很有经济头脑的员工，通过较长时间的运作和行情测算，他已经
知道了未来N天内的A券和B券的价值以及Rate。他还希望能够计算出来，如果开始时拥有S元钱，那么N天后最多能
够获得多少元钱。

 

Input

输入第一行两个正整数N、S，分别表示小Y能预知的天数以及初始时拥有的钱数。接下来N行，第K行三个实数AK、B
K、RateK，意义如题目中所述。对于100%的测试数据，满足：0<AK≤10；0<BK≤10；0<RateK≤100；MaxProfit≤1
0^9。
【提示】
1.输入文件可能很大，请采用快速的读入方式。
2.必然存在一种最优的买卖方案满足：
每次买进操作使用完所有的人民币；
每次卖出操作卖出所有的金券。
 

Output

只有一个实数MaxProfit，表示第N天的操作结束时能够获得的最大的金钱数目。答案保留3位小数。

Sample Input

3 100
1 1 1
1 2 2
2 2 3

Sample Output

225.000

HINT

 

题目大意 每天可以根据一定比例购买或者卖出纪念劵。问最多在$n$天后可以得到多少钱。

 　　由题意易得，一定存在一种最优的方案满足，能买时就全买，能卖时就全卖。因为如果要赚就要尽可能地多赚，会亏就一点都不去碰。

 　　设$f[i]$表示第$i$天后把手上的纪念劵都卖掉后可以得到最多的钱，于是轻松地列出了dp方程：

$f[i] = \max\left \{ \frac{f[j]\left ( r_{j}A_{i} + B_{i} \right )}{r_{j}A_{j} + B_{j}}, f[i - 1] \right \}$

　　暂时先不管$\max$，当成等式，两边同除以$B_{i}$。

$\frac{f[i] }{B_{i}}= \frac{f[j]\left ( r_{j}\frac{A_{i}}{B_{i}} + 1 \right )}{r_{j}A_{j} + B_{j}}$

　　然后移移项什么的。。

$\frac{f[i] }{B_{i}}= \frac{f[j]r_{j}}{r_{j}A_{j} + B_{j}}\cdot \frac{A_{i}}{B_{i}}+\frac{ f[j]}{r_{j}A_{j} + B_{j}}$

$\frac{ f[j]}{r_{j}A_{j} + B_{j}}=- \frac{f[j]r_{j}}{r_{j}A_{j} + B_{j}}\cdot \frac{A_{i}}{B_{i}}+\frac{f[i] }{B_{i}}$

　　（第二步是把和$j$相关的扔到等号左边去，当做$y$，把形如$M\left(i\right)N\left(j \right )$，扔到左边，把其中的$M\left(i\right)$看作常数项，把$N\left(j \right )$看作$x$）

　　所以有：

$x_{i} = \frac{r_{i}f[i]}{r_{i}A_{i} + B{i}},y_{i}=\frac{f[i]}{r_{i}A_{i} + B{i}}$

　　然后可得：

$y_{j} = -\frac{A_{i}}{B_{i}}x_{j} + \frac{f[i]}{B_{i}}$

　　因为要最大化$f[i]$，所以应该最大化截距。所以维护上凸壳。

　　同时方程也可以写成：

$f[i] =\max\left \{ A_{i}x_{j}+B_{i}y_{j}, f[i - 1] \right \}$

　　考虑如何来求最大的截距。

　　因为这里插入点的$x$坐标不单调，询问的斜率也不单调，所以不能开单调队列暴力移指针了。

Solution 1 平衡树维护动态凸壳

　　（这是什么啊？可以吃吗？）

　　最后维护的凸壳是要长这个样子:

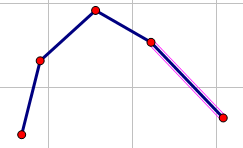
　　由于边不是很稳定，因为插入或者删除一个点，维护边的信息很麻烦。。。所以考虑用平衡树维护点，如果能够找到前驱后继，那么就可以轻松地找到边的信息。

　　由于要能找到边的信息，所以将点按照横坐标进行排序。

　　为了更好地偷懒，所以假设第0个点连接第1个点的直线的斜率为$inf$，最后一条点的后一条直线斜率为$-inf$

　　考虑插入一个点。

　　向左向右分别找到第一个能与它组成凸壳的点（即满足斜率递减，对于它前面的点来说就是，满足连接点$pre$的前驱和$pre$的直线的斜率大于连接点$pre$和当前点的直线的斜率）

　　显然这个东西可以二分。其实是不用的。。。（时间复杂均摊有保证，每个点被访后要么成为了要的点，结束了操作，要么被删了，所以时间复杂度$O\left(n\right)$）

　　当然还需要判断一下，这种情况

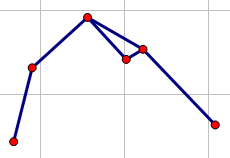
　　这种的话，只需要看看前面的点和后面的点以及当前点是否合法，不合法就说明当前点不该加入，否则就把它加入凸包。

　　至于如何维护前驱后继？

　　其实很简单，因为只在插入和删除的时候会发生改变，就在那个时候维护一下就好了。

　　现在考虑要在凸壳上找一个点，使得一条斜率为$k$的直线经过它，并且截距最大。

　　（这玩意儿显然可以三分）

　　

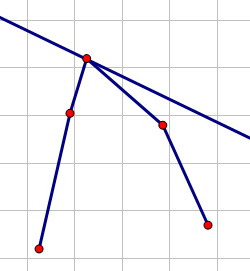
　　显然，当直线于凸壳相切（或者和凸壳的某一条边重合）的时候截距最大。不如一个不相切的情况：

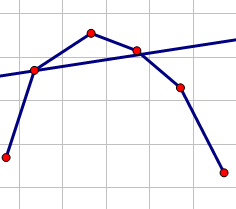
　　显然可以通过平移使得它更优。

　　考虑什么时候相切呢？当经过的点的前一条直线的斜率大于等于$k$，以及它的后一条直线的斜率小于等于$k$时。

　　这个显然可以二分。于是剩下的就是代码的问题。。

　　（注意精度问题。。）

Code

  1 /**
  2  * bzoj
  3  * Problem#1492
  4  * Accepted
  5  * Time: 1160ms
  6  * Memory: 11468k 
  7  */ 
  8 #include <bits/stdc++.h>
  9 using namespace std;
 10 typedef bool boolean;
 11 #define pnn pair<TreapNode*, TreapNode*>
 12 #define fi first
 13 #define sc second
 14 
 15 const double eps = 1e-7;
 16 
 17 int dcmp(double x) {
 18     if(fabs(x) < eps)    return 0;
 19     return (x > 0) ? (1) : (-1);
 20 }
 21 
 22 typedef class TreapNode {
 23     public:
 24         double x;
 25         double y;
 26         int rd;
 27         TreapNode *l, *r;
 28         TreapNode *pre, *suf;
 29 }TreapNode;
 30 
 31 #define Limit 200000
 32 
 33 TreapNode pool[Limit];
 34 TreapNode *top = pool;
 35 
 36 TreapNode* newnode(double x, double y) {
 37     top->x = x, top->y = y;
 38     top->l = top->r = NULL;
 39     top->rd = rand();
 40     return top++;
 41 }
 42 
 43 typedef class DynamicConvexHull {
 44     public:
 45         TreapNode* root;
 46         
 47         DynamicConvexHull():root(NULL) {        } 
 48         
 49         pnn split(TreapNode* p, double x) {
 50             if(!p)    return pnn(NULL, NULL);
 51             pnn rt;
 52             if(p->x - eps > x) {
 53                 rt = split(p->l, x);
 54                 p->l = rt.sc, rt.sc = p;
 55             } else {
 56                 rt = split(p->r, x);
 57                 p->r = rt.fi, rt.fi = p;
 58             }
 59             return rt;
 60         }
 61         
 62         TreapNode* merge(TreapNode* a, TreapNode* b) {
 63             if(a == NULL)    return b;
 64             if(b == NULL)    return a;
 65             if(a->rd > b->rd) {
 66                 a->r = merge(a->r, b);
 67                 return a;
 68             }
 69             b->l = merge(a, b->l);
 70             return b;
 71         }
 72         
 73         double slope(TreapNode* a, TreapNode* b) {
 74             if(a == NULL)    return 1e100;
 75             if(b == NULL)    return -1e100;
 76             if(!dcmp(a->x - b->x))
 77                 return (dcmp(a->y - b->y) == -1) ? (1e100) : (-1e100);
 78             return (a->y - b->y) / (a->x - b->x);
 79         }
 80 
 81         TreapNode* findPre(TreapNode* p, TreapNode* np) {
 82             TreapNode* rt = NULL;
 83             while(p) {
 84                 if(slope(p->pre, p) - eps > slope(p, np))
 85                     rt = p, p = p->r;
 86                 else
 87                     p = p->l;
 88             }
 89             return rt;
 90         }
 91 
 92         TreapNode* findSuf(TreapNode* p, TreapNode* np) {
 93             TreapNode* rt = NULL;
 94             while(p) {
 95                 if(slope(np, p) - eps > slope(p, p->suf))
 96                     rt = p, p = p->l;
 97                 else
 98                     p = p->r;    
 99             }
100             return rt;
101         }
102 
103         void insert(double x, double y) {
104             TreapNode* pn = newnode(x, y);
105             pnn pr = split(root, x);
106             TreapNode* pre = findPre(pr.fi, pn);
107             TreapNode* suf = findSuf(pr.sc, pn);
108             pn->pre = pre, pn->suf = suf;
109             if(slope(pre, pn) - eps >= slope(pn, suf)) {
110                 pr.fi = (pre) ? (split(pr.fi, pre->x + eps + eps).fi) : (NULL);
111                 pr.sc = (suf) ? (split(pr.sc, suf->x - eps - eps).sc) : (NULL);
112                 if(pre)    pre->suf = pn;
113                 if(suf)    suf->pre = pn;
114                 pr.fi = merge(pr.fi, pn);
115             }
116             root = merge(pr.fi, pr.sc);
117         }
118         
119         TreapNode* query(double k) {
120             TreapNode* p = root, *rt = NULL;
121             double cur, cmp;
122             while(p) {
123                 cur = slope(p->pre, p);
124                 if(cur - eps >= k) {
125                     if(!rt || cur + eps < cmp)
126                         rt = p, cmp = cur;
127                     p = p->r;
128                 } else
129                     p = p->l;
130             }
131             return rt;
132         }
133         
134 //        void debugOut(TreapNode* p) {
135 //            if(!p)    return;
136 //            debugOut(p->l);
137 //            cerr << "(" << p->x << ", " << p->y << ")" << endl;
138 //            debugOut(p->r);
139 //        }
140 }DynamicConvexHull;
141 
142 int n;
143 double *A, *B, *rate;
144 double *f;
145 DynamicConvexHull dch;
146 
147 inline void init() {
148     scanf("%d", &n);
149     A = new double[(n + 1)];
150     B = new double[(n + 1)];
151     f = new double[(n + 1)];
152     rate = new double[(n + 1)];
153     fill(f, f + n + 1, 0.0);
154     scanf("%lf", f);
155     for(int i = 1; i <= n; i++)
156         scanf("%lf%lf%lf", A + i, B + i, rate + i);
157 }
158 
159 inline void solve() {
160     f[1] = f[0];
161     double y = f[1] / (rate[1] * A[1] + B[1]);
162     double x = rate[1] * y, k;
163     dch.insert(x, y);
164     for(int i = 2; i <= n; i++) {
165         k = -A[i] / B[i];
166         TreapNode* rt = dch.query(k);
167         f[i] = A[i] * rt->x + B[i] * rt->y;
168         f[i] = max(f[i], f[i - 1]);
169         y = f[i] / (rate[i] * A[i] + B[i]);
170         x = y * rate[i];
171         dch.insert(x, y);
172     }
173     printf("%.3lf\n", f[n]);
174 }
175 
176 int main() {
177     init();
178     solve();
179     return 0;
180 }
Cash（平衡树维护动态凸壳）

Solution 2 CDQ分治

　　考虑当前要求出$[l, r]$中的dp值。

　　根据CDQ分治的常用套路，考虑左区间对右区间的贡献。

　　假设现在已经成功计算出左区间中的dp值，并将这些状态按照横坐标排序。

　　那么就可以用单调队列维护静态凸壳把左区间的凸壳建出来。

　　将右区间按照询问的斜率从大到小排序。

　　于是，这就变成了最智障的斜率优化问题了。。

　　但是$O\left ( n\log^{2}n \right )$会不会T掉？

　　考虑计算右区间的时候并不需要按照横坐标排序，而是按照询问的斜率排序。

　　所以，在分治前按照询问的斜率排序，然后在回溯的过程中按照横坐标进行归并。

　　于是成功去掉一个$\log$，总时间复杂度$O\left ( n\log n \right )$

　　但是因为自带大常数，比别人的Splay慢好多，sad....

Code

  1 /**
  2  * bzoj
  3  * Problem#1492
  4  * Accepted
  5  * Time: 1208ms
  6  * Memory: 8732k
  7  */ 
  8 #include <bits/stdc++.h>
  9 using namespace std;
 10 typedef bool boolean;
 11 
 12 const double eps = 1e-7;
 13 
 14 int dcmp(double x) {
 15     if(fabs(x) < eps)    return 0;
 16     return (x > 0) ? (1) : (-1);
 17 }
 18 
 19 typedef class Query {
 20     public:
 21         double k;
 22         int id;
 23         
 24         boolean operator < (Query b) const {
 25             return k > b.k;
 26         }
 27 }Query;
 28 
 29 int n;
 30 double *A, *B, *rate;
 31 double *xs, *ys;
 32 double *f;
 33 Query *qs, *qbuf;
 34 int* sta;
 35 
 36 inline void init() {
 37     scanf("%d", &n);
 38     A = new double[(n + 1)];
 39     B = new double[(n + 1)];
 40     rate = new double[(n + 1)];
 41     xs = new double[(n + 1)];
 42     ys = new double[(n + 1)];
 43     f = new double[(n + 1)];
 44     qs = new Query[(n + 1)];
 45     qbuf = new Query[(n + 1)];
 46     sta = new int[(n + 1)];
 47     scanf("%lf", f);
 48     for(int i = 1; i <= n; i++) {
 49         scanf("%lf%lf%lf", A + i, B + i, rate + i);
 50         qs[i].k = -A[i] / B[i], qs[i].id = i;
 51     }
 52 }
 53 
 54 double slope(int s, int t) {
 55     if(dcmp(xs[s] - xs[t]) == 0)    return (1e100);
 56     return (ys[t] - ys[s]) / (xs[t] - xs[s]); 
 57 }
 58 
 59 boolean cmpPoint(int a, int b) {
 60     int d = dcmp(xs[a] - xs[b]);
 61     return (d == -1 || (d == 0 && dcmp(ys[a] - ys[b]) == -1));
 62 }
 63 
 64 void CDQDividing(int l, int r, int L, int R) {
 65     if(l == r) {
 66         f[l] = max(f[l], f[l - 1]);
 67         xs[l] = rate[l] * f[l] / (rate[l] * A[l] + B[l]);
 68         ys[l] = f[l] / (rate[l] * A[l] + B[l]);
 69         return; 
 70     }
 71     
 72     int mid = (l + r) >> 1, qL = L - 1, qR = mid;
 73     
 74     for(int i = L; i <= R; i++)
 75         if(qs[i].id <= mid)
 76             qbuf[++qL] = qs[i];
 77         else
 78             qbuf[++qR] = qs[i];
 79     for(int i = L; i <= qR; i++)
 80         qs[i] = qbuf[i];
 81     CDQDividing(l, mid, L, qL);
 82     
 83     int pl = 1, pr = 0, t = L;
 84     for(int i = L; i <= qL; i++) {
 85         while(pr - pl > 0 && dcmp(slope(sta[pr - 1], sta[pr]) - slope(sta[pr], qs[i].id)) != 1)    pr--;
 86         sta[++pr] = qs[i].id;
 87     }
 88     
 89     for(int i = mid + 1, id; i <= R; i++) {
 90         id = qs[i].id;
 91         while(pr - pl > 0 && dcmp(qs[i].k - slope(sta[pl], sta[pl + 1])) == -1)    pl++;
 92         f[id] = max(f[id], A[id] * xs[sta[pl]] + B[id] * ys[sta[pl]]);
 93     }
 94     
 95     CDQDividing(mid + 1, r, mid + 1, R);
 96     
 97     pl = L, pr = mid + 1;
 98     while(pl <= qL || pr <= R) {
 99         if((pr > R) || (pl <= qL && cmpPoint(qs[pl].id, qs[pr].id)))
100             qbuf[t++] = qs[pl++];
101         else
102             qbuf[t++] = qs[pr++];
103     }
104     for(int i = L; i <= R; i++)
105         qs[i] = qbuf[i];
106 }
107 
108 inline void solve() {
109     sort(qs + 1, qs + n + 1);
110     fill(f + 1, f + n + 1, 0);
111     CDQDividing(1, n, 1, n);
112     printf("%.3lf\n", f[n]);
113 }
114 
115 int main() {
116     init();
117     solve();
118     return 0;
119 }
posted @ 2018-01-07 13:26  阿波罗2003  阅读(275)  评论(0)  编辑  收藏  举报