bzoj 4008 亚瑟王 - 动态规划 - 概率与期望

Description

小 K 不慎被 LL 邪教洗脑了，洗脑程度深到他甚至想要从亚瑟王邪教中脱坑。

他决定，在脱坑之前，最后再来打一盘亚瑟王。既然是最后一战，就一定要打得漂

亮。众所周知，亚瑟王是一个看脸的游戏，技能的发动都是看概率的。作为一个非

洲人，同时作为一个前 OIer，小 K 自然是希望最大化造成伤害的期望值。但他已

经多年没写过代码，连 Spaly都敲不对了，因此，希望你能帮帮小 K，让他感受一

下当欧洲人是怎样的体验。 

本题中我们将考虑游戏的一个简化版模型。 

玩家有一套卡牌，共 n张。游戏时，玩家将 n 张卡牌排列成某种顺序，排列后

将卡牌按从前往后依次编号为 1 ~  n。本题中，顺序已经确定，即为输入的顺序。

每张卡牌都有一个技能。第 i 张卡牌的技能发动概率为 pi，如果成功发动，则会对

敌方造成di点伤害。也只有通过发动技能，卡牌才能对敌方造成伤害。基于现实因

素以及小K非洲血统的考虑，pi不会为 0，也不会为 1，即 0 < pi < 1。 

一局游戏一共有 r 轮。在每一轮中，系统将从第一张卡牌开始，按照顺序依次

考虑每张卡牌。在一轮中，对于依次考虑的每一张卡牌： 

1如果这张卡牌在这一局游戏中已经发动过技能，则 

1.1 如果这张卡牌不是最后一张，则跳过之（考虑下一张卡牌）； 

否则（是最后一张），结束这一轮游戏。 

2否则（这张卡牌在这一局游戏中没有发动过技能），设这张卡牌为第 i 张 

2.1将其以 pi的概率发动技能。 

2.2如果技能发动，则对敌方造成 di点伤害，并结束这一轮。 

2.3如果这张卡牌已经是最后一张（即 i 等于n），则结束这一轮；否则，

考虑下一张卡牌。 

请帮助小 K 求出这一套卡牌在一局游戏中能造成的伤害的期望值。 

Input

输入文件的第一行包含一个整数 T，代表测试数据组数。 

接下来一共 T 组数据。 

每组数据的第一行包含两个用空格分开的整数 n和r，分别代表卡牌的张数和

游戏的轮数。 

接下来 n行，每行包含一个实数和一个整数，由空格隔开，描述一张卡牌。第

i 行的两个数为 pi和 di，分别代表第 i 张卡牌技能发动的概率（实数）和技能发动

造成的伤害（整数）。保证 pi最多包含 4位小数，且为一个合法的概率。 

Output

 对于每组数据，输出一行，包含一个实数，为这套卡牌在这一局游戏中造成的

伤害的期望值。对于每一行输出，只有当你的输出和标准答案的相对误差不超过

10^-8时——即|a-o|/a<=10-8时(其中a是标准答案，o是输出)，你的输出才会被判为正确。

建议输出10 位小数。 

Sample Input

1
3 2
0.5000 2
0.3000 3
0.9000 1

Sample Output

3.2660250000

HINT

 

 一共有 13 种可能的情况： 

1.  第一轮中，第 1张卡牌发动技能；第二轮中，第 2张卡牌发动技能； 

概率为 0.15，伤害为5。 

2.  第一轮中，第 1张卡牌发动技能；第二轮中，第 3张卡牌发动技能； 

概率为 0.315，伤害为3。 

3.  第一轮中，第 1张卡牌发动技能；第二轮不发动技能； 

概率为 0.035，伤害为2。 

4.  第一轮中，第 2张卡牌发动技能；第二轮中，第 1张卡牌发动技能； 

概率为 0.075，伤害为5。 

5.  第一轮中，第 2张卡牌发动技能；第二轮中，第 3张卡牌发动技能； 

概率为 0.0675，伤害为4。 

6.  第一轮中，第 2张卡牌发动技能；第二轮不发动技能； 

概率为 0.0075，伤害为3。 

7.  第一轮中，第 3张卡牌发动技能；第二轮中，第 1张卡牌发动技能； 

概率为 0.1575，伤害为3。 

8.  第一轮中，第 3张卡牌发动技能；第二轮中，第 2张卡牌发动技能； 

概率为 0.04725，伤害为4。 

9.  第一轮中，第 3张卡牌发动技能；第二轮不发动技能； 

概率为 0.11025，伤害为1。 

10.  第一轮不发动技能；第二轮中，第 1张卡牌发动技能； 

概率为 0.0175，伤害为2。 

11.  第一轮不发动技能；第二轮中，第 2张卡牌发动技能； 

概率为 0.00525，伤害为3。 

12.  第一轮不发动技能；第二轮中，第 3张卡牌发动技能； 

概率为 0.011025，伤害为1。 

13.  第一轮不发动技能；第二轮亦不发动技能； 

概率为 0.001225，伤害为0。 

造成伤害的期望值为概率与对应伤害乘积之和，为 3.266025。 

 

对于所有测试数据， 1 <= T <= 444， 1 <= n <= 220， 0 <= r <= 132， 0 < pi < 1， 0 <= di <= 1000。  

除非备注中有特殊说明，数据中 pi与di均为随机生成。 

请注意可能存在的实数精度问题，并采取适当措施。 

---

　　题目大意 有n张卡牌，进行r轮游戏，每一轮，从第1张卡牌开始考虑，第i张牌如果没有发动过，则有p[i]的概率对分数有d[i]的贡献，发动后立刻结束这轮游戏。问期望的分数。

　　有注意到每张卡牌发动的概率之和它之前的牌有关。

　　考虑用f[i][j]表示当第i张牌得到j次发动机会的概率。

　　根据dp的某些神奇的性质，只需要考虑第i张卡牌和第(i - 1)张卡牌就可以了(因为这样做的话，f[i - 1]包含了第(i - 2)张卡牌的相关信息，大概感觉有点像递归定义。。)

　　1.第(i - 1)张卡牌在j次机会中1次都没有发动

　　　　显然它的概率为。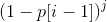

　　2.第(i - 1)张卡牌在(j + 1)次机会中发动了1次

　　　　可以求对立事件的概率，然后拿1去减它，于是得到了它的概率为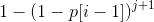

　　　　不能理解？那我们换个方法，考虑在第i次机会发动，然后求和:

　　　　然后用等比数列求和公式:

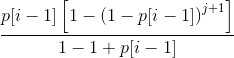
　　　　化简得到: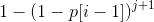

　　于是转移转移就好了。

Code

/**
 * bzoj
 * Problem#4008
 * Accepted
 * Time: 848ms
 * Memory: 1764k
 */
#include <bits/stdc++.h>
using namespace std;

const int N = 225, R = 135;

int T;
int n, r;
int W[N];
double P[N];
double prP[N][R];
double f[N][R];

inline void prepare() {
    for(int i = 0; i < N; i++)
        prP[i][0] = 1;
    for(int i = 1; i < R; i++)
        prP[0][i] = 1;
}

inline void init() {
    scanf("%d%d", &n, &r);
    for(int i = 1; i <= n; i++)
        scanf("%lf%d", P + i, W + i);
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= r; j++)
            prP[i][j] = prP[i][j - 1] * (1 - P[i]);//, cerr << prP[i][j] << endl;
}

inline void solve() {
    memset(f, 0, sizeof(f));
    f[0][r] = 1;
    double ans = 0.0;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= r; j++) {
            f[i][j] = f[i - 1][j] * prP[i - 1][j] + f[i - 1][j + 1] * (1 - prP[i - 1][j + 1]);
            ans += f[i][j] * (1 - prP[i][j]) * W[i];
        }
    printf("%.10lf\n", ans);
}

int main() {
    prepare();
    scanf("%d", &T);
    while(T--) {
        init();
        solve();
    }
    return 0;
}