bzoj 3489 A simple rmq problem - 线段树
Description
因为是OJ上的题,就简单点好了。给出一个长度为n的序列,给出M个询问:在[l,r]之间找到一个在这个区间里只出现过一次的数,并且要求找的这个数尽可能大。如果找不到这样的数,则直接输出0。我会采取一些措施强制在线。
Input
第一行为两个整数N,M。M是询问数,N是序列的长度(N<=100000,M<=200000)
第二行为N个整数,描述这个序列{ai},其中所有1<=ai<=N
再下面M行,每行两个整数x,y,
询问区间[l,r]由下列规则产生(OIER都知道是怎样的吧>_<):
l=min((x+lastans)mod n+1,(y+lastans)mod n+1);
r=max((x+lastans)mod n+1,(y+lastans)mod n+1);
Lastans表示上一个询问的答案,一开始lastans为0
Output
一共M行,每行给出每个询问的答案。
Sample Input
10 10
6 4 9 10 9 10 9 4 10 4
3 8
10 1
3 4
9 4
8 1
7 8
2 9
1 1
7 3
9 9
6 4 9 10 9 10 9 4 10 4
3 8
10 1
3 4
9 4
8 1
7 8
2 9
1 1
7 3
9 9
Sample Output
4
10
10
0
0
10
0
4
0
4
10
10
0
0
10
0
4
0
4
HINT
注意出题人为了方便,input的第二行最后多了个空格。
2015.6.24新加数据一组,2016.7.9放至40S,600M,但未重测
Source
题目大意 询问区间内只出现1次数的最大值。强制在线。
考虑每位置上的数会对哪些询问作出贡献。
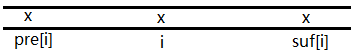
显然要让位置i对答案产生贡献询问的区间需要满足 pre[i] < l <= i 并且 i <= r < suf[i] 。
那么就可以将每个询问(l, r)看成二维平面内的一个点。
这样的话,每个位置对答案的贡献就可以通过2维线段树来进行维护。
为了防止MLE,所以采取标记永久化的方案。但是注意修改操作是和线段树维护的信息取max。
Code
1 /** 2 * bzoj 3 * Problem#3489 4 * Accepted 5 * Time: 21836ms 6 * Memory: 227780k 7 */ 8 #include <bits/stdc++.h> 9 using namespace std; 10 typedef bool boolean; 11 12 typedef class SegTreeNode { 13 public: 14 SegTreeNode* val; 15 SegTreeNode *l, *r; 16 17 SegTreeNode(int val = 0):val((SegTreeNode*)val) { } 18 SegTreeNode(int val, SegTreeNode* org):val((SegTreeNode*)val) { 19 l = r = org; 20 } 21 22 int intvalue() { 23 return (int)val; 24 } 25 26 SegTreeNode*& pnodeval() { 27 return val; 28 } 29 30 void set(int x) { 31 val = (SegTreeNode*)x; 32 } 33 }SegTreeNode; 34 35 #define PLimit 10000000 36 37 //int alloced = 0; 38 SegTreeNode pool[PLimit]; 39 SegTreeNode null = SegTreeNode(0, &null); 40 SegTreeNode* top = pool; 41 42 SegTreeNode* newnode() { 43 // alloced++; 44 if(top >= pool + PLimit) 45 return new SegTreeNode(0, &null); 46 *top = SegTreeNode(0, &null); 47 return top++; 48 } 49 50 typedef class SegTree { 51 public: 52 int n; 53 SegTreeNode* rt; 54 55 SegTree() { } 56 SegTree(int n):n(n), rt(newnode()) { } 57 58 void update2(SegTreeNode*& node, int l, int r, int ql, int qr, int val) { 59 if(node == &null || node == NULL) 60 node = newnode(); 61 if(l == ql && r == qr) { 62 if(val > node->intvalue()) 63 node->set(val); 64 return; 65 } 66 int mid = (l + r) >> 1; 67 if(ql <= mid) 68 update2(node->l, l, mid, ql, (qr > mid) ? (mid) : (qr), val); 69 if(qr > mid) 70 update2(node->r, mid + 1, r, (ql > mid) ? (ql) : (mid + 1), qr, val); 71 } 72 73 void update(SegTreeNode*& node, int l, int r, int ql, int qr, int qx, int qy, int val) { 74 if(node == &null) 75 node = newnode(); 76 if(l == ql && r == qr) { 77 update2(node->pnodeval(), 1, n, qx, qy, val); 78 return; 79 } 80 int mid = (l + r) >> 1; 81 if(ql <= mid) 82 update(node->l, l, mid, ql, (qr > mid) ? (mid) : (qr), qx, qy, val); 83 if(qr > mid) 84 update(node->r, mid + 1, r, (ql > mid) ? (ql) : (mid + 1), qr, qx, qy, val); 85 } 86 87 int query2(SegTreeNode*& node, int l, int r, int idx) { 88 if(node == NULL || node == &null) 89 return 0; 90 if(l == idx && r == idx) 91 return node->intvalue(); 92 int mid = (l + r) >> 1, rt = node->intvalue(), cmp = 0; 93 if(idx <= mid) 94 cmp = query2(node->l, l, mid, idx); 95 else 96 cmp = query2(node->r, mid + 1, r, idx); 97 return (cmp > rt) ? (cmp) : (rt); 98 } 99 100 int query(SegTreeNode*& node, int l, int r, int idx, int bidx) { 101 if(node == &null) 102 return 0; 103 if(l == idx && r == idx) 104 return query2(node->pnodeval(), 1, n, bidx); 105 int mid = (l + r) >> 1, rt = query2(node->pnodeval(), 1, n, bidx), cmp; 106 if(idx <= mid) 107 cmp = query(node->l, l, mid, idx, bidx); 108 else 109 cmp = query(node->r, mid + 1, r, idx, bidx); 110 return (cmp > rt) ? (cmp) : (rt); 111 } 112 }SegTree; 113 114 int n, m; 115 int *ar; 116 int *pre, *suf; 117 int *head; 118 SegTree st; 119 120 inline void init() { 121 scanf("%d%d", &n, &m); 122 st = SegTree(n); 123 ar = new int[(n + 1)]; 124 pre = new int[(n + 1)]; 125 suf = new int[(n + 1)]; 126 head = new int[(n + 1)]; 127 for(int i = 1; i <= n; i++) 128 scanf("%d", ar + i); 129 } 130 131 inline void solve() { 132 memset(head, 0, sizeof(int) * (n + 1)); 133 for(int i = 1; i <= n; i++) 134 pre[i] = head[ar[i]], head[ar[i]] = i; 135 fill(head, head + n + 1, n + 1); 136 for(int i = n; i; i--) 137 suf[i] = head[ar[i]], head[ar[i]] = i; 138 139 for(int i = 1; i <= n; i++) 140 st.update(st.rt, 1, n, pre[i] + 1, i, i, suf[i] - 1, ar[i]);//, fprintf(stderr, "%d: Memory Usage: %d (%d nodes)\n", i, alloced * sizeof(SegTreeNode), alloced); 141 int lastans = 0, x, y; 142 while(m--) { 143 scanf("%d%d", &x, &y); 144 x = (x + lastans) % n + 1; 145 y = (y + lastans) % n + 1; 146 if(x > y) swap(x, y); 147 lastans = st.query(st.rt, 1, n, x, y); 148 printf("%d\n", lastans); 149 } 150 } 151 152 int main() { 153 init(); 154 solve(); 155 return 0; 156 }

