bzoj 2873 光之大陆 - 动态规划 - 组合数学

Description

在光之大陆的土地上，各种势力盘根错节。来自光之峡谷的精灵，来自黑暗森林的亡灵，来自古老东方的人类共同生活在一起。善于打造装置的矮人，善于发明的侏儒，隐匿于山林的巨人也坚守着属于自己的领土。这些种族之间关系错综复杂，构成了极其庞大的关系网络。大魔法师小P想要研究其中的种族关系。

两个物种之间可以是盟友，也可以不是盟友，如果a1,a2..an满足ai和ai+1是盟友，且an和a1是盟友，则他们构成了一个联盟。

由于光之大陆正处于微妙的和平之中。所以一个合理的物种关系应满足如下条件:

1、对于任意两个物种A,B,都存在一个序列A,a1,a2..an,B,使得任意相邻两个种族是盟友(注意A,B不一定是盟友)。

2、对于任意两个联盟Sa,Sb,都不存在一个物种既参加了联盟Sa，又参加了联盟Sb。

小P想知道，大陆上的N个种族一共有多少种可能的结盟关系，由于结果可能很大，你只需要输出答案mod M的值。

 

Input

一行两个正整数：N,M（含义如题所述）

Output

一个整数：ans表示方案mod M的值

Sample Input

4 1000000

Sample Output

31

HINT

100%测试点保证 n <= 200, m <= 1000000

---

　　题目大意 问n个点，每个点最多属于1个环，组成的没有重边和自环连通图的个数(每个点互不相同)

　　用f[i]表示答案，g[i][j]表示，i个点分成j个满足条件的连通块，并且自带一个插口的方案数。(这个有何意义？等会儿就知道了)

　　先来讨论我们最关心的答案f[i]

　　考虑加入点i(这个点是有序的，不是随便抓个点出来都能叫点i)

　　　　1)如果点i不属于任何环，那简单，枚举分支个数，然后求个和就行了。即

　　　　2)如果点i属于一个环(因为没有重边和自环所以至少3个点才能组成)

　　　　　　i.如果不是所有点都拿来构成一个环，设环的大小为j

　　　　　　　　考虑抓另外k- 1个点形成一个环的方案数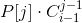(P[j]是什么鬼？是j个互不相同的点构成的不同的环的方案数，下面讲计算方式)。

　　　　　　　　然后考虑剩下(i - j)个点，枚举连通块的个数，然后再计算分别插在环上的方案总数(只能用插头去插)，即

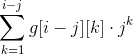
　　　　　　　　然后根据乘法原理得到:

 

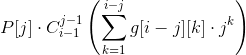
　　　　　　ii.考虑把所有点拿来构成一个环(其实初值设得好不用考虑这个东西)

　　　　　　　　这个比较简单P[i]加上，完事。

　　所以综上所述，我们有

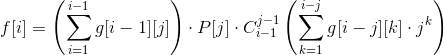
　　然后再来考虑g[i][j]，此时应该会轻松很多了。

　　初值g[0][0] = 1(其实我是先有式子再来推需要的初值)

　　考虑添加一个有k个点的满足条件的连通块(包含点i)，方案数为多少呢？

　　是不是f[k]啊？(算过的)

　　在考虑除开点i，剩下的点中选出k - 1个点与之为伴。

　　然后再从k个点中选出1个做插头。

　　所以轻松地得到下面这个式子

　　

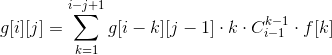
　　注意要预处理i的k次幂不然每次快速幂很慢。另外，组合数最好用杨辉恒等式预处理一下，主要原因是逆元可能不存在，其次原因是否则每次用组合数会比较慢。

　　上面提到的P[i]现在来讲推理方法(一个简单易懂的方法)。

　　首先我们选定点1，从它那将环剖开，然后剩下的数随便排在它后面，故有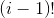个方案，但是形成环以后，从1开始的正反此序会导致重复1次，例如1 3 2和1 2 3。所以还需要除以2,。所以我们得到:

　　

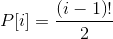
Code

/**
 * bzoj
 * Problem#2873
 * Accepted
 * Time: 788ms
 * Memory: 1788K
 */ 
#include <bits/stdc++.h>
using namespace std;
#define ll long long

const int N = 205;

int n, m;

inline void init() {
    scanf("%d%d", &n, &m);
}

int f[N];
int g[N][N];
int C[N][N];
int power[N][N];
int P[N];
inline void solve() {
    P[0] = P[1] = P[2] = 0;
    P[3] = 1;
    for(int i = 4; i <= n; i++)
        P[i] = P[i - 1] * (i - 1) % m;
    
    C[0][0] = 1 % m;
    for(int i = 1; i <= n; i++) {
        C[i][0] = C[i][i] = 1 % m;
        for(int j = 1; j < i; j++)
            C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % m;
    }
    
    for(int i = 1; i <= n; i++) {
        power[i][0] = 1 % m;
        for(int j = 1; j <= n; j++)
            power[i][j] = power[i][j - 1] * i % m;
    }
    
    f[1] = f[2] = 1 % m;
    g[0][0] = g[1][1] = 1 % m, g[2][1] = 2 % m, g[2][2] = 1 % m;
    for(int i = 3; i <= n; i++) {
        for(int j = 1; j < i; j++)
            f[i] = (f[i] + g[i - 1][j]) % m;
        
        for(int j = 3; j < i; j++) {
            int temp = 0;
            for(int k = 1; k <= i - j; k++)
                temp = (temp + g[i - j][k] * 1ll * power[j][k]) % m;
            f[i] = (f[i] + ((P[j] * 1ll * C[i - 1][j - 1]) % m * temp) % m) % m;
        }
        
        f[i] = (f[i] + P[i]) % m;
        
        for(int j = 1; j <= i; j++) {
            for(int k = 1; k <= i - j + 1; k++)
                g[i][j] = (g[i][j] + (((g[i - k][j - 1] * 1ll * k % m) * f[k] % m) * C[i - 1][k - 1]) % m) % m;
//            printf("g[%d][%d]:%d\n", i, j, g[i][j]);
        }
    }
    printf("%d", f[n]);
}

int main() {
    init();
    solve();
    return 0;
}