Codeforces 526F Pudding Monsters - CDQ分治 - 桶排序

In this problem you will meet the simplified model of game Pudding Monsters.

An important process in developing any game is creating levels. A game field in Pudding Monsters is an n × n rectangular grid, n of its cells contain monsters and some other cells contain game objects. The gameplay is about moving the monsters around the field. When two monsters are touching each other, they glue together into a single big one (as they are from pudding, remember?).

Statistics showed that the most interesting maps appear if initially each row and each column contains exactly one monster and the rest of map specifics is set up by the correct positioning of the other game objects.

A technique that's widely used to make the development process more efficient is reusing the available resources. For example, if there is a large n × n map, you can choose in it a smaller k × k square part, containing exactly k monsters and suggest it as a simplified version of the original map.

You wonder how many ways there are to choose in the initial map a k × k (1 ≤ k ≤ n) square fragment, containing exactly k pudding monsters. Calculate this number.

Input

The first line contains a single integer n (1 ≤ n ≤ 3 × 105) — the size of the initial field.

Next n lines contain the coordinates of the cells initially containing monsters. The i-th of the next lines contains two numbers ri, ci(1 ≤ ri, ci ≤ n) — the row number and the column number of the cell that initially contains the i-th monster.

It is guaranteed that all ri are distinct numbers and all ci are distinct numbers.

Output

Print the number of distinct square fragments of the original field that can form a new map.

Examples

input

5
1 1
4 3
3 2
2 4
5 5

output

10

---

　　题目大意 给定平面上有n个点，每行每列上只有一个点，问总共有多少个边长为k的矩形框住了k个点。

　　刚开学，好久(也就两周)都没搞OI，差点不知OI为何物了。qaq。有人把这道题改题面拿给我们考试，然后考试时没想出正解，暴力分段90分。。于是班上出现了一群优秀的魔(膜)法师。

　　显然，可以把它转化成序列上的问题(序列就是a[i]表示第i列上的点的纵坐标):有多少个长度为k的区间使得这一段的最大值和最小值之差等于k - 1。

　　然后上CDQ分治进行瞎搞。记当前分治区间为[l, r]，分治中心为mid，统计经过分治中心的子区间，分四种情况讨论:

　　1)子区间的最大值和最小值同在左侧(相对于分治中心)

　　2)子区间的最小值在左侧，最大值在右侧

　　3)子区间的最大值和最小值同在右侧

　　4)子区间的最大值在左侧，最小值在右侧

　　由于情况1,3和2,4的做法类似，所以只考虑情况1,2

　　情况1:

　　　　记录左侧每个位置到分治中心的最大值和最小值。

　　　　枚举子区间的左端点，可以根据记录的数据计算出右端点，如果合法(在分治中心右侧，并且最大值和最小值满足在左侧)就将答案加1.

　　情况2:

　　　　从分治中心向左枚举左端点i，考虑先使最值的条件合法。

　　　　考虑到前后缀最大值和最小值都有不增或不减的单调性。所以设置两个"指针",r1和r2。

　　　　r1是第一个使最大值在右侧的位置，r2是第一个使最小值不在左边的位置。那么左端点为i，右端点在整数区间[r1, r2)内的子区间都满足最值的限制。

　　　　现在考虑如何统计答案。临时约定max[l, r]表示a[l]，a[l + 1], ..., a[r]的最大值，同理定义min[l, r]。

　　　　显然

　　　　移一下项得到

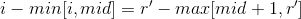
　　　　所以在挪动"指针"的时候把右边的一坨东东扔进某个桶里面就好了。挪动完成后根据当前枚举的左端点i，首先判断是否合法(比如什么r1大于等于r2的时候就continue就好了，如果合法的话就加上对应桶里的计数就好了。

　　　　这种情况搞定了之后，不要忘记清空桶，由于桶可能很大，所以不要memset或者fill，for数组a就好了。

Code

/**
 * Codeforces
 * Problem#526F
 * Accepted
 * Time: 140ms
 * Memory: 8200k
 */
#include <iostream>
#include <fstream>
#include <sstream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <ctime>
#include <cctype>
#include <algorithm>
#include <set>
#include <map>
#include <vector>
#include <queue>
#include <stack>
#include <bitset>
#ifndef WIN32
#define Auto "%lld"
#else
#define Auto "%I64d"
#endif
using namespace std;
typedef bool boolean;
#define clra(a) memset(a, false, sizeof(a))
const signed int inf = ((~0u) >> 1);
#define smin(a, b) a = min(a, b)
#define smax(a, b) a = max(a, b)
#define LL long long

const int N = 3e5;

int n;
int *arr;
int *pmin, *pmax, *rmin, *rmax;
int bucket[(N << 1) + 5];

inline void init() {
    scanf("%d", &n);
    arr = new int[(n + 1)];
    pmin = new int[(n + 1)];
    pmax = new int[(n + 1)];
    rmin = new int[(n + 1)];
    rmax = new int[(n + 1)];
    for(int i = 1, x, y; i <= n; i++) {
        scanf("%d%d", &x, &y);
        arr[x] = y;
    }
}

LL CDQDividing(int l, int r) {
    if(l == r)    return 1;
    
    int mid = (l + r) >> 1;
    LL rt = 0;
    pmin[mid] = arr[mid], pmax[mid] = arr[mid], rmin[mid + 1] = arr[mid + 1], rmax[mid + 1] = arr[mid + 1];
    for(int i = mid - 1; i >= l; i--)
        pmin[i] = min(pmin[i + 1], arr[i]), pmax[i] = max(pmax[i + 1], arr[i]);
    for(int i = mid + 2; i <= r; i++)
        rmin[i] = min(rmin[i - 1], arr[i]), rmax[i] = max(rmax[i - 1], arr[i]);
        
    for(int i = l, rg; i <= mid; i++) {
        rg = i + pmax[i] - pmin[i];
        rt += rg > mid && rg <= r && rmax[rg] < pmax[i] && rmin[rg] > pmin[i];
    }
    for(int i = mid + 1, lf; i <= r; i++) {
        lf = i - rmax[i] + rmin[i];
        rt += lf <= mid && lf >= l && pmax[lf] < rmax[i] && pmin[lf] > rmin[i];
    }
    for(int i = mid, r1 = mid + 1, r2 = mid + 1; i >= l && r1 <= r; i--) {    // The min num is on the left.
        while(r2 <= r && rmin[r2] > pmin[i])    bucket[r2 - rmax[r2] + N]++, r2++;
        while(r1 <= r && rmax[r1] < pmax[i])    bucket[r1 - rmax[r1] + N]--, r1++;
        if(r1 < r2)    rt += bucket[i - pmin[i] + N];
    }
    for(int i = mid + 1; i <= r; i++)
        bucket[i - rmax[i] + N] = 0;
//    cout << rt << endl;
    for(int i = mid + 1, l1 = mid, l2 = mid; i <= r && l2 >= l; i++) {    // The min num is on the right.
        while(l1 >= l && pmin[l1] > rmin[i])    bucket[l1 + pmax[l1]]++, l1--;
        while(l2 >= l && pmax[l2] < rmax[i])    bucket[l2 + pmax[l2]]--, l2--;
        if(l1 < l2)    rt += bucket[i + rmin[i]];
    }
    for(int i = l; i <= mid; i++)
        bucket[i + pmax[i]] = 0;
    
    return rt + CDQDividing(l, mid) + CDQDividing(mid + 1, r);
}

inline void solve() {
    printf(Auto, CDQDividing(1, n));
}

int main() {
    init();
    solve();
    return 0;
}