bzoj 3560 DZY Loves Math V - 线性筛 - 扩展欧几里得算法
给定n个正整数a1,a2,…,an,求
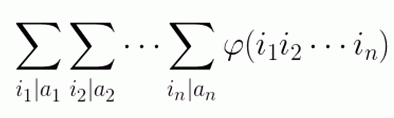
的值(答案模10^9+7)。
Input
Output
仅一行答案。
Sample Input
3 6 10 15
Sample Output
1595
Hint
1<=n<=10^5,1<=ai<=10^7。共3组数据。
题目大意 (题目过于简洁,完全不需要大意)
题目虽然很简洁,但是处处挖着坑等你跳。
原计划两个小时把今天讲的例题A完,实际上两个小时都被这道题坑走了(懒惰于重新推公式的下场。。。)
//假设读者知道什么是积性函数以及欧拉函数的积性
欧拉函数的积性可以表现在这种形式(里面p + 下标都表示互不相同的质数):
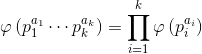
所以,我们可以把每个不同的素数分开进行计算贡献,然后再求积(因为我们是把每个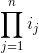 像上述形式拆分求phi值,所以是求积)。
像上述形式拆分求phi值,所以是求积)。
于是我们成功得到了某个更长的式子:(其中b(p)i表示ai中质因子p的指数)

由于欧拉函数在此不好运用某些套路快速求结果,所以考虑运用欧拉函数神奇的性质将其拆开。我们知道有关欧拉函数有(同样,p是质数)
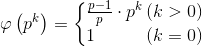
虽然当指数为0的时候为特殊情况,但是可以加点黑科技是它不是那么地特殊:
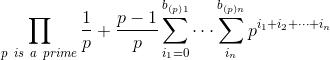
是滴,多加了一个1/p就解决了问题。现在继续化简:
$\prod_{p\ is\ a\ prime}\frac{1}{p} + \frac{p - 1}{p}\left ( \sum_{i_{1} = 0}^{b_{\left ( p \right )1}}p^{i_{1}} \right )\cdots \left( \sum_{i_{n} = 0}^{b_{\left ( p \right )n}}p^{i_{n}} \right )$
然后得到了:
$\prod_{p\ is\ a\ prime}\frac{1 + \left (p - 1 \right )\left ( \sum_{i_{1} = 0}^{b_{\left ( p \right )1}}p^{i_{1}} \right )\cdots \left( \sum_{i_{n} = 0}^{b_{\left ( p \right )n}}p^{i_{n}} \right )}{p}$
此时计算的时间复杂度能够接受。但是由于在模意义下做除法需要乘逆元,由于p是小于1e7的质数,所以一定和1e9 + 7互质,所以逆元一定存在。
关于这道题还有很神奇的东西,存有哪些不同的素数用STL(Standard Templates Library Sometimes/Standard TLE/MLE Library),然而MLE。。。求解释。。。好像和理论算的不太一样。。
所以就用一个黑科技。用pair的第一位存是什么素数,第二位存指数。然后sort一下,就可以AC了。
Code
1 /** 2 * bzoj 3 * Problem#3560 4 * Accepted 5 * Time: 1276ms 6 * Memory: 7940k 7 */ 8 #include <bits/stdc++.h> 9 #ifndef WIN32 10 #define Auto "%lld" 11 #else 12 #define Auto "%I64d" 13 #endif 14 using namespace std; 15 typedef bool boolean; 16 #define smax(a, b) a = max(a, b) 17 #define LL long long 18 19 const int moder = 1e9 + 7; 20 LL mpow(LL a, LL pos) { 21 if(pos == 0) return 1; 22 if(pos == 1) return a; 23 LL temp = mpow(a, pos >> 1); 24 temp = (temp * temp) % moder; 25 if(pos & 1) temp = (temp * a) % moder; 26 return temp; 27 } 28 29 void exgcd(LL a, LL b, LL& d, LL& x, LL& y) { 30 if(!b) { 31 d = a; 32 x = 1, y = 0; 33 } else { 34 exgcd(b, a % b, d, y, x); 35 y -= (a / b) * x; 36 } 37 } 38 39 int inv(int a, int moder) { 40 LL d, x, y; 41 exgcd(a, moder, d, x, y); 42 return (x < 0) ? (x + moder) : (x); 43 } 44 45 const int limit = 3500; 46 int num = 0; 47 int prime[1000]; 48 boolean vis[limit + 1]; 49 inline void Euler() { 50 for(int i = 2; i <= limit; i++) { 51 if(!vis[i]) prime[num++] = i; 52 for(int j = 0; j < num && i * prime[j] <= limit; j++) { 53 vis[i * prime[j]] = true; 54 if((i % prime[j] == 0)) 55 break; 56 } 57 } 58 } 59 60 int n; 61 int* arr; 62 int cnt = 0; 63 pair<int, int> ds[800005]; 64 inline void init() { 65 scanf("%d", &n); 66 arr = new int[(n + 1)]; 67 for(int i = 1; i <= n; i++) { 68 scanf("%d", arr + i); 69 } 70 } 71 72 LL getSum(int p, int c) { 73 LL a = (mpow(p, c + 1) - 1); 74 LL b = inv(p - 1, moder); 75 return (a * b) % moder; 76 } 77 78 LL res = 1; 79 inline void solve() { 80 for(int i = 1, x; i <= n; i++) { 81 x = arr[i]; 82 for(int j = 0; prime[j] * prime[j] <= x && arr[i] > 1; j++) { 83 if((arr[i] % prime[j]) == 0) { 84 ds[cnt].first = prime[j], ds[cnt].second = 0; 85 while((arr[i] % prime[j]) == 0) 86 arr[i] /= prime[j], ds[cnt].second++; 87 cnt++; 88 } 89 } 90 if(arr[i] > 1) 91 ds[cnt].first = arr[i], ds[cnt++].second = 1; 92 } 93 sort(ds, ds + cnt); 94 95 int p, c; 96 for(int id = 0; id < cnt; ) { 97 p = ds[id].first; 98 LL P = 1; 99 for(int i = id; (id < cnt && ds[i].first == ds[id].first) ? (true) : (id = i, false); i++) { 100 c = ds[i].second; 101 P = (P * getSum(p, c)) % moder; 102 } 103 P = ((P * (p - 1) + 1) % moder) * inv(p, moder) % moder; 104 res = (res * P) % moder; 105 } 106 printf(Auto, res); 107 } 108 109 int main() { 110 Euler(); 111 init(); 112 solve(); 113 return 0; 114 }
