Codeforces 438D The Child and Sequence - 线段树

At the children's day, the child came to Picks's house, and messed his house up. Picks was angry at him. A lot of important things were lost, in particular the favorite sequence of Picks.

Fortunately, Picks remembers how to repair the sequence. Initially he should create an integer array a[1], a[2], ..., a[n]. Then he should perform a sequence of m operations. An operation can be one of the following:

  1. Print operation l, r. Picks should write down the value of .
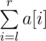  2. Modulo operation l, r, x. Picks should perform assignment a[i] = a[i] mod x for each i (l ≤ i ≤ r).
  3. Set operation k, x. Picks should set the value of a[k] to x (in other words perform an assignment a[k] = x).

Can you help Picks to perform the whole sequence of operations?

Input

The first line of input contains two integer: n, m (1 ≤ n, m ≤ 105). The second line contains n integers, separated by space: a[1], a[2], ..., a[n] (1 ≤ a[i] ≤ 109) — initial value of array elements.

Each of the next m lines begins with a number type .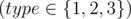

  • If type = 1, there will be two integers more in the line: l, r (1 ≤ l ≤ r ≤ n), which correspond the operation 1.
  • If type = 2, there will be three integers more in the line: l, r, x (1 ≤ l ≤ r ≤ n; 1 ≤ x ≤ 109), which correspond the operation 2.
  • If type = 3, there will be two integers more in the line: k, x (1 ≤ k ≤ n; 1 ≤ x ≤ 109), which correspond the operation 3.
Output

For each operation 1, please print a line containing the answer. Notice that the answer may exceed the 32-bit integer.

Examples
Input
5 5 1 2 3 4 5 2 3 5 4 3 3 5 1 2 5 2 1 3 3 1 1 3
Output
8 5
Input
10 10 6 9 6 7 6 1 10 10 9 5 1 3 9 2 7 10 9 2 5 10 8 1 4 7 3 3 7 2 7 9 9 1 2 4 1 6 6 1 5 9 3 1 10
Output
49 15 23 1 9
Note

Consider the first testcase:

  • At first, a = {1, 2, 3, 4, 5}.
  • After operation 1, a = {1, 2, 3, 0, 1}.
  • After operation 2, a = {1, 2, 5, 0, 1}.
  • At operation 3, 2 + 5 + 0 + 1 = 8.
  • After operation 4, a = {1, 2, 2, 0, 1}.
  • At operation 5, 1 + 2 + 2 = 5.

　　题目大意 维护一个数列，有3种操作，分别是区间求和，区间取模和单点修改。

　　显然线段树(请不要问我为什么。。。学长的Tag打在那儿的)

　　区间求和和单点修改都是线段树的拿手好戏，但是对于区间取模似乎不是那么好做。考虑可以区间批量更新sum吗？显然不行。

　　但是考虑到这里只有单点修改，而且对一个大于模数的数取模，它的值至多为它原来的值的一半。

　　所以区间记录一个最大值剪枝，每次区间取模先判断是否有必要进行递归取模，如果有，就暴力递归下去，在底层修改。

Code

  1 /**
  2  * Codeforces
  3  * Problem#438D
  4  * Accepted
  5  * Time: 436ms
  6  * Memory: 8740k
  7  */
  8 #include <bits/stdc++.h>
  9 #ifndef WIN32
 10 #define Auto "%lld"
 11 #else
 12 #define Auto "%I64d"
 13 #endif
 14 using namespace std;
 15 
 16 typedef class SegTreeNode {
 17     public:
 18         int maxv;
 19         long long sum;
 20         SegTreeNode *l, *r;
 21         
 22         SegTreeNode():maxv(0), sum(0), l(NULL), r(NULL) {        }
 23         
 24         inline void pushUp() {
 25             maxv = max(l->maxv, r->maxv);
 26             sum = l->sum + r->sum; 
 27         }
 28 }SegTreeNode;
 29 
 30 typedef class SegTree {
 31     public:
 32         SegTreeNode* root;
 33         
 34         SegTree():root(NULL) {        }
 35         SegTree(int n, int* a) {
 36             build(root, 1, n, a);
 37         }
 38         
 39         void build(SegTreeNode*& node, int l, int r, int* a) {
 40             node = new SegTreeNode();
 41             if(l == r) {
 42                 node->sum = node->maxv = a[l];
 43                 return;
 44             }
 45             int mid = (l + r) >> 1;
 46             build(node->l, l, mid, a);
 47             build(node->r, mid + 1, r, a);
 48             node->pushUp();
 49         }
 50         
 51         void update(SegTreeNode*& node, int l, int r, int idx, int val) {
 52             if(l == r) {
 53                 node->maxv = node->sum = val;
 54                 return;
 55             }
 56             int mid = (l + r) >> 1;
 57             if(idx <= mid)    update(node->l, l, mid, idx, val);
 58             else update(node->r, mid + 1, r, idx, val);
 59             node->pushUp();
 60         }
 61         
 62         void update(SegTreeNode*& node, int l, int r, int ql, int qr, int moder) {
 63             if(l == r) {
 64                 node->maxv = (node->sum %= moder);
 65                 return;
 66             }
 67             int mid = (l + r) >> 1;
 68             if(qr <= mid && node->l->maxv >= moder)    update(node->l, l, mid, ql, qr, moder);
 69             else if(ql > mid && node->r->maxv >= moder)    update(node->r, mid + 1, r, ql, qr, moder);
 70             else if(qr > mid && ql <= mid) {
 71                 if(node->l->maxv >= moder)
 72                     update(node->l, l, mid, ql, mid, moder);
 73                 if(node->r->maxv >= moder)
 74                     update(node->r, mid + 1, r, mid + 1, qr, moder);
 75             }
 76             node->pushUp();
 77         }
 78         
 79         long long query(SegTreeNode*& node, int l, int r, int ql, int qr) {
 80             if(l == ql && r == qr) {
 81                 return node->sum;
 82             }
 83             int mid = (l + r) >> 1;
 84             if(qr <= mid)    return query(node->l, l, mid, ql, qr);
 85             if(ql > mid)    return query(node->r, mid + 1, r, ql, qr);
 86                 return query(node->l, l, mid, ql, mid) + query(node->r, mid + 1, r, mid + 1, qr);
 87             }              
 88 }SegTree;              
 89                        
 90 int n, m;              
 91 int* arr;              
 92 SegTree st;            
 93 inline void init() {
 94     scanf("%d%d", &n, &m);
 95     arr = new int[(n + 1)];
 96     for(int i = 1; i <= n; i++)
 97         scanf("%d", arr + i);
 98     st = SegTree(n, arr);
 99 }                      
100 
101 inline void solve() {
102     int opt, a, b, c;
103     while(m--) {
104         scanf("%d%d%d", &opt, &a, &b);
105         if(opt == 1) {
106             printf(Auto"\n", st.query(st.root, 1, n, a, b));
107         } else if(opt == 2) {
108             scanf("%d", &c);
109             st.update(st.root, 1, n, a, b, c);
110         } else {
111             st.update(st.root, 1, n, a, b);
112         }
113     }
114 }
115 
116 int main() {
117     init();
118     solve();
119     return 0;
120 }

 

posted @ 2017-08-01 13:52  阿波罗2003  阅读(286)  评论(0)  编辑  收藏  举报