bzoj 2724 [Violet 6]蒲公英 - 分块

Description

 

Input

修正一下

l = (l_0 + x - 1) mod n + 1, r = (r_0 + x - 1) mod n + 1

Output

Sample Input

6 3
1 2 3 2 1 2
1 5
3 6
1 5

Sample Output

1
2
1

HINT

 


修正下：


n <= 40000, m <= 50000

 

Source

Vani原创

　　题目大意 强制在线区间众数(第一次如此简洁明了的题目大意)。

　　首先思考主席树和线段树等等数据结构，然后发现区间众数没有可减性，合并时间复杂度有很高，然后我就不会了。

　　然后瞄了下数据范围，支持分块大暴力诶！

　　根据分块常用套路，分块的目标是完整的块内快速出答案，然后两边暴力枚举，所以记录如下两个数组

　　cnt[i][j] 数j在前i块中出现的次数。

　　ans[i][j] 第i块到第j块的区间众数。

　　然而ai <= 1e9，cnt直接MLE，所以要先让离散化整个数组，输出答案的时候映射一下（或者你迷之WA掉这道题）就好了。

　　这两个都可以暴力，第一个没什么说头，第二就枚举后缀(外层循环i，内层直接枚举第i块开始的元素到数组末尾，边数数，然后更新当前众数，到一个块的结尾再更新答案)，然而开始我把第二个的暴力的复杂度算错了，就差点不会做了，注意每次内层for的时候要先memset。

　　查询的时候因为有前缀和，完整的部分的数量可以O(1)算出，再记录一下两边的counter，边枚边更新答案即可。

　　因为直接memset会TLE，所以要用一点黑科技，因为枚举的点很少，所以用一个vector记录所有更新的点，然后枚举结束后，把vector中的元素指向的位置挨个设成0。

　　预处理的时间复杂度显然是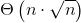,单次查询至多枚举的元素是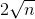个，中间的查询时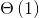的，所以总时间复杂度为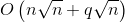

Code

  1 /**
  2  * bzoj
  3  * Problem#2724
  4  * Accepted
  5  * Time:5960ms
  6  * Memory:10304k
  7  */
  8 #include <iostream>
  9 #include <cstdio>
 10 #include <ctime>
 11 #include <cmath>
 12 #include <cctype>
 13 #include <cstring>
 14 #include <cstdlib>
 15 #include <fstream>
 16 #include <sstream>
 17 #include <algorithm>
 18 #include <map>
 19 #include <set>
 20 #include <stack>
 21 #include <queue>
 22 #include <vector>
 23 #include <stack>
 24 #ifndef WIN32
 25 #define Auto "%lld"
 26 #else
 27 #define Auto "%I64d"
 28 #endif
 29 using namespace std;
 30 typedef bool boolean;
 31 const signed int inf = (signed)((1u << 31) - 1);
 32 const signed long long llf = (signed long long)((1ull << 63) - 1);
 33 const double eps = 1e-6;
 34 const int binary_limit = 128;
 35 #define smin(a, b) a = min(a, b)
 36 #define smax(a, b) a = max(a, b)
 37 #define max3(a, b, c) max(a, max(b, c))
 38 #define min3(a, b, c) min(a, min(b, c))
 39 template<typename T>
 40 inline boolean readInteger(T& u){
 41     char x;
 42     int aFlag = 1;
 43     while(!isdigit((x = getchar())) && x != '-' && x != -1);
 44     if(x == -1) {
 45         ungetc(x, stdin);    
 46         return false;
 47     }
 48     if(x == '-'){
 49         x = getchar();
 50         aFlag = -1;
 51     }
 52     for(u = x - '0'; isdigit((x = getchar())); u = (u * 10) + x - '0');
 53     ungetc(x, stdin);
 54     u *= aFlag;
 55     return true;
 56 }
 57 
 58 template<typename T>class Matrix{
 59     public:
 60         T *p;
 61         int lines;
 62         int rows;
 63         Matrix():p(NULL){    }
 64         Matrix(int rows, int lines):lines(lines), rows(rows){
 65             p = new T[(lines * rows)];
 66         }
 67         T* operator [](int pos){
 68             return (p + pos * lines);
 69         }
 70 };
 71 #define matset(m, i, s) memset((m).p, (i), (s) * (m).lines * (m).rows)
 72 
 73 
 74 int n, m, q;
 75 int cs, cc = 0;
 76 int* a;
 77 int* sa;
 78 int* keyer;
 79 Matrix<int> cnt;
 80 
 81 inline void init() {
 82     readInteger(n);
 83     readInteger(q);
 84     cs = sqrt(n + 0.5);
 85     a = new int[(n + 1)];
 86     for(int i = 0, s = 0; i < n; i++) {
 87         readInteger(a[i]);
 88         if(s <= i) cc++, s += cs;
 89     }
 90 }
 91 
 92 inline void descrete() {
 93     sa = new int[(n + 1)];
 94     memcpy(sa, a, sizeof(int) * n);
 95     sort(sa, sa + n);
 96     m = unique(sa, sa + n) - sa - 1;
 97     keyer = new int[(m + 1)];
 98     for(int i = 0; i <= m; i++)
 99         keyer[i] = sa[i];
100     for(int i = 0; i < n; i++)
101         a[i] = lower_bound(sa, sa + m + 1, a[i]) - sa;
102 }
103 
104 Matrix<int> ans;
105 int* counter;
106 inline void init_chunks() {
107     ans = Matrix<int>(cc + 1, cc + 1);
108     matset(ans, 0, sizeof(int));
109     int zs = 0;
110     counter = new int[(m + 1)];
111     for(int i = 0; i < cc; i++) {
112         memset(counter, 0, sizeof(int) * (m + 1));
113         for(int j = cs * i; j < n; j++) {
114             counter[a[j]]++;
115             if(counter[a[j]] > counter[zs] || (counter[a[j]] == counter[zs] && a[j] < zs))
116                 zs = a[j];
117             if(j % cs == cs - 1 || j == n - 1) {
118                 int endid = j / cs;
119                 ans[i][endid] = zs;
120             }
121         }
122     }
123     
124     cnt = Matrix<int>(cc, m + 1);
125     matset(cnt, 0, sizeof(int));
126     memset(counter, 0, sizeof(int) * (m + 1));
127     for(int i = 0; i < n; i++)
128         cnt[i / cs][a[i]]++;
129     
130     for(int i = 1; i < cc; i++) {
131         for(int j = 0; j <= m; j++)
132             cnt[i][j] += cnt[i - 1][j];
133     }
134 }
135 
136 vector<int> modified;
137 inline void solve() {
138     int last = 0, l, r;
139 //    int debugc = 0;
140     while(q--) {
141         readInteger(l);
142         readInteger(r);
143 //        l--, r--;
144         l = (l + last - 1) % n;
145         r = (r + last - 1) % n;
146         if(l > r)    swap(l, r);
147         if(l / cs == r / cs || l / cs + 1 == r / cs) {
148             int zs = 0;
149             for(int i = l; i <= r; i++/*, debugc++*/) {
150                 counter[a[i]]++;
151                 modified.push_back(a[i]);
152                 if(counter[a[i]] > counter[zs] || (counter[a[i]] == counter[zs] && a[i] < zs))
153                     zs = a[i];
154             }
155             for(int i = 0; i < (signed)modified.size(); i++/*, debugc++*/)
156                 counter[modified[i]] = 0;
157             modified.clear();
158             last = keyer[zs];
159             printf("%d\n", keyer[zs]);
160         } else {
161             int le = l / cs, rg = r / cs, zs = ans[le + 1][rg - 1];
162             for(int i = l; i < (le + 1) * cs; i++/*, debugc++*/) {
163                 counter[a[i]]++;
164                 modified.push_back(a[i]);
165                 if(counter[a[i]] + cnt[rg - 1][a[i]] - cnt[le][a[i]] > counter[zs] + cnt[rg - 1][zs] - cnt[le][zs] ||
166                  (counter[a[i]] + cnt[rg - 1][a[i]] - cnt[le][a[i]] == counter[zs] + cnt[rg - 1][zs] - cnt[le][zs] && a[i] < zs))    zs = a[i];
167             }
168             for(int i = rg * cs; i <= r; i++/*, debugc++*/) {
169                 counter[a[i]]++;
170                 modified.push_back(a[i]);
171                 if(counter[a[i]] + cnt[rg - 1][a[i]] - cnt[le][a[i]] > counter[zs] + cnt[rg - 1][zs] - cnt[le][zs] ||
172                  (counter[a[i]] + cnt[rg - 1][a[i]] - cnt[le][a[i]] == counter[zs] + cnt[rg - 1][zs] - cnt[le][zs] && a[i] < zs))    zs = a[i];
173             }
174             for(int i = 0; i < (signed)modified.size(); i++/*, debugc++*/)
175                 counter[modified[i]] = 0;
176             modified.clear();
177             last = keyer[zs];
178             printf("%d\n", keyer[zs]);
179         }
180 //        fprintf(stderr, "%d, %d\n", q, debugc);
181     }
182 }
183 
184 int main() {
185 //    freopen("a.in", "r", stdin);
186 //    freopen("a.out", "w", stdout);
187     init();
188     descrete();
189     init_chunks();
190     solve();
191     return 0;
192 }
posted @ 2017-07-21 12:17  阿波罗2003  阅读(180)  评论(0)  编辑  收藏  举报