Codeforces 817C Really Big Numbers - 二分法 - 数论
Ivan likes to learn different things about numbers, but he is especially interested in really big numbers. Ivan thinks that a positive integer number x is really big if the difference between x and the sum of its digits (in decimal representation) is not less than s. To prove that these numbers may have different special properties, he wants to know how rare (or not rare) they are — in fact, he needs to calculate the quantity of really big numbers that are not greater than n.
Ivan tried to do the calculations himself, but soon realized that it's too difficult for him. So he asked you to help him in calculations.
The first (and the only) line contains two integers n and s (1 ≤ n, s ≤ 1018).
Print one integer — the quantity of really big numbers that are not greater than n.
12 1
3
25 20
0
10 9
1
In the first example numbers 10, 11 and 12 are really big.
In the second example there are no really big numbers that are not greater than 25 (in fact, the first really big number is 30: 30 - 3 ≥ 20).
In the third example 10 is the only really big number (10 - 1 ≥ 9).
题目大意 设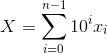 ,
, 定义
定义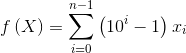 ,求满足
,求满足 的X有 多少个。
的X有 多少个。
随便举几个数10, 20, 30, 100,然后发现对应的函数值的分别为9, 18, 27和99猜测它满足"单调性"。
现在来证明一下,当A > B时,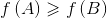 。
。
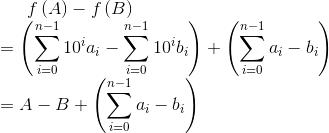
当最高的不相同的位数为k,则A - B的最小值为$10^{k - 1}$,后面的各位数字之差最小为 -9(k - 1)(个位为第1位),显然这两个数的和大于等于0。
所以就可以二分出第一个满足要求的数,然后算一算就好了。
Code
1 #include <iostream> 2 #include <cstdio> 3 #include <ctime> 4 #include <cmath> 5 #include <cctype> 6 #include <cstring> 7 #include <cstdlib> 8 #include <fstream> 9 #include <sstream> 10 #include <algorithm> 11 #include <map> 12 #include <set> 13 #include <stack> 14 #include <queue> 15 #include <vector> 16 #include <stack> 17 #ifndef WIN32 18 #define Auto "%lld" 19 #else 20 #define Auto "%I64d" 21 #endif 22 using namespace std; 23 typedef bool boolean; 24 const signed int inf = (signed)((1u << 31) - 1); 25 const signed long long llf = (signed long long)((1ull << 63) - 1); 26 const double eps = 1e-6; 27 const int binary_limit = 128; 28 #define smin(a, b) a = min(a, b) 29 #define smax(a, b) a = max(a, b) 30 #define max3(a, b, c) max(a, max(b, c)) 31 #define min3(a, b, c) min(a, min(b, c)) 32 template<typename T> 33 inline boolean readInteger(T& u){ 34 char x; 35 int aFlag = 1; 36 while(!isdigit((x = getchar())) && x != '-' && x != -1); 37 if(x == -1) { 38 ungetc(x, stdin); 39 return false; 40 } 41 if(x == '-'){ 42 x = getchar(); 43 aFlag = -1; 44 } 45 for(u = x - '0'; isdigit((x = getchar())); u = (u * 10) + x - '0'); 46 ungetc(x, stdin); 47 u *= aFlag; 48 return true; 49 } 50 51 #define LL long long 52 53 LL n, s; 54 55 inline void init() { 56 readInteger(n); 57 readInteger(s); 58 } 59 60 boolean check(LL x) { 61 LL y = x, bitsum = 0; 62 while(y) bitsum += y % 10, y /= 10; 63 return x - bitsum >= s; 64 } 65 66 inline void solve() { 67 LL l = 1, r = n; 68 while(l <= r) { 69 LL mid = (l + r) >> 1; 70 if(check(mid)) r = mid - 1; 71 else l = mid + 1; 72 } 73 printf(Auto"\n", n - r); 74 } 75 76 int main() { 77 init(); 78 solve(); 79 return 0; 80 }

