Codeforces Round #423 (Div. 2, rated, based on VK Cup Finals) Problem E (Codeforces 828E) - 分块

Everyone knows that DNA strands consist of nucleotides. There are four types of nucleotides: "A", "T", "G", "C". A DNA strand is a sequence of nucleotides. Scientists decided to track evolution of a rare species, which DNA strand was string s initially.

Evolution of the species is described as a sequence of changes in the DNA. Every change is a change of some nucleotide, for example, the following change can happen in DNA strand "AAGC": the second nucleotide can change to "T" so that the resulting DNA strand is "ATGC".

Scientists know that some segments of the DNA strand can be affected by some unknown infections. They can represent an infection as a sequence of nucleotides. Scientists are interested if there are any changes caused by some infections. Thus they sometimes want to know the value of impact of some infection to some segment of the DNA. This value is computed as follows:

• Let the infection be represented as a string e, and let scientists be interested in DNA strand segment starting from position l to position r, inclusive.
• Prefix of the string eee... (i.e. the string that consists of infinitely many repeats of string e) is written under the string s from position lto position r, inclusive.
• The value of impact is the number of positions where letter of string s coincided with the letter written under it.

Being a developer, Innokenty is interested in bioinformatics also, so the scientists asked him for help. Innokenty is busy preparing VK Cup, so he decided to delegate the problem to the competitors. Help the scientists!

Input

The first line contains the string s (1 ≤ |s| ≤ 10⁵) that describes the initial DNA strand. It consists only of capital English letters "A", "T", "G" and "C".

The next line contains single integer q (1 ≤ q ≤ 10⁵) — the number of events.

After that, q lines follow, each describes one event. Each of the lines has one of two formats:

• 1 x c, where x is an integer (1 ≤ x ≤ |s|), and c is a letter "A", "T", "G" or "C", which means that there is a change in the DNA: the nucleotide at position x is now c.
• 2 l r e, where l, r are integers (1 ≤ l ≤ r ≤ |s|), and e is a string of letters "A", "T", "G" and "C" (1 ≤ |e| ≤ 10), which means that scientists are interested in the value of impact of infection e to the segment of DNA strand from position l to position r, inclusive.

Output

For each scientists' query (second type query) print a single integer in a new line — the value of impact of the infection on the DNA.

Examples

input

ATGCATGC
4
2 1 8 ATGC
2 2 6 TTT
1 4 T
2 2 6 TA

output

8
2
4

input

GAGTTGTTAA
6
2 3 4 TATGGTG
1 1 T
1 6 G
2 5 9 AGTAATA
1 10 G
2 2 6 TTGT

output

0
3
1

Note

Consider the first example. In the first query of second type all characters coincide, so the answer is 8. In the second query we compare string "TTTTT..." and the substring "TGCAT". There are two matches. In the third query, after the DNA change, we compare string "TATAT..."' with substring "TGTAT". There are 4 matches.

---

　　我告诉我同学我用分块把这道题A掉了，我同学喷我为毛不去打比赛，我表示这场比赛A,B题好坑啊。。

　　不多扯废话了。

　　题目大意 给定一个字符串和一些操作。操作是修改字符串某个位置的字符，查询是给定一个比较短的字符串从这个字符串的a位置开始，一直到b位置，循环这个较短的字符串进行逐字节比较，输出匹配的字符数。

　　不难想到用各种线段树，树状数组，然而为了简单粗暴，我选择了分块(显然树状数组做起来更简单)。

　　根据常用套路，很容易得到每个块要记录下标模1到模10的余数为r，字符为c的出现次数。

　　初始化块的时候暴力3重for去统计。修改时for模数，然后按意思修改一下就好了(注意字符串也要改)。

　　查询时，先判断起始是否在同一块中，如果在，直接暴力for去算答案。否则就暴力for块两端的部分，中间暴力枚举块存储的数据，根据模查询字符串长度下的模数去统计(我也不好说清楚，是在不懂可以看代码，如果还不懂，就在评论区问一下吧)。

　　总时间复杂度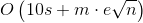

Code

/**
 * Codeforces
 * Problem#828E
 * Accepted
 * Time:1107ms
 * Memory:4104k
 */
#include <iostream>
#include <cstdio>
#include <ctime>
#include <cmath>
#include <cctype>
#include <cstring>
#include <cstdlib>
#include <fstream>
#include <sstream>
#include <algorithm>
#include <map>
#include <set>
#include <stack>
#include <queue>
#include <vector>
#include <stack>
#ifndef WIN32
#define Auto "%lld"
#else
#define Auto "%I64d"
#endif
using namespace std;
typedef bool boolean;
const signed int inf = (signed)((1u << 31) - 1);
const signed long long llf = (signed long long)((1ull << 61) - 1);
const double eps = 1e-6;
const int binary_limit = 128;
#define smin(a, b) a = min(a, b)
#define smax(a, b) a = max(a, b)
#define max3(a, b, c) max(a, max(b, c))
#define min3(a, b, c) min(a, min(b, c))
template<typename T>
inline boolean readInteger(T& u){
    char x;
    int aFlag = 1;
    while(!isdigit((x = getchar())) && x != '-' && x != -1);
    if(x == -1) {
        ungetc(x, stdin);    
        return false;
    }
    if(x == '-'){
        x = getchar();
        aFlag = -1;
    }
    for(u = x - '0'; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - '0');
    ungetc(x, stdin);
    u *= aFlag;
    return true;
}

int cti(char x) {
    if(x == 'A')    return 0;
    if(x == 'C')    return 1;
    if(x == 'G')    return 2;
    return 3;
}

typedef class Chunk {
    public:
        int id;
        int counter[11][11][4];        // moder, rest, character
        
        Chunk() {        };
        Chunk(int id):id(id) {
            memset(counter, 0, sizeof(counter));
        }
}Chunk;

int n, m;
int cs, cc;
char s[100005];
vector<Chunk> lis;

inline void init() {
    gets(s);
    readInteger(n);
    m = strlen(s);
    cs = (int)sqrt(m + 0.5);
}

inline int disposeWithBeginning(int a, char* buf, int len) {
    int sid = a / cs, ret = 0;
    for(int i = a; i < (sid + 1) * cs; i++) {
        if(s[i] == buf[(i - a) % len])
            ret++;
    }
    return ret;
}

inline int disposeWithEnding(int a, int b, char* buf, int len) {
    int eid = b / cs, ret = 0;
    for(int i = eid * cs; i <= b; i++) {
        if(s[i] == buf[(i - a) % len])
            ret++;
    }
    return ret;
}

inline void init_chunks() {
    for(cc = 0; cc * cs <= m; cc++) {
        Chunk b(cc);
        for(int mod = 1; mod <= 10; mod++) {
            for(int rest = 0; rest < mod; rest++) {
                int start_pos = cc * cs - (cc * cs) % mod + rest;
                if(start_pos < cc * cs)    start_pos += mod;
                for(int i = start_pos; i < (cc + 1) * cs; i += mod)
                    b.counter[mod][rest][cti(s[i])]++;
            }
        }
        lis.push_back(b);
    }
}

inline void solve() {
    int opt, a, b, len, res;
    char buf[15];
    while(n--) {
        readInteger(opt);
        readInteger(a);
        a--;
        if(opt == 1) {
            scanf("%s", buf);
            int bid = a / cs;
            char bchar = s[a];
            for(int mod = 1; mod <= 10; mod++) {
                b = a % mod;
                lis[bid].counter[mod][b][cti(buf[0])]++, lis[bid].counter[mod][b][cti(bchar)]--;
            }
            s[a] = buf[0];
        } else {
            res = 0;
            readInteger(b);
            b--;
            scanf("%s", buf);
            len = strlen(buf);
            int sid = a / cs, eid = b / cs;
            if(sid == eid) {
                for(int i = a; i <= b; i++) {
                    if(s[i] == buf[(i - a) % len])
                        res++;
                }
            } else {
                for(int i = sid + 1; i < eid; i++) {
                    int base = (i * cs - a) % len;
                    int rbase = (i * cs) % len;
                    for(int j = 0; j < len; j++) {
                        res += lis[i].counter[len][(rbase + j) % len][cti(buf[(base + j) % len])];
                    }
                }
                res += disposeWithBeginning(a, buf, len);
                res += disposeWithEnding(a, b, buf, len);
            }
            printf("%d\n", res);
        }
    }
}

int main() {
    init();
    init_chunks();
    solve();
    return 0;
}