Codeforces 828D High Load - 贪心

Arkady needs your help again! This time he decided to build his own high-speed Internet exchange point. It should consist of n nodes connected with minimum possible number of wires into one network (a wire directly connects two nodes). Exactly k of the nodes should be exit-nodes, that means that each of them should be connected to exactly one other node of the network, while all other nodes should be connected to at least two nodes in order to increase the system stability.

Arkady wants to make the system as fast as possible, so he wants to minimize the maximum distance between two exit-nodes. The distance between two nodes is the number of wires a package needs to go through between those two nodes.

Help Arkady to find such a way to build the network that the distance between the two most distant exit-nodes is as small as possible.

Input

The first line contains two integers n and k (3 ≤ n ≤ 2·10⁵, 2 ≤ k ≤ n - 1) — the total number of nodes and the number of exit-nodes.

Note that it is always possible to build at least one network with n nodes and k exit-nodes within the given constraints.

Output

In the first line print the minimum possible distance between the two most distant exit-nodes. In each of the next n - 1 lines print two integers: the ids of the nodes connected by a wire. The description of each wire should be printed exactly once. You can print wires and wires' ends in arbitrary order. The nodes should be numbered from 1 to n. Exit-nodes can have any ids.

If there are multiple answers, print any of them.

Examples

input

3 2

output

2
1 2
2 3

input

5 3

output

3
1 2
2 3
3 4
3 5

Note

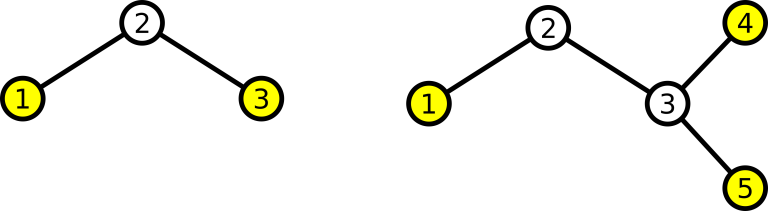
In the first example the only network is shown on the left picture.

In the second example one of optimal networks is shown on the right picture.

Exit-nodes are highlighted.

 

---

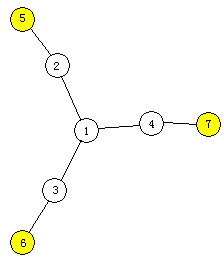
　　直接贪心，目标是形成一个"菊花图"，中间一个点，然后其它点周围一圈一圈地"围"着它。

　　比如当n = 7, k = 3时，形成下面的一棵树

　　计算的时候稍微判断一下n模k的余数(当被整除、余1和余数大于2的结果是不同的)然后特判一下就好了(详情可以看代码)。

Code

/**
 * Codeforces
 * Problem#828D
 * Accepted
 * Time:78ms
 * Memory:2052k
 */
#include <iostream>
#include <cstdio>
#include <ctime>
#include <cmath>
#include <cctype>
#include <cstring>
#include <cstdlib>
#include <fstream>
#include <sstream>
#include <algorithm>
#include <map>
#include <set>
#include <stack>
#include <queue>
#include <vector>
#include <stack>
#ifndef WIN32
#define Auto "%lld"
#else
#define Auto "%I64d"
#endif
using namespace std;
typedef bool boolean;
const signed int inf = (signed)((1u << 31) - 1);
const signed long long llf = (signed long long)((1ull << 61) - 1);
const double eps = 1e-6;
const int binary_limit = 128;
#define smin(a, b) a = min(a, b)
#define smax(a, b) a = max(a, b)
#define max3(a, b, c) max(a, max(b, c))
#define min3(a, b, c) min(a, min(b, c))
template<typename T>
inline boolean readInteger(T& u){
    char x;
    int aFlag = 1;
    while(!isdigit((x = getchar())) && x != '-' && x != -1);
    if(x == -1) {
        ungetc(x, stdin);    
        return false;
    }
    if(x == '-'){
        x = getchar();
        aFlag = -1;
    }
    for(u = x - '0'; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - '0');
    ungetc(x, stdin);
    u *= aFlag;
    return true;
}

int n, k;

inline void init() {
    readInteger(n);
    readInteger(k);
}

inline void solve() {
    int temp = (n - 1);
    int res = temp / k;
    if(temp % k == 1)    res = res * 2 + 1;
    else if(temp % k >= 2)    res = res * 2 + 2;
    else res = res * 2;
    printf("%d\n", res);
    for(int i = 2; i <= k + 1; i++)
        printf("1 %d\n", i);
    for(int i = k + 2; i <= n; i++) {
        printf("%d %d\n", i - k, i);
    }
}

int main() {
    init();
    solve();
    return 0;
}