poj 3207 Ikki's Story IV - Panda's Trick - 2-sat

liympanda, one of Ikki’s friend, likes playing games with Ikki. Today after minesweeping with Ikki and winning so many times, he is tired of such easy games and wants to play another game with Ikki.

liympanda has a magic circle and he puts it on a plane, there are n points on its boundary in circular border: 0, 1, 2, …, n − 1. Evil panda claims that he is connecting m pairs of points. To connect two points, liympanda either places the link entirely inside the circle or entirely outside the circle. Now liympanda tells Ikki no two links touch inside/outside the circle, except on the boundary. He wants Ikki to figure out whether this is possible…

Despaired at the minesweeping game just played, Ikki is totally at a loss, so he decides to write a program to help him.

Input

The input contains exactly one test case.

In the test case there will be a line consisting of of two integers: n and m (n ≤ 1,000, m ≤ 500). The following m lines each contain two integers a_i and b_i, which denote the endpoints of the ith wire. Every point will have at most one link.

Output

Output a line, either “panda is telling the truth...” or “the evil panda is lying again”.

Sample Input

4 2
0 1
3 2

Sample Output

panda is telling the truth...

---

　　题目大意 圆上有n个点，从左至右依次编号为0, 1, 2, ..., n - 1。给出m对点的编号，连接这m对点(连线只能全在圆外或者圆内)，问是否可以使得这m条连线不相交。

　　首先看一下可能会相交的情况:

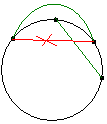
　　即存在两对点l₁和r₁,l₂和r₂，且满足。

　　我们将每条连线拆成2个点，(2 * i - 1)和2 * i，表示在圆内还是在圆外。于是这道题就转化成了2-sat问题。Tarjan完了缩点，再判断是否存在每条连线对应的两个点在同一强连通分量内，如果有，则无解，否则有解。

Code

/**
 * poj
 * Problem#3207
 * Accepted
 * Time:32ms
 * Memory:8604k
 */
#include <iostream>
#include <cstdio>
#include <ctime>
#include <cmath>
#include <cctype>
#include <cstring>
#include <cstdlib>
#include <fstream>
#include <sstream>
#include <algorithm>
#include <map>
#include <set>
#include <stack>
#include <queue>
#include <vector>
#include <stack>
#ifndef WIN32
#define Auto "%lld"
#else
#define Auto "%I64d"
#endif
using namespace std;
typedef bool boolean;
const signed int inf = (signed)((1u << 31) - 1);
const double eps = 1e-6;
const int binary_limit = 128;
#define smin(a, b) a = min(a, b)
#define smax(a, b) a = max(a, b)
#define max3(a, b, c) max(a, max(b, c))
#define min3(a, b, c) min(a, min(b, c))
template<typename T>
inline boolean readInteger(T& u){
    char x;
    int aFlag = 1;
    while(!isdigit((x = getchar())) && x != '-' && x != -1);
    if(x == -1) {
        ungetc(x, stdin);    
        return false;
    }
    if(x == '-'){
        x = getchar();
        aFlag = -1;
    }
    for(u = x - '0'; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - '0');
    ungetc(x, stdin);
    u *= aFlag;
    return true;
}

///map template starts
typedef class Edge{
    public:
        int end;
        int next;
        Edge(const int end = 0, const int next = 0):end(end), next(next){}
}Edge;

typedef class MapManager{
    public:
        int ce;
        int *h;
        Edge *edge;
        MapManager(){}
        MapManager(int points, int limit):ce(0){
            h = new int[(const int)(points + 1)];
            edge = new Edge[(const int)(limit + 1)];
            memset(h, 0, sizeof(int) * (points + 1));
        }
        inline void addEdge(int from, int end){
            edge[++ce] = Edge(end, h[from]);
            h[from] = ce;
        }
        inline void addDoubleEdge(int from, int end){
            addEdge(from, end);
            addEdge(end, from);
        }
        Edge& operator [] (int pos) {
            return edge[pos];
        }
}MapManager;
#define m_begin(g, i) (g).h[(i)]
///map template ends

int n, m;
MapManager g;
int *ls, *rs;

inline void init() {
    readInteger(n);
    readInteger(m);
    ls = new int[(m + 1)];
    rs = new int[(m + 1)];
    for(int i = 1; i <= m; i++) {
        readInteger(ls[i]);
        readInteger(rs[i]);
        if(ls[i] > rs[i])
            swap(ls[i], rs[i]);
    }
}

inline void init_map() {
    g = MapManager(2 * m + 3, 2 * n * m);
    for(int i = 1; i < m; i++) {
        for(int j = i + 1; j <= m; j++) {
            if(ls[i] <= ls[j] && rs[i] >= ls[j] && rs[i] <= rs[j]) {
                g.addDoubleEdge(2 * i - 1, 2 * j);
                g.addDoubleEdge(2 * j - 1, 2 * i);
            }
        }
    }
}

int cnt = 0;
int* visitID;
int* exitID;
boolean* visited;
boolean* instack;
stack<int> s;
int* belong;
inline void init_tarjan() {
    int an = 2 * m + 3;
    visitID = new int[(an)];
    exitID = new int[(an)];
    visited = new boolean[(an)];
    instack = new boolean[(an)];
    belong = new int[(an)];
    memset(visited, false, sizeof(boolean) * an);
    memset(instack, false, sizeof(boolean) * an);
}

void tarjan(int node) {
    visitID[node] = exitID[node] = cnt++;
    visited[node] = instack[node] = true;
    s.push(node);
    
    for(int i = m_begin(g, node); i; i = g[i].next) {
        int& e = g[i].end;
        if(!visited[e]) {
            tarjan(e);
            smin(exitID[node], exitID[e]);
        } else if(instack[e]) {
            smin(exitID[node], visitID[e]);
        }
    }
    
    if(visitID[node] == exitID[node]) {
        int now = -1;
        while(now != node) {
            now = s.top();
            s.pop();
            instack[now] = false;
            belong[now] = node;
        }
    }
}

inline void solve() {
    for(int i = 1; i < (m << 1); i += 2)
        if(belong[i] == belong[i + 1]) {
            puts("the evil panda is lying again");
            return;
        }
    puts("panda is telling the truth...");
}

int main() {
    init();
    init_map();
    init_tarjan();
    for(int i = 1; i <= 2 * m; i++)
        if(!visited[i])
            tarjan(i);
    solve();
    return 0;
}