2017.7.4 ACM校内赛 Round 2
Problem A B-number
题目大意 求1到n中包含连续子串"13"的数且能被13整除的数有多少个。
->题目传送站[here]
不难想到数位dp，现在开始设计状态。包含子串"13"可以用0， 1， 2来标记，如果从高位到低位dp的话，意义见下表。
| Status | Meaning |
|---|---|
| 0 | 子串"13"从未出现过 |
| 1 | 子串"13"从未出现过，但字符'1'出现在已经确定的部分的最右侧 |
| 2 | 子串"13"已经出现过了 |
对于能被13整除的数也很好处理，直接加一个状态记录此数除以13的余数。
然后数位dp两种实现方法:1.先用一次dp预处理出一个数组，然后根据某些套路进行计算。2.每次用记忆化搜索去做。
方法1我在比赛的时候没写出来，下来没调出来，直接重写，用方法2。值得注意一点就是使用dp值和记录dp值的前提是没有卡着"上界"。
Code
1 /** 2 * hdu 3652 - A 3 * Accepted 4 * author:yyf 5 * Time:16ms 6 * Memory:1876k 7 */ 8 #include <cstdio> 9 #include <cstdlib> 10 #include <cstring> 11 #include <ctime> 12 #include <cmath> 13 #include <cctype> 14 #include <iostream> 15 #include <fstream> 16 #include <sstream> 17 #include <algorithm> 18 #include <set> 19 #include <stack> 20 #include <vector> 21 #include <map> 22 #include <queue> 23 #include <list> 24 #ifdef WIN32 25 #define Auto "%I64d" 26 #else 27 #define Auto "%lld" 28 #endif 29 using namespace std; 30 typedef bool boolean; 31 #define smax(a, b) a = max(a, b) 32 #define smin(a, b) a = min(a, b); 33 const signed int inf = (signed)((1u << 31) - 1); 34 35 int n; 36 int digit[10]; 37 int power[10]; 38 char buf[100]; 39 int f[11][15][3]; 40 /** 41 *@param status 1 - "13" haven't appeared yet, 2 - "13" haven't appeared yet, but digit '1' at the right of the number has been OK, 3 - "13" has appeared. 42 */ 43 int dfs(int pos, int rest, int status, boolean betop) { //Digits dp 44 if(pos == -1) 45 return (rest == 0 && status == 2) ? (1) : (0); 46 if(!betop && f[pos][rest][status] != -1) 47 return f[pos][rest][status]; 48 49 int ret = 0; 50 int nstatus; 51 boolean nbetop; 52 int lim = (betop) ? (digit[pos]) : (9); 53 for(int i = 0; i <= lim; i++) { 54 nstatus = 0; 55 if(status == 2) 56 nstatus = 2; 57 if(status == 1) 58 nstatus = (i == 3) ? (2) : (0); 59 if(nstatus == 0) 60 nstatus = (i == 1) ? (1) : (0); 61 ret += dfs(pos - 1, (rest * 10 + i) % 13, nstatus, betop && i == lim); 62 } 63 if(!betop) 64 f[pos][rest][status] = ret; 65 66 return ret; 67 } 68 69 inline void init() { 70 memset(f, -1, sizeof(f)); 71 power[0] = 1; 72 for(int i = 1; i < 10; i++) 73 power[i] = power[i - 1] * 10; 74 } 75 76 inline void solve() { 77 while(~scanf("%d", &n)) { 78 // memset(f, -1, sizeof(f)); 79 int x = n, len = 0; 80 while(x) digit[len++] = x % 10, x /= 10; 81 // reverse(digit, digit + len); 82 printf("%d\n", dfs(len - 1, 0, 0, true)); 83 } 84 } 85 86 int main() { 87 init(); 88 solve(); 89 return 0; 90 }
Problem B The Captain
题目大意 定义直角坐标系内任意两点间行走的费用是这两点横纵坐标之差的绝对值的最小值。求点1到点n的最小费用。
->题目传送站[here]
我开始以为是dp加什么鬼畜的堆优化，优化到O(nlogn)，然而答案是图论大水题。。。
考虑3个点，设它们的坐标分别为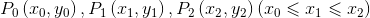
,设两点X, Y间的最小费用为f(X, Y)，则不难得到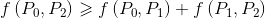
。对于当y满足这个关系时，也可以得到相似的结论。同时这个也可以推广到点数更多的时候。
因此建图时只需按横纵坐标排序，将相邻的点连边。不过据说要卡不加任何优化的spfa。。（虽然贴的是队友的代码，感觉不太好，但还是这么愉快地贴了）
Code
1 /** 2 * bzoj 4152 - B 3 * Accepted 4 * Author:lemonoil 5 */ 6 #include <cstdio> 7 #include <cstdlib> 8 #include <cstring> 9 #include <ctime> 10 #include <cmath> 11 #include <cctype> 12 #include <iostream> 13 #include <fstream> 14 #include <sstream> 15 #include <algorithm> 16 #include <set> 17 #include <stack> 18 #include <vector> 19 #include <map> 20 #include <queue> 21 #include <list> 22 using namespace std; 23 const int N = 200005; 24 const int inf = 2100000000; 25 int n,k; 26 int xx[N],yy[N],d[N],tot,head[N]; 27 struct edge{ 28 int to,w,next; 29 }e[N<<2]; 30 struct data{ 31 int x,y; 32 void read(){ 33 scanf("%d%d",&x,&y); 34 } 35 }a[N<<2]; 36 int cmpx(const int i,const int j){ 37 return a[i].x<a[j].x; 38 } 39 int cmpy(const int i,const int j){ 40 return a[i].y<a[j].y; 41 } 42 void addege(int x,int y,int z){ 43 e[++tot].next=head[x];e[tot].to=y;e[tot].w=z;head[x]=tot; 44 } 45 void add(int x,int y,int z){ 46 addege(x,y,z);addege(y,x,z); 47 } 48 struct node{ 49 int x,d; 50 bool operator < (const node & rhs)const{ 51 return d>rhs.d; 52 } 53 node(){} 54 node(int x,int d):x(x),d(d){} 55 }; 56 priority_queue<node> Q; 57 void dijk(){ 58 for(int i=0;i<=n;i++)d[i]=inf; 59 Q.push(node(0,0));d[0]=0; 60 while(!Q.empty()){ 61 node t=Q.top();Q.pop(); 62 if(d[t.x]!=t.d)continue; 63 for(int i=head[t.x];i;i=e[i].next){ 64 if(d[e[i].to]>d[t.x]+e[i].w){ 65 d[e[i].to]=d[t.x]+e[i].w; 66 Q.push(node(e[i].to,d[e[i].to])); 67 } 68 } 69 } 70 } 71 int main(){ 72 scanf("%d",&n); 73 for(int i=0;i<n;i++){ 74 a[i].read(); 75 xx[i]=yy[i]=i; 76 } 77 sort(xx,xx+n,cmpx); 78 for(int i=0;i<n-1;i++){ 79 data *x=a+xx[i],*y=a+xx[i+1]; 80 if((y->x-x->x)<=abs(x->y-y->y)){ 81 add(xx[i],xx[i+1],(y->x - x->x)); 82 } 83 } 84 sort(yy,yy+n,cmpy); 85 for(int i=0;i<n-1;i++){ 86 data *x=a+yy[i],*y=a+yy[i+1]; 87 if((y->y-x->y)<=abs(x->x-y->x)){ 88 add(yy[i],yy[i+1],y->y - x->y); 89 } 90 } 91 dijk(); 92 printf("%d\n",d[n-1]); 93 return 0; 94 }
Problem C 聪明的猴子
题目大意 在森林里有m只猴子和n棵树，给出每棵树的坐标和每只猴子的最远跳跃距离，问有多少只猴子能够直接或间接到达所有树。
->题目传送站[here]
最小生成树，不解释这些。
1 /** 2 * bzoj 2429 - C 3 * Accepted 4 * Author:Maverick 5 */ 6 #include <cstdio> 7 #include <cstdlib> 8 #include <cstring> 9 #include <ctime> 10 #include <cmath> 11 #include <cctype> 12 #include <iostream> 13 #include <fstream> 14 #include <sstream> 15 #include <algorithm> 16 #include <set> 17 #include <stack> 18 #include <vector> 19 #include <map> 20 #include <queue> 21 #include <list> 22 23 using namespace std; 24 25 const int maxn = 1005; 26 const int maxm = 505; 27 int n,m,tot,fin,ans; 28 int jp[maxm],x[maxn],y[maxn]; 29 struct Edge { 30 int frm,to; 31 double len; 32 bool operator < (const Edge & a) const { 33 if(len != a.len) return len < a.len; 34 if(frm != a.frm) return frm < a.frm; 35 return to < a.to; 36 } 37 } e[maxn*maxn]; 38 int fa[maxn*maxn]; 39 40 void addedge(int frm, int to) { 41 e[++tot].frm = frm; 42 e[tot].to = to; 43 int len = (x[frm]-x[to])*(x[frm]-x[to])+(y[frm]-y[to])*(y[frm]-y[to]); 44 e[tot].len = sqrt(len); 45 } 46 47 int find(int frm) { 48 if(frm == fa[frm]) return frm; 49 return fa[frm] = find(fa[frm]); 50 } 51 52 void unionn(int frm, int to) { 53 if(find(frm) != find(to)) fa[find(to)] = find(frm); 54 } 55 56 int main () { 57 scanf("%d",&m); 58 for(int i = 1; i <= m; i++) scanf("%d",&jp[i]); 59 scanf("%d",&n); 60 for(int i = 1; i <= n; i++) scanf("%d%d",&x[i],&y[i]); 61 for(int i = 1; i <= n; i++) 62 for(int j = 1; j <= n; j++) 63 if(i != j) addedge(i, j); 64 sort(e+1, e+1+tot); 65 for(int i = 1; i <= n*n; i++) fa[i] = i; 66 for(int i = 1; i <= tot; i++) { 67 if(find(e[i].to) != find(e[i].frm)) unionn(e[i].to, e[i].frm), fin++; 68 if(fin == n-1) { ans = e[i].len; break; } 69 } 70 int cnt = 0; 71 for(int i = 1; i <= m ; i++) if(jp[i] >= ans) cnt++; 72 printf("%d\n",cnt); 73 return 0; 74 }
Problem D 互不侵犯King
题目大意 国王会攻击它周围的8个方框内的其他棋子，求在一个n * n的棋盘内放k个国王使得它们不互相攻击的方案数。
->题目传送站[here]
由于n很小，很容易想到状压dp(其实我队友想爆搜),我开始试图用轮廓线，毕竟棋盘形，设计了状态，发现会T掉，重新设计了状态，应该可以AC，不想写直接扔给队友(我怀疑我是来坑队友的)，队友很强用朴素状压dp把它水掉。
思路是用f[i][s][k]表示第i行，放国王的位子(有国王的位子为1，没有国王的位子为0)，已经选了k个国王的方案数，转移时暴力枚举旧状态和新状态，再判断是否合法。但是这样会TLE，所以队友提前暴力预处理转移表，合法为true，不合法为false，就可以实现O(1)转移了。主dp过程就四层for大暴力就好了。
Code
1 /** 2 * bzoj 1087 - D 3 * Accepted 4 * author:lemonoil 5 */ 6 #include<iostream> 7 #include<cstdio> 8 using namespace std; 9 int n,m,tot,sum[512]; 10 long long f[10][100][512]; 11 int p[512],g[512][512]; 12 long long ans,s; 13 inline void read(int &res){ 14 static char ch;int flag=1; 15 while((ch=getchar())<'0'||ch>'9')if(ch=='-')flag=-1;res=ch-48; 16 while((ch=getchar())>='0'&&ch<='9')res=res*10+ch-48;res*=flag; 17 } 18 void init(){ 19 for(register int i=0;i<=tot;i++) 20 if((i&(i>>1))==0){s=0; 21 for(register int x=i;x;x>>=1)s+=(x&1); 22 sum[i]=s,p[i]=1; 23 } 24 for(register int i=0;i<=tot;i++)if(p[i]) 25 for(register int j=0;j<=tot;j++)if(p[j]) 26 if(((i&j)==0)&&((i&(j>>1))==0)&&((j&(i>>1))==0))g[i][j]=1; 27 } 28 int main(){ 29 read(n),read(m); 30 tot=(1<<n)-1;init(); 31 for(register int i=0;i<=tot;i++)if(p[i])f[1][sum[i]][i]=1; 32 for(register int j=1;j<n;j++) 33 for(register int k=0;k<=tot;k++)if(p[k]) 34 for(register int i=0;i<=tot;i++)if(p[i])if(g[k][i]) 35 for(register int p=sum[k];p+sum[i]<=m;p++) 36 f[j+1][p+sum[i]][i]+=f[j][p][k]; 37 for(register int i=0;i<=tot;i++)ans+=f[n][m][i]; 38 printf("%lld\n",ans); 39 return 0; 40 }
Problem E 管道取珠
(不会概述题目,请自行戳这里查看原题)
看到这道题，我一直在想组合数乱搞。。后来发现正确理解a^2的意义后，变成了一道dp水题，但仍然全场无队AC.。。
大神们将平方理解成两个进行相同的游戏，最后得到相同的序列的方案数。于是用f[i][j][k]表示总共取了i个球，第一个人在上面取了j个球，第二个人在下面取了k个球。转移是显然的，不清楚可以看代码。
Code
1 /** 2 * bzoj 1566 - E 3 * Accepted 4 * author:yyf 5 * Time:9292ms 6 * Memory:3280k 7 */ 8 #include <cstdio> 9 #include <cstdlib> 10 #include <cstring> 11 #include <ctime> 12 #include <cmath> 13 #include <cctype> 14 #include <iostream> 15 #include <fstream> 16 #include <sstream> 17 #include <algorithm> 18 #include <set> 19 #include <stack> 20 #include <vector> 21 #include <map> 22 #include <queue> 23 #include <list> 24 #ifdef WIN32 25 #define Auto "%I64d" 26 #else 27 #define Auto "%lld" 28 #endif 29 using namespace std; 30 typedef bool boolean; 31 #define smax(a, b) a = max(a, b) 32 #define smin(a, b) a = min(a, b); 33 const signed int inf = (signed)((1u << 31) - 1); 34 35 const int moder = 1024523; 36 37 inline int mod_plus(int a, int b) { 38 int ret = a + b; 39 while(ret >= moder) ret -= moder; 40 return ret; 41 } 42 43 #define smod_plus(a, b) a = mod_plus(a, b) 44 45 int n, m; 46 char a[505]; 47 char b[505]; 48 int f[2][505][505]; 49 50 inline void init() { 51 scanf("%d%d%s%s", &n, &m, a, b); 52 } 53 54 inline void solve() { 55 int t = 0; 56 f[t][0][0] = 1; 57 for(int i = 0; i < n + m; i++) { 58 t ^= 1; 59 memset(f[t], 0, sizeof(f[t])); 60 for(int j = 0; j <= n && j <= i; j++) { 61 for(int k = 0; k <= n && k <= i; k++) { 62 int x = i - j, y = i - k; 63 if(j < n && k < n && a[j] == a[k]) 64 smod_plus(f[t][j + 1][k + 1], f[t ^ 1][j][k]); 65 if(x < m && k < n && b[x] == a[k]) 66 smod_plus(f[t][j][k + 1], f[t ^ 1][j][k]); 67 if(j < n && y < m && a[j] == b[y]) 68 smod_plus(f[t][j + 1][k], f[t ^ 1][j][k]); 69 if(x < m && y < m && b[x] == b[y]) 70 smod_plus(f[t][j][k], f[t ^ 1][j][k]); 71 } 72 } 73 } 74 printf("%d\n", f[t][n][n]); 75 } 76 77 int main() { 78 init(); 79 solve(); 80 return 0; 81 }
Problem F 树上操作
(题目太裸,请自行戳这里查看原题)
树链剖分不解释，如果不会可以看这篇博客[here]
由于比赛时怕写得很长(大概也就200行左右吧。。)，半天调不出来，果断让给队友。
Code
1 /** 2 * bzoj 4034 - F 3 * Accepted 4 * author:lemonoil 5 */ 6 #include <cstdio> 7 #include <cstdlib> 8 #include <cstring> 9 #include <ctime> 10 #include <cmath> 11 #include <cctype> 12 #include <iostream> 13 #include <fstream> 14 #include <sstream> 15 #include <algorithm> 16 #include <set> 17 #include <stack> 18 #include <vector> 19 #include <map> 20 #include <queue> 21 #include <list> 22 using namespace std; 23 typedef bool boolean; 24 typedef long long ll; 25 #define smax(a, b) a = max(a, b) 26 #define smin(a, b) a = min(a, b) 27 #define R(rt) rt<<1|1 28 #define L(rt) rt<<1 29 const int N=300005; 30 using namespace std; 31 int tot,n,m,next[N],point[N],v[N],deep[N],fa[N],size[N],son[N]; 32 ll tr[N*4],delta[N*4]; 33 int val[N],l[N],r[N],q[N],pos[N],cnt,belong[N]; 34 inline void add(int x,int y){ 35 next[++tot]=point[x]; point[x]=tot; v[tot]=y; 36 next[++tot]=point[y]; point[y]=tot; v[tot]=x; 37 } 38 inline void dfsf(int x,int f){ 39 deep[x]=deep[f]+1; 40 size[x]=1; 41 for(register int i=point[x];i;i=next[i]) 42 if(v[i]!=f){ 43 fa[v[i]]=x; 44 dfsf(v[i],x); 45 size[x]+=size[v[i]]; 46 if(size[son[x]]<size[v[i]])son[x]=v[i]; 47 } 48 } 49 inline void dfsfs(int x,int chain){ 50 belong[x]=chain; pos[x]=++cnt; l[x]=r[x]=cnt; q[cnt]=x; 51 if(!son[x])return; 52 dfsfs(son[x],chain); 53 for(register int i=point[x];i;i=next[i]) 54 if(v[i]!=fa[x]&&v[i]!=son[x]) 55 dfsfs(v[i],v[i]); 56 r[x]=cnt; 57 } 58 inline void update(int rt){ 59 tr[rt]=tr[L(rt)]+tr[R(rt)]; 60 } 61 inline void build(int rt,int l,int r){ 62 if(l==r){ 63 tr[rt]=(ll)val[q[l]]; 64 return; 65 } 66 register int mid=(l+r)>>1; 67 build(L(rt),l,mid); 68 build(R(rt),mid+1,r); 69 update(rt); 70 } 71 inline void pushdown(int rt,int l,int r){ 72 register int mid=(l+r)>>1; 73 if(delta[rt]){ 74 tr[L(rt)]+=(ll)(mid-l+1)*delta[rt]; 75 tr[R(rt)]+=(ll)(r-mid)*delta[rt]; 76 delta[L(rt)]+=delta[rt]; 77 delta[R(rt)]+=delta[rt]; 78 delta[rt]=0; 79 } 80 } 81 inline void update_point(int rt,int l,int r,int x,int v){ 82 if(l==r){ 83 tr[rt]+=(ll)v; 84 return; 85 } 86 register int mid=(l+r)>>1; 87 pushdown(rt,l,r); 88 if(x<=mid)update_point(L(rt),l,mid,x,v); 89 else update_point(R(rt),mid+1,r,x,v); 90 update(rt); 91 } 92 inline void change(int rt,int l,int r,int ll,int rr,int v){ 93 if(ll<=l&&r<=rr){ 94 tr[rt]+=(long long)v*(long long)(r-l+1); 95 delta[rt]+=(long long)v; 96 return; 97 } 98 register int mid=(l+r)>>1; 99 pushdown(rt,l,r); 100 if(ll<=mid)change(L(rt),l,mid,ll,rr,v); 101 if(rr>mid)change(R(rt),mid+1,r,ll,rr,v); 102 update(rt); 103 } 104 inline long long query_sum(int rt,int l,int r,int ll,int rr){ 105 if(ll<=l&&r<=rr)return tr[rt]; 106 int mid=(l+r)/2; 107 register long long ans=0; 108 pushdown(rt,l,r); 109 if(ll<=mid)ans+=query_sum(L(rt),l,mid,ll,rr); 110 if(rr>mid)ans+=query_sum(R(rt),mid+1,r,ll,rr); 111 return ans; 112 } 113 inline long long solve(int x,int y){ 114 ll ans=0; 115 while(belong[x]!=belong[y]){ 116 if(deep[belong[x]]<deep[belong[y]])swap(x,y); 117 ans+=query_sum(1,1,n,pos[belong[x]],pos[x]); 118 x=fa[belong[x]]; 119 } 120 if(deep[x]>deep[y])swap(x,y); 121 ans+=query_sum(1,1,n,pos[x],pos[y]); 122 return ans; 123 } 124 inline void read(int &res){ 125 static char ch;int flag=1; 126 while((ch=getchar())<'0'||ch>'9')if(ch=='-')flag=-1;res=ch-48; 127 while((ch=getchar())>='0'&&ch<='9')res=res*10+ch-48;res*=flag; 128 } 129 int main(){ 130 read(n),read(m); 131 for(register int i=1;i<=n;i++)read(val[i]); 132 for(register int i=1;i<n;i++){ 133 register int x,y; read(x),read(y); 134 add(x,y); 135 } 136 dfsf(1,0); dfsfs(1,1); 137 build(1,1,n); 138 for(register int i=1;i<=m;i++){ 139 int opt,x,y;read(opt); 140 if(opt==1){ 141 read(x),read(y); 142 update_point(1,1,n,pos[x],y); 143 }if(opt==2){ 144 read(x),read(y); 145 change(1,1,n,l[x],r[x],y); 146 }if(opt==3){ 147 read(x); 148 printf("%I64d\n",solve(1,x)); 149 } 150 } 151 }
Problem G 覆盖问题
题目大意 给定平面上n个点，求用3个完全相同正方形邻边分明平行x轴和y轴覆盖n个点(包括边界)，的最小边长。
黄学长O(n)贪心膜拜一发。
现在开始扯您能听懂的方法。
不难想到二分答案。关键在于check。考虑用一个巨大的矩形刚好框住这些点(如果不清楚就看看下图)。
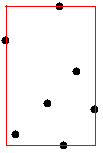
因为每条边上都有1个点，因此可以得出结论至少有一个矩形覆盖了这个矩形的一个顶点(当矩形数变成4时不一定成立)。所以可以枚举用正方形覆盖哪一个角落然后打上标记，递归处理，再判下边界判断即可。还是比较好写。
Code
1 /** 2 * bzoj 1052 - G 3 * Accepted 4 * Author:yyf 5 * Time:268ms 6 * Memory:1448k 7 */ 8 #include <cstdio> 9 #include <cstdlib> 10 #include <cstring> 11 #include <ctime> 12 #include <cmath> 13 #include <cctype> 14 #include <iostream> 15 #include <fstream> 16 #include <sstream> 17 #include <algorithm> 18 #include <set> 19 #include <stack> 20 #include <vector> 21 #include <map> 22 #include <queue> 23 #include <list> 24 #ifdef WIN32 25 #define Auto "%I64d" 26 #else 27 #define Auto "%lld" 28 #endif 29 using namespace std; 30 typedef bool boolean; 31 #define smax(a, b) a = max(a, b) 32 #define smin(a, b) a = min(a, b); 33 const signed int inf = (signed)((1u << 31) - 1); 34 const double eps = 1e-10; 35 36 typedef class Point { 37 public: 38 int x; 39 int y; 40 Point(int x = 0, int y = 0):x(x), y(y) { } 41 }Point; 42 43 int n; 44 Point *ps; 45 46 inline void init() { 47 scanf("%d", &n); 48 ps = new Point[n]; 49 for(int i = 0; i < n; i++) 50 scanf("%d%d", &ps[i].x, &ps[i].y); 51 } 52 53 inline boolean inside(Point p, Point r, int wid, int hei) { 54 return p.x >= r.x && p.x <= (r.x + wid) && p.y >= r.y && p.y <= (r.y + hei); 55 } 56 57 int cover; 58 int *cov; 59 boolean dfs(int dep, int L) { 60 int maxx = 0, maxy = 0, minx = inf, miny = inf; 61 for(int i = 0; i < n; i++) { 62 if(cov[i] != -1) continue; 63 smax(maxx, ps[i].x); 64 smin(minx, ps[i].x); 65 smax(maxy, ps[i].y); 66 smin(miny, ps[i].y); 67 } 68 69 if(dep == 2) { 70 return maxx - minx <= L && maxy - miny <= L; 71 } 72 73 Point br[4] = {Point(minx, miny), Point(minx, maxy - L), Point(maxx - L, miny), Point(maxx - L, maxy - L)}; 74 for(int k = 0; k < 4; k++) { 75 int cnt = 0; 76 for(int i = 0; i < n; i++) 77 if(cov[i] == -1 && inside(ps[i], br[k], L, L)) 78 cov[i] = dep, cnt++; 79 cover += cnt; 80 if(dfs(dep + 1, L)) return true; 81 cover -= cnt; 82 for(int i = 0; i < n; i++) 83 if(cov[i] == dep) 84 cov[i] = -1; 85 } 86 return false; 87 } 88 89 boolean check(int mid) { 90 cover = 0; 91 memset(cov, -1, sizeof(int) * n); 92 return dfs(0, mid); 93 } 94 95 inline void solve() { 96 cov = new int[n]; 97 int l = 0, r = 1e8; 98 while(l <= r) { 99 int mid = (int)((l * 1LL + r) >> 1); 100 if(check(mid)) r = mid - 1; 101 else l = mid + 1; 102 } 103 printf("%d\n", r + 1); 104 } 105 106 int main() { 107 init(); 108 solve(); 109 return 0; 110 }
Problem H 楼房重建
题目大意 平面上有些线段，一段在y轴且平行于x，另一端在第一象限。有一些修改操作，修改线段的长度，每次修改完询问平面内有多少条线段再第一象限内的端点和原点的连线不与其他线段相交(包括端点)。
->题目传送站[here]
我开始看这道题的时候想到了分块，然后队友立刻否决我的想法。然后比赛结束后，光速被打脸了。。
首先简化一下问题吧。不与其他线段相交的条件是在第一象限内的端点与原点连线的斜率严格大于之前的连线的斜率。求的是"连续"严格上升子序列(请区别于LIS)。为了更好说明所说的这个序列指何物:
原序列 1 4 2 7 3 9 4 5 6
LIS可以是： 1 2 4 5 6
但我所说的序列是：1 4 7 9
先说分块做法吧，按照常规，每块大小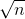
个元素，记录对应位置的连线的斜率和当前块的这样的上升序列。修改操作直接暴力重构整个块的序列。时间复杂度
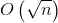。对于查询操作就从第一个块开始遍历，记录当前找到的最大的斜率，在下一个中进行upper_bound（二分快速找到合法的第一个），更新答案，时间复杂度$O(\sqrt{n} \log n)$。所以总时间复杂度$O(n\sqrt{n} \log n)$，还是可以卡过去的(毕竟时限这么宽松嘛)。
Code
1 /** 2 * bzoj 2957 - H 3 * Accepted 4 * author:yyf 5 * Time:5528ms 6 * Memory:3312k 7 */ 8 #include <cstdio> 9 #include <cstdlib> 10 #include <cstring> 11 #include <ctime> 12 #include <cmath> 13 #include <cctype> 14 #include <iostream> 15 #include <fstream> 16 #include <sstream> 17 #include <algorithm> 18 #include <set> 19 #include <stack> 20 #include <vector> 21 #include <map> 22 #include <queue> 23 #include <list> 24 #ifdef WIN32 25 #define Auto "%I64d" 26 #else 27 #define Auto "%lld" 28 #endif 29 using namespace std; 30 typedef bool boolean; 31 #define smax(a, b) a = max(a, b) 32 #define smin(a, b) a = min(a, b); 33 const signed int inf = (signed)((1u << 31) - 1); 34 const double eps = 1e-10; 35 36 typedef class Chunk { // Blocks 37 public: 38 int size; // The size of the chunk. 39 int slis; 40 double arr[400]; 41 double lis[400]; 42 43 Chunk():size(0), slis(0) { } 44 Chunk(int s):size(s), slis(0) { } 45 46 void rebuild() { 47 slis = 0; 48 double temp = 0; 49 for(int i = 0; i < size; i++) 50 if(arr[i] > temp + eps) 51 temp = arr[i], lis[slis++] = temp; 52 } 53 54 int upper_bound(double x) { 55 return std::upper_bound(lis, lis + slis, x) - lis; 56 } 57 }Chunk; 58 59 int n, m; 60 int csize; 61 int cc = 0; 62 Chunk* cs; 63 64 inline void init() { 65 scanf("%d%d", &n, &m); 66 csize = (int)sqrt(n + 0.5); 67 cs = new Chunk[csize + 5]; 68 for(; cc * csize <= n; cc++) { 69 cs[cc].size = csize; 70 for(int i = 0; i < csize; i++) { 71 cs[cc].arr[i] = 0; 72 } 73 } 74 } 75 76 inline void solve() { 77 int pos, h; 78 while(m--) { 79 scanf("%d%d", &pos, &h); 80 int id = pos / csize; 81 cs[id].arr[pos % csize] = h * 1.0 / pos; 82 cs[id].rebuild(); 83 double temp = 0; 84 int res = 0; 85 for(int i = 0; i < cc; i++) { 86 int p = cs[i].upper_bound(temp); 87 if(p < cs[i].slis) { 88 res += cs[i].slis - p; 89 temp = cs[i].lis[cs[i].slis - 1]; 90 } 91 } 92 printf("%d\n", res); 93 } 94 } 95 96 int main() { 97 init(); 98 solve(); 99 return 0; 100 }
还有一种做法是用线段树。
不用废话的是需要记录在当前一段内斜率递增的序列的长度。为了更好地维护还需要记录最大的斜率。
维护时当区间的最大斜率小于等于要求的最小斜率时直接记0。
如果左边的最大息率小于等于要求的最小斜率时，对答案的贡献为0，用这个方法递归处理右边。
否则右边是可以计算出来的，因为右边看得到的建筑还是看得到，看不到的，还是看不到，因此就是val - l->val。所以用这个方法递归处理左边。
然后判判边界就好了。
因为每次递归的子问题大小都为原问题的一半，所以维护的时间复杂度为$O(\log n)$，因此总时间复杂度为$O(n\log^2 n)$.
最后想吐槽一下这道题，建筑队脑子可能是有问题吧，还要不要别人住房子啊？
Code
1 /** 2 * bzoj 2957 - H 3 * Accepted 4 * author:yyf 5 * Time:1484ms 6 * Memory:9108k 7 */ 8 #include <cstdio> 9 #include <cstdlib> 10 #include <cstring> 11 #include <ctime> 12 #include <cmath> 13 #include <cctype> 14 #include <iostream> 15 #include <fstream> 16 #include <sstream> 17 #include <algorithm> 18 #include <set> 19 #include <stack> 20 #include <vector> 21 #include <map> 22 #include <queue> 23 #include <list> 24 #ifdef WIN32 25 #define Auto "%I64d" 26 #else 27 #define Auto "%lld" 28 #endif 29 using namespace std; 30 typedef bool boolean; 31 #define smax(a, b) a = max(a, b) 32 #define smin(a, b) a = min(a, b); 33 const signed int inf = (signed)((1u << 31) - 1); 34 const double eps = 1e-10; 35 36 typedef class SegTreeNode { 37 public: 38 SegTreeNode *l, *r; 39 int len; 40 double val; 41 42 SegTreeNode():l(NULL), r(NULL), len(0), val(0.0) { } 43 44 int count(double low) { 45 if(!l) return (val > low) ? (1) : (0); 46 if(val <= low) return 0; 47 if(l->val <= low) return r->count(low); 48 return l->count(low) + len - l->len; 49 } 50 51 void pushUp() { 52 val = max(l->val, r->val); 53 len = l->len + r->count(l->val); 54 } 55 }SegTreeNode; 56 57 typedef class SegTree { 58 public: 59 SegTreeNode* pool; 60 SegTreeNode* tail; 61 62 SegTreeNode* root; 63 64 SegTree():root(NULL) { } 65 SegTree(int n) { 66 pool = new SegTreeNode[(n << 2)]; 67 tail = pool; 68 build(root, 1, n); 69 } 70 71 SegTreeNode* newnode() { 72 return tail++; 73 } 74 75 void build(SegTreeNode*& node, int l, int r) { 76 node = newnode(); 77 if(l == r) return; 78 int mid = (l + r) >> 1; 79 build(node->l, l, mid); 80 build(node->r, mid + 1, r); 81 } 82 83 void update(SegTreeNode*& node, int l, int r, int idx, double s) { 84 if(l == r) { 85 node->val = s; 86 node->len = 1; 87 return; 88 } 89 int mid = (l + r) >> 1; 90 if(idx <= mid) update(node->l, l, mid, idx, s); 91 else update(node->r, mid + 1, r, idx, s); 92 node->pushUp(); 93 } 94 95 int query() { 96 return root->len; 97 } 98 }SegTree; 99 100 int n, m; 101 SegTree st; 102 103 inline void init() { 104 scanf("%d%d", &n, &m); 105 st = SegTree(n); 106 } 107 108 inline void solve() { 109 int pos, h; 110 double slope; 111 while(m--) { 112 scanf("%d%d", &pos, &h); 113 slope = h * 1.0 / pos; 114 st.update(st.root, 1, n, pos, slope); 115 printf("%d\n", st.query()); 116 } 117 } 118 119 int main() { 120 init(); 121 solve(); 122 return 0; 123 }
Problem I 谁能赢呢？
题目大意 在一个n * n的棋盘的最左上角有一个棋子，两个人轮流移动这个棋子，每次只能向上下左右四个方向移动一格，不能走重复的路，不能移出边界，谁先不能移动谁就输，如果两人采取最优的策略，问最后谁会赢。
->题目传送站[here]
没有保持R1的传统，直接第一个A掉最水的一道题。(我们教练期望我们在15分钟内A掉这道题)。
不说过多的废话，题解就是如果n是偶数先手必胜，否则先手必败。
至于证明，我看到的有一种说法就是将先手和后手连续的一步看成一个1×2的多米诺骨牌。当n为偶数时，少了左上角的一块后，不存在完美覆盖，所以此时先手必胜。n为奇数时少了左上角的一块后，存在完美覆盖，所以先手必败。
Code
1 /** 2 * bzoj 2463 - I 3 * Accepted 4 * author:yyf 5 */ 6 #include <iostream> 7 using namespace std; 8 9 int main() { 10 int n; 11 while(cin >> n) { 12 if(n == 0) break; 13 if(n & 1) cout << "Bob" << endl; 14 else cout << "Alice" << endl; 15 } 16 return 0; 17 }
Problem J 仪仗队
题目大意 求横纵坐标都为整数，且都小于n ，并且互质的点有多少个。
->题目传送站[here]
由于我比较蠢，傻逼地用容斥。大佬们直接欧拉函数求phi(1) + ... + phi(n - 1)乘2再加1就是答案。。
Code
1 /** 2 * bzoj 2190 - J 3 * Accepted 4 * author:yyf 5 */ 6 #include <cstdio> 7 #include <cstdlib> 8 #include <cstring> 9 #include <ctime> 10 #include <cmath> 11 #include <cctype> 12 #include <iostream> 13 #include <fstream> 14 #include <sstream> 15 #include <algorithm> 16 #include <set> 17 #include <stack> 18 #include <vector> 19 #include <map> 20 #include <queue> 21 #include <list> 22 #ifdef WIN32 23 #define Auto "%I64d" 24 #else 25 #define Auto "%lld" 26 #endif 27 using namespace std; 28 typedef bool boolean; 29 #define smax(a, b) a = max(a, b) 30 #define smin(a, b) a = min(a, b); 31 const signed int inf = (signed)((1u << 31) - 1); 32 33 int n; 34 35 inline void init() { 36 scanf("%d", &n); 37 } 38 39 const int limit = 4e4; 40 int num = 0; 41 int pri[10000]; 42 boolean vis[40005]; 43 int phi[40005]; 44 45 inline void Euler() { 46 memset(vis, false, sizeof(vis)); 47 vis[1] = true, phi[1] = 1; 48 for(int i = 2; i <= limit; i++) { 49 if(!vis[i]) pri[num++] = i, phi[i] = i - 1; 50 for(int j = 0; j < num; j++) { 51 int x = i * pri[j]; 52 if(x > limit) break; 53 vis[x] = true; 54 if((i % pri[j]) == 0) { 55 phi[x] = phi[i] * pri[j]; 56 break; 57 } 58 phi[x] = phi[i] * (pri[j] - 1); 59 } 60 } 61 } 62 63 int num1; 64 int fac[10005]; 65 void getFactory(int a) { 66 num1 = 0; 67 for(int i = 0; pri[i] * pri[i] <= a; i++) { 68 if((a % pri[i]) == 0) { 69 fac[num1++] = pri[i]; 70 while((a % pri[i]) == 0) a /= pri[i]; 71 } 72 } 73 if(a != 1) fac[num1++] = a; 74 } 75 76 int getHz(int a, int moder) { 77 getFactory(moder); 78 int ret = 0; 79 for(int i = 1; i < (1 << num1); i++) { 80 int temp = 1, j = 0, aFlag = -1, x = i; 81 while(x) { 82 if(x & 1) temp *= fac[j], aFlag *= -1; 83 x >>= 1, j++; 84 } 85 ret += a / temp * aFlag; 86 } 87 return a - ret; 88 } 89 90 long long res = 2; 91 inline void solve() { 92 res += (n - 1); 93 int les = n - 1; 94 for(int i = 2; i < n; i++) { 95 // cout << res << endl; 96 res += getHz(les, i); 97 } 98 printf(Auto"\n", res); 99 } 100 101 int main() { 102 init(); 103 Euler(); 104 solve(); 105 return 0; 106 }
