poj 3667 Hotel - 线段树
The cows are journeying north to Thunder Bay in Canada to gain cultural enrichment and enjoy a vacation on the sunny shores of Lake Superior. Bessie, ever the competent travel agent, has named the Bullmoose Hotel on famed Cumberland Street as their vacation residence. This immense hotel has N (1 ≤ N ≤ 50,000) rooms all located on the same side of an extremely long hallway (all the better to see the lake, of course).
The cows and other visitors arrive in groups of size Di (1 ≤ Di ≤ N) and approach the front desk to check in. Each group i requests a set of Di contiguous rooms from Canmuu, the moose staffing the counter. He assigns them some set of consecutive room numbers r..r+Di-1 if they are available or, if no contiguous set of rooms is available, politely suggests alternate lodging. Canmuu always chooses the value of rto be the smallest possible.
Visitors also depart the hotel from groups of contiguous rooms. Checkout i has the parameters Xi and Di which specify the vacating of rooms Xi ..Xi +Di-1 (1 ≤ Xi ≤ N-Di+1). Some (or all) of those rooms might be empty before the checkout.
Your job is to assist Canmuu by processing M (1 ≤ M < 50,000) checkin/checkout requests. The hotel is initially unoccupied.
Input
* Line 1: Two space-separated integers: N and M
* Lines 2..M+1: Line i+1 contains request expressed as one of two possible formats: (a) Two space separated integers representing a check-in request: 1 and Di (b) Three space-separated integers representing a check-out: 2, Xi, and Di
Output
* Lines 1.....: For each check-in request, output a single line with a single integer r, the first room in the contiguous sequence of rooms to be occupied. If the request cannot be satisfied, output 0.
Sample Input
10 6 1 3 1 3 1 3 1 3 2 5 5 1 6
Sample Output
1 4 7 0 5
题意是说写一个数据结构,支持以下操作
1.Check-in 找一段连续的大小为k的空房间,使开始的位置尽量小
2.Check-out 使一段连续的房间变为空房间。
这里就直接讲正解了吧。用线段树,维护以下三个量
1.从最左边开始的一段连续的空房间的长度
2.从最右边开始的一段连续的空房间的长度
3.当前区间最长的一段连续的空房间长度
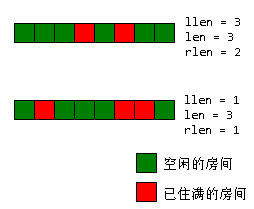
现在来思考一下维护,左边和右边连续比较简单,特殊处理当整个区间都是空闲的房间的情况。
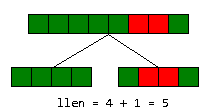
至于最长的连续的空闲房间呢,先用两段的len值更新它,然后再看一下中间合并后多出来的那一段是否可以更新len值。
Check-out操作现在可以完成了,和普通的线段树区间修改是一样的。
Check-in操作运用一点"人生的经验"(贪心),先看左边的len是否满足,满足的话就递归左边,再看中间是否满足,满足就返回结果(这个起点是可以算出来的),最后看右边是否满足。查询结束后,当结果不为0时才去把一段连续的空房间变为已住满的房间(我真的没有想出来边查询边打标记)。
Code
1 /** 2 * poj 3 * Problem#3667 4 * Accepted 5 * Time:1735ms 6 * Memory:5388k 7 */ 8 #include<iostream> 9 #include<fstream> 10 #include<sstream> 11 #include<algorithm> 12 #include<cstdio> 13 #include<cstring> 14 #include<cstdlib> 15 #include<cctype> 16 #include<cmath> 17 #include<ctime> 18 #include<map> 19 #include<stack> 20 #include<set> 21 #include<queue> 22 #include<vector> 23 #ifndef WIN32 24 #define AUTO "%lld" 25 #else 26 #define AUTO "%I64d" 27 #endif 28 using namespace std; 29 typedef bool boolean; 30 #define inf 0xfffffff 31 #define smin(a, b) (a) = min((a), (b)) 32 #define smax(a, b) (a) = max((a), (b)) 33 #define max3(a, b, c) max((a), max((b), (c))) 34 template<typename T> 35 inline boolean readInteger(T& u) { 36 char x; 37 int aFlag = 1; 38 while(!isdigit((x = getchar())) && x != '-' && x != -1); 39 if(x == -1) { 40 ungetc(x, stdin); 41 return false; 42 } 43 if(x == '-') { 44 aFlag = -1; 45 x = getchar(); 46 } 47 for(u = x - '0'; isdigit((x = getchar())); u = u * 10 + x - '0'); 48 u *= aFlag; 49 ungetc(x, stdin); 50 return true; 51 } 52 53 typedef class SegTreeNode { 54 public: 55 int len; 56 int llen; 57 int rlen; 58 int lazy; 59 SegTreeNode* left, *right; 60 SegTreeNode(const int len = 1, const int llen = 1, const int rlen = 1):len(len), llen(llen), rlen(rlen), lazy(0) { 61 left = right = NULL; 62 } 63 64 inline void pushUp(int l, int r, int mid) { 65 len = max3(left->len, right->len, left->rlen + right->llen); 66 llen = left->llen, rlen = right->rlen; 67 if(left->llen == (mid - l + 1)) llen = left->llen + right->llen; 68 if(right->rlen == (r - mid)) rlen = left->rlen + right->rlen; 69 } 70 71 inline void pushDown(int l, int r, int mid) { 72 this->left->len = this->left->llen = this->left->rlen = (lazy > 0) ? (mid - l + 1) : (0); 73 this->right->len= this->right->llen= this->right->rlen= (lazy > 0) ? (r - mid) : (0); 74 this->left->lazy = this->right->lazy = lazy; 75 lazy = 0; 76 } 77 }SegTreeNode; 78 79 typedef class SegTree { 80 public: 81 SegTreeNode *root; 82 83 SegTree():root(NULL) { } 84 SegTree(int s) { 85 build(root, 1, s); 86 } 87 88 void build(SegTreeNode*& node, int l, int r) { 89 node = new SegTreeNode(); 90 if(l == r) return; 91 int mid = (l + r) >> 1; 92 build(node->left, l, mid); 93 build(node->right, mid + 1, r); 94 node->pushUp(l, r, mid); 95 } 96 97 void update(SegTreeNode*& node, int l, int r, int cl, int cr, int val) { 98 int mid = (l + r) >> 1; 99 if(node->lazy && l != r) node->pushDown(l, r, mid); 100 if(cl == l && r == cr) { 101 node->lazy = (val) ? (1) : (-1); 102 node->len = node->llen = node->rlen = val * (r - l + 1); 103 return; 104 } 105 if(cr <= mid) update(node->left, l, mid, cl, cr, val); 106 else if(cl > mid) update(node->right, mid + 1, r, cl, cr, val); 107 else { 108 update(node->left, l, mid, cl, mid, val); 109 update(node->right, mid + 1, r, mid + 1, cr, val); 110 } 111 node->pushUp(l, r, mid); 112 } 113 114 int query(SegTreeNode*& node, int l, int r, int len) { 115 int mid = (l + r) >> 1; 116 if(node->lazy && l != r) node->pushDown(l, r, mid); 117 if(r - l + 1 == len) return l; 118 if(l == r) return 0; 119 if(node->left->len >= len) return query(node->left, l, mid, len); 120 else if(node->left->rlen + node->right->llen >= len && node->left->rlen > 0) 121 return mid - node->left->rlen + 1; 122 else if(node->right->len >= len) return query(node->right, mid + 1, r, len); 123 return 0; 124 } 125 126 }SegTree; 127 128 int n, m; 129 SegTree st; 130 131 inline void solve() { 132 readInteger(n); 133 readInteger(m); 134 st = SegTree(n); 135 for(int i = 1, a, b, c; i <= m; i++) { 136 readInteger(a); 137 readInteger(b); 138 if(a == 1) { 139 c = st.query(st.root, 1, n, b); 140 if(c != 0) st.update(st.root, 1, n, c, b + c - 1, 0); 141 printf("%d\n", c); 142 } else { 143 readInteger(c); 144 st.update(st.root, 1, n, b, b + c - 1, 1); 145 } 146 } 147 } 148 149 int main() { 150 solve(); 151 return 0; 152 }

 浙公网安备 33010602011771号
浙公网安备 33010602011771号