hdu 2256 Problem of Precision -矩阵快速幂

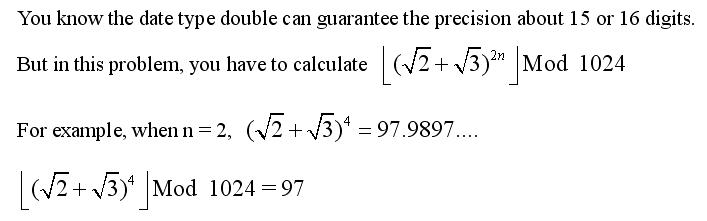
Input

　　The first line of input gives the number of cases, T. T test cases follow, each on a separate line. Each test case contains one positive integer n. (1 <= n <= 10^9) 
Output

　　For each input case, you should output the answer in one line. 
Sample Input

3
1
2
5

Sample Output

9
97
841

　　首先化简一下式子

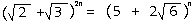
　　接着我们设

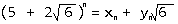
　　为了证明这个展开式一定是成立(n >= 1)，现在进行用归纳法证明

　　①当n = 1时，结论显然成立

　　②当n = k时，假设当n = k - 1时成立，那么有

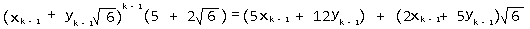
　　显然等号右边符合这个结构，由此结论成立。

　　同时，我们可以得出x和y的递推关系

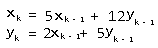
　　于是我们可以构造出矩阵，用来快速幂

 

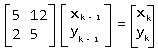
　　现在唯一的问题就是，怎么就这个式子的向下取整的值。正解一个很诡异的解法：

　　用类似的方法可以得出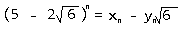

　　所以有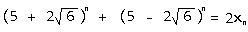

　　又因为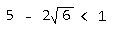

　　所以会小于1，

　　所以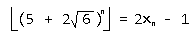

Code

  1 /**
  2  * hdu
  3  * Problem#2256
  4  * Accepted
  5  * Time:15ms
  6  * Memory:2920k
  7  */
  8 #include<iostream>
  9 #include<cstdio>
 10 #include<cctype>
 11 #include<cstring>
 12 #include<cstdlib>
 13 #include<fstream>
 14 #include<sstream>
 15 #include<algorithm>
 16 #include<map>
 17 #include<set>
 18 #include<queue>
 19 #include<vector>
 20 #include<stack>
 21 using namespace std;
 22 typedef bool boolean;
 23 #define INF 0xfffffff
 24 #define smin(a, b) a = min(a, b)
 25 #define smax(a, b) a = max(a, b)
 26 template<typename T>
 27 inline void readInteger(T& u){
 28     char x;
 29     int aFlag = 1;
 30     while(!isdigit((x = getchar())) && x != '-');
 31     if(x == '-'){
 32         x = getchar();
 33         aFlag = -1;
 34     }
 35     for(u = x - '0'; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - '0');
 36     ungetc(x, stdin);
 37     u *= aFlag;
 38 }
 39 
 40 #define moder 1024
 41 
 42 typedef class Matrix {
 43     public:
 44         int* p;
 45         int lines, cols;
 46         Matrix():p(NULL), lines(0), cols(0)    {    } 
 47         Matrix(int lines, int cols):lines(lines), cols(cols) {
 48             p = new int[(lines * cols)];
 49         }
 50         
 51         int* operator [](int pos) {
 52             return p + pos * cols;
 53         }
 54         
 55         Matrix operator * (Matrix b) {
 56             if(cols != b.lines)    return Matrix();
 57             Matrix res(lines, b.cols);
 58             for(int i = 0; i < lines; i++) {
 59                 for(int j = 0; j < b.cols; j++) {
 60                     res[i][j] = 0;
 61                     for(int k = 0; k < cols; k++) {
 62                         (res[i][j] += (*this)[i][k] * b[k][j] % moder) %= moder; 
 63                     } 
 64                 }
 65             }
 66             return res;
 67         }
 68 }Matrix;
 69 
 70 int n;
 71 Matrix I2;
 72 Matrix org;
 73 Matrix unit;
 74 
 75 template<typename T>
 76 T pow(T a, int pos) {
 77     if(pos == 0)    return I2;
 78     if(pos == 1)    return a;
 79     T temp = pow(a, pos / 2);
 80     if(pos & 1)    return temp * temp * a;
 81     return temp * temp; 
 82 }
 83 
 84 inline void init_matrix() {
 85     I2 = Matrix(2, 2);
 86     I2[0][0] = I2[1][1] = 1;
 87     I2[1][0] = I2[0][1] = 0;
 88     org = Matrix(2, 1);
 89     org[0][0] = 5, org[1][0] = 2;
 90     unit = Matrix(2, 2);
 91     unit[0][0] = 5, unit[0][1] = 12;
 92     unit[1][0] = 2, unit[1][1] = 5;
 93 }
 94 
 95 inline void init() {
 96     readInteger(n);
 97 }
 98 
 99 inline void solve() {
100     Matrix res = pow(unit, n - 1) * org;
101     printf("%d\n", (res[0][0] * 2 - 1) % moder);
102 }
103 
104 int T;
105 int main() {
106     readInteger(T);
107     init_matrix();
108     while(T--) {
109         init();
110         solve();
111     }
112     return 0;
113 }
posted @ 2017-03-18 20:11  阿波罗2003  阅读(144)  评论(0)  编辑  收藏  举报