bzoj 1096 仓库建设 -斜率优化

　L公司有N个工厂，由高到底分布在一座山上。如图所示，工厂1在山顶，工厂N在山脚。由于这座山处于高原内
陆地区（干燥少雨），L公司一般把产品直接堆放在露天，以节省费用。突然有一天，L公司的总裁L先生接到气象
部门的电话，被告知三天之后将有一场暴雨，于是L先生决定紧急在某些工厂建立一些仓库以免产品被淋坏。由于
地形的不同，在不同工厂建立仓库的费用可能是不同的。第i个工厂目前已有成品Pi件，在第i个工厂位置建立仓库
的费用是Ci。对于没有建立仓库的工厂，其产品应被运往其他的仓库进行储藏，而由于L公司产品的对外销售处设
置在山脚的工厂N，故产品只能往山下运（即只能运往编号更大的工厂的仓库），当然运送产品也是需要费用的，
假设一件产品运送1个单位距离的费用是1。假设建立的仓库容量都都是足够大的，可以容下所有的产品。你将得到
以下数据：1：工厂i距离工厂1的距离Xi（其中X1=0）;2：工厂i目前已有成品数量Pi;:3：在工厂i建立仓库的费用
Ci;请你帮助L公司寻找一个仓库建设的方案，使得总的费用（建造费用+运输费用）最小。

Input

　　第一行包含一个整数N，表示工厂的个数。接下来N行每行包含两个整数Xi, Pi, Ci, 意义如题中所述。

Output

　　仅包含一个整数，为可以找到最优方案的费用。

Sample Input

3
0 5 10
5 3 100
9 6 10

Sample Output

32

Hint

　　在工厂1和工厂3建立仓库，建立费用为10+10=20，运输费用为(9-5)*3 = 12，总费用32。如果仅在工厂3建立仓库，建立费用为10，运输费用为(9-0)*5+(9-5)*3=57，总费用67，不如前者优。

【数据规模】

　　对于100%的数据， N ≤1000000。 所有的Xi, Pi, Ci均在32位带符号整数以内，保证中间计算结果不超过64位带符号整数。 

---

    题不是很难，dp方程推错了两次（每次都是从n往前），于是无限WA...第三次终于推对了。。（说完一堆废话赶快写正解）

　　朴素dp的方程（公式编辑器坏了，只能用画图了，请谅解）

$f\left [ i \right ] = \min\left \{ f\left [ j \right ] + \sum_{k = j + 1}^{i - 1}\left ( x_{i} - x_{k} \right )p_{k} \right \} + c_{i}$

　　一看是三维，死得没有悬念，只能想办法优化。Sigma一在更不好优化，只能先展开

    发现P的求和和xP的求和都是可以用前缀和搞定的，于是设，sump[i] = P₁ + P₂ + ... + P_i,sumxp[i] = x₁P₁ + x₂P₂ + ... + x_iP_i

    于是方程变成        f[i] = min{f[j] + x_i(sump[i - 1] - sump[j]) - sumxp[i - 1] + sump[j]} + C_i

    现在假设能转移到状态i的有两个状态j, k(j < k)，如果j比k优，那么

f[j] + x_i(sump[i - 1] - sump[j]) - sumxp[i - 1] + sump[j] < f[k] + x_i(sump[i - 1] - sump[k]) - sumxp[i - 1] + sump[k]

    拆括号化简

f[j] - x_isump[j] + sump[j] < f[k] - x_isump[k] + sump[k]

    右边保留和i有关的单项式

(f[j] + sump[j]) - (f[k] + sump[k]) < x_i(sump[j] - sump[k])

    移项(还是注意不等号的方向)

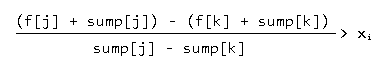
    于是又愉快地得到了斜率方程，对于状态i，(f[i] + sump[i])作为纵坐标,sump[i]作为横坐标，删掉上凸点，维护一条斜率递增的折线。

Code

/**
 * bzoj
 * Problem#1096
 * Accepted
 * Time:2312ms
 * Memory:36464k
 */
#include<iostream>
#include<sstream>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<queue>
#include<set>
#include<map>
#include<stack>
#include<vector>
#include<algorithm>
#ifdef    WIN32
#define    AUTO "%I64d"
#else
#define AUTO "%lld"
#endif
using namespace std;
typedef bool boolean;
#define smin(a, b) (a) = min((a), (b))
#define smax(a, b) (a) = max((a), (b))
template<typename T>
inline void readInteger(T& u){
    char x;
    int aFlag = 1;
    while(!isdigit((x = getchar())) && x != '-');
    if(x == '-'){
        aFlag = -1;
        x = getchar();
    }
    for(u = x - '0'; isdigit((x = getchar())); u = u * 10 + x - '0');
    ungetc(x, stdin);
    u *= aFlag;
}

template<typename T>
class IndexedDeque{
    public:
        T* list;
        int pfront;
        int prear;
        IndexedDeque():list(NULL), pfront(0), prear(0){        }
        IndexedDeque(int size):pfront(0), prear(0){
            list = new T[size];
        }
        void push_front(T x){    list[--pfront] = x;        }
        void push_back(T x)    {    list[prear++] = x;        }
        void pop_front()    {    ++pfront;                }
        void pop_back()        {    --prear;                }
        T     front()        {    return list[pfront];    }
        T     rear()            {    return list[prear - 1];        }
        T& operator [](int pos){            return list[pfront + pos];        }
        int size()            {    return prear - pfront;    }
};

template<typename T>
inline void aalloc(T*& array, int size){    array = new T[(const int)(size + 1)];    }

int n;
long long* sump;
long long* sumxp;
int* c;
int* x;
long long* f;
IndexedDeque<int> que;

long long y_pos(int i)    {    return f[i] + sumxp[i];    }
double slope(int j, int k)    {    return (y_pos(j) - y_pos(k)) * 1.0 / (sump[j] - sump[k]);    }
double cmpSlope(int i, int j, int k) {    return slope(j, k) - x[i];    }    

inline void init() {
    readInteger(n);
    aalloc(sump, n);
    aalloc(sumxp, n);
    aalloc(c, n);
    aalloc(x, n);
    aalloc(f, n + 1);
    sump[0] = sumxp[0] = x[0] = 0;
    for(int i = 1, p; i <= n; i++){
        readInteger(x[i]);
        readInteger(p);
        readInteger(c[i]);
        sump[i] = sump[i - 1] + p;
        sumxp[i] = sumxp[i - 1] + x[i] * 1LL * p;
    }
}

inline void solve() {
    que = IndexedDeque<int>(n + 5);
    f[0] = 0;
    que.push_back(0);
    for(int i = 1; i <= n; i++) {
        while(que.size() > 1 && cmpSlope(i, que[0], que[1]) < 0)    que.pop_front();
        int j = que.front();
        f[i] = f[j] + x[i] * (sump[i - 1] - sump[j]) - sumxp[i - 1] + sumxp[j] + c[i];
        while(que.size() > 1 && slope(que[que.size() - 2], que[que.size() - 1]) >= slope(que[que.size() - 1], i))    que.pop_back();
        que.push_back(i);
    }
    printf(AUTO"\n", f[n]);
}

int main() {
    init();
    solve();
    return 0;
}