（普通的)莫队算法简单介绍

　　莫队算法（由莫涛发明的）是一种离线的暴力算法（至少我这么认为）。使用莫队算法的条件是，知道一个区间[l, r]的结果，那么也可以快速知道[l + 1, r],[l - 1, r], [l, r - 1], [l, r + 1]这四个区间的结果。于是可以想到，直接通过这样转移来解决一些问题。当然有些出题人机智，故意卡这种暴力，让你从头跑到尾然后从尾跑到头，于是时间复杂度高达O(n²)

　　而莫队算法就是通过改变处理询问的顺序来降低时间复杂度。

　　比如说现在知道一个区间[l1, r1]，又要转移到[l2, r2]，那么它的所要付出的代价将是O((∣l1 - l2∣+∣r1 - r2∣)*a)(a为每次转移的时间复杂度),如果知道曼哈顿距离公式就会发现似乎长得很像。于是就可以把它抽象成二维中的点，于是便可以用曼哈顿距离最小生成树来完成排序。

　　但是呢，这玩意儿过于复杂（亲看见别人写上298行，估计自己会写上300行），而且不是很常用，于是就用分块来代替曼哈顿距离最小生成树。

　　每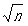个元素分为一块。读入所有的询问，为每个询问的l除以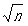的结果取整（向下取整还是向上取整随意，只要不自己坑自己就行了）的结果作为第一关键字，r作为第二关键字，从小到大进行排序。

　　然后每次处理第i块内的所有询问（从上一个询问跑回来或者从头开始跑）一共会处理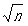块，处理一块的时间复杂度是O(an)，所以总时间复杂度O(an^1.5)。

　　关于处理一块的时间复杂度是O(an)懂一点点，把区间的l,r分开看，假设l被坑得很惨，左右到处乱跑，最多会跑不超过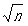*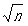=n次，因为r是有序，所以会移动不超过n次，于是总移动次数不超过2n，再乘上每次移动的代价，2就隐藏在大O标记下。

　　推荐一道例题 bzoj 2038 小Z的袜子