bzoj 2038 A-小Z的袜子[hose] - 莫队算法
作为一个生活散漫的人，小Z每天早上都要耗费很久从一堆五颜六色的袜子中找出一双来穿。终于有一天，小Z再也无法忍受这恼人的找袜子过程，于是他决定听天由命……
具体来说，小Z把这N只袜子从1到N编号，然后从编号L到R(L 尽管小Z并不在意两只袜子是不是完整的一双，甚至不在意两只袜子是否一左一右，他却很在意袜子的颜色，毕竟穿两只不同色的袜子会很尴尬。
你的任务便是告诉小Z，他有多大的概率抽到两只颜色相同的袜子。当然，小Z希望这个概率尽量高，所以他可能会询问多个(L,R)以方便自己选择。
Input
输入文件第一行包含两个正整数N和M。N为袜子的数量，M为小Z所提的询问的数量。接下来一行包含N个正整数Ci，其中Ci表示第i只袜子的颜色，相同的颜色用相同的数字表示。再接下来M行，每行两个正整数L，R表示一个询问。
Output
包含M行，对于每个询问在一行中输出分数A/B表示从该询问的区间[L,R]中随机抽出两只袜子颜色相同的概率。若该概率为0则输出0/1，否则输出的A/B必须为最简分数。（详见样例）
Sample Input
6 4 1 2 3 3 3 2 2 6 1 3 3 5 1 6
Sample Output
2/5 0/1 1/1 4/15 【样例解释】 询问1：共C(5,2)=10种可能，其中抽出两个2有1种可能，抽出两个3有3种可能，概率为(1+3)/10=4/10=2/5。 询问2：共C(3,2)=3种可能，无法抽到颜色相同的袜子，概率为0/3=0/1。 询问3：共C(3,2)=3种可能，均为抽出两个3，概率为3/3=1/1。 注：上述C(a, b)表示组合数，组合数C(a, b)等价于在a个不同的物品中选取b个的选取方案数。 【数据规模和约定】 30%的数据中 N,M ≤ 5000； 60%的数据中 N,M ≤ 25000； 100%的数据中 N,M ≤ 50000，1 ≤ L < R ≤ N，Ci ≤ N。
这个是支持离线的一道题，那么可以试试用莫队算法。
那么看能不能在已知一个区间[l, r]的情况下，快速知道[l - 1, r],[l +１, r],[l, r - 1]和[l, r + 1]。这列主要最难(其实也不难)找的是方案数。那么来看，如果某种袜子现有x个，那么新加同一种袜子增加的方案数为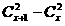
。然后再展开:
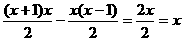
删除同理。
Code
1 /** 2 * bzoj 3 * Problem2038 4 * Accepted 5 * Time:820ms 6 * Memory:3264k 7 */ 8 #include<iostream> 9 #include<fstream> 10 #include<sstream> 11 #include<cstdio> 12 #include<cstdlib> 13 #include<cstring> 14 #include<ctime> 15 #include<cctype> 16 #include<cmath> 17 #include<algorithm> 18 #include<stack> 19 #include<queue> 20 #include<set> 21 #include<map> 22 #include<vector> 23 using namespace std; 24 typedef bool boolean; 25 #define smin(a, b) (a) = min((a), (b)) 26 #define smax(a, b) (a) = max((a), (b)) 27 template<typename T> 28 inline void readInteger(T& u){ 29 char x; 30 int aFlag = 1; 31 while(!isdigit((x = getchar())) && x != '-' && x != -1); 32 if(x == -1) return; 33 if(x == '-'){ 34 x = getchar(); 35 aFlag = -1; 36 } 37 for(u = x - '0'; isdigit((x = getchar())); u = (u << 3) + (u << 1) + x - '0'); 38 ungetc(x, stdin); 39 u *= aFlag; 40 } 41 42 typedef class Segment{ 43 public: 44 int from; 45 int end; 46 int id; 47 int index; 48 Segment():from(0), end(0), index(0){ } 49 boolean operator < (Segment another) const{ 50 if(this->id != another.id) return this->id < another.id; 51 return this->end < another.end; 52 } 53 }Segment; 54 55 int n, m; 56 Segment* seg; 57 int *colors; 58 int divs; 59 int blocks; 60 61 inline long long C(int x){ 62 return (x * 1LL * (x - 1) / 2); 63 } 64 65 template<typename T> 66 inline T gcd(T a, T b){ 67 if(b == 0) return a; 68 return gcd(b, a % b); 69 } 70 71 inline void init(){ 72 readInteger(n); 73 readInteger(m); 74 seg = new Segment[(const int)(m + 1)]; 75 colors = new int[(const int)(n + 1)]; 76 divs = (int)(sqrt(n + 0.5)); 77 blocks = n / divs + (n % divs == 0) ? (1) : (0); 78 for(int i = 1; i <= n; i++){ 79 readInteger(colors[i]); 80 } 81 for(int i = 1; i <= m; i++){ 82 readInteger(seg[i].from); 83 readInteger(seg[i].end); 84 seg[i].index = i; 85 seg[i].id = seg[i].from / divs; 86 } 87 } 88 89 int* ccolor; 90 long long *resa, *resb; 91 92 inline void solve(){ 93 sort(seg + 1, seg + m + 1); 94 ccolor = new int[(const int)(n + 1)]; 95 resa = new long long[(const int)(m + 1)]; 96 resb = new long long[(const int)(m + 1)]; 97 int pseg = 1; 98 99 int mdzzf = 1, mdzzr = 1; //莫队指针，左闭右开 100 long long qk = 0; 101 memset(ccolor, 0, sizeof(int) * (n + 1)); 102 for(int i = 1; i <= m; i++){ 103 if(seg[i].from == seg[i].end){ 104 resa[seg[i].index] = 0; 105 continue; 106 } 107 while(mdzzr > seg[pseg].end + 1) qk -= --ccolor[colors[--mdzzr]]; 108 while(mdzzf > seg[pseg].from) qk += ccolor[colors[--mdzzf]]++; 109 while(mdzzr <= seg[pseg].end) qk += ccolor[colors[mdzzr++]]++; 110 while(mdzzf < seg[pseg].from) qk -= --ccolor[colors[mdzzf++]]; 111 resa[seg[pseg].index] = qk; 112 resb[seg[pseg].index] = C(seg[pseg].end - seg[pseg].from + 1); 113 pseg++; 114 } 115 for(int i = 1; i <= m; i++){ 116 if(resa[i] == 0){ 117 printf("0/1\n"); 118 continue; 119 } 120 long long g = gcd(resa[i], resb[i]); 121 printf("%lld/%lld\n", resa[i] / g, resb[i] / g); 122 } 123 } 124 125 int main(){ 126 init(); 127 solve(); 128 return 0; 129 }
