某模拟题题解 2016.11.15

---

　　二叉树是一个幌子，其实中序遍历后变成数列。

　　原问题变成了给定一个数列，问最少把多少个数修改为其他整数，使得数列递增。

　　考察修改后要满足的条件（$b$数组为中序遍历后得到的数组），即

$b_{i}\leqslant b_{i + 1} - 1$

　　所以有：

$b_{i} - i\leqslant b_{i + 1} -\left ( i + 1  \right )$

　　设$c_{i} = b_{i} - i$，那么求它的最长不下降子序列的长度就是不用修改的数的个数的最大值，用$n$减去它即可得到答案。

Code

#include<iostream>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<fstream>
#include<sstream>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<vector>
#include<stack>
using namespace std;
typedef bool boolean;
#define INF 0xfffffff
#define smin(a, b) a = min(a, b)
#define smax(a, b) a = max(a, b)
template<typename T>
inline void readInteger(T& u){
    char x;
    int aFlag = 1;
    while(!isdigit((x = getchar())) && x != '-');
    if(x == '-'){
        x = getchar();
        aFlag = -1;
    }
    for(u = x - '0'; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - '0');
    ungetc(x, stdin);
    u *= aFlag;
}

typedef class TreeNode{
    public:
        int next[2];
        int val;
        TreeNode(){
            next[0] = next[1] = 0; 
        }
}TreeNode;

template<typename T>
class IndexedStack{
    public:
        T *p;
        int s;
        IndexedStack():s(0), p(NULL){    }
        IndexedStack(int size):s(0){
            p = new T[(const int)size];
        }
        boolean empty()        {    return s == 0;            }
        T top()            {    return p[s - 1];        }
        void pop()        {    s--;                }
        void push(T& x)        {    p[s++] = x;            }
        void clear()        {    s = 0;                }
        int size()        {    return s;                }
        T& operator [](int pos)    {    return p[pos];            }
};

inline int lower_bound(int* a, int from, int end, int val){
    int l = from, r = end - 1;
    while(l <= r){
        int mid = (l + r) >> 1;
        if(a[mid] > val)    r = mid - 1;
        else l = mid + 1;
    }
    return r + 1;
}

int n;
int *a;
TreeNode* tree;

inline void init(){
    readInteger(n);
    tree = new TreeNode[(const int)(n + 1)];
    for(int i = 1; i <= n; i++){
        readInteger(tree[i].val);
    }
    for(int i = 2, a, b; i <= n; i++){
        readInteger(a);
        readInteger(b);
        tree[a].next[b] = i;
    }
}

IndexedStack<int> s;
inline int lis(){
    s = IndexedStack<int>(n);
    for(int i = 1; i <= n; i++){
        if(s.empty() || a[i] >= s.top()){
            s.push(a[i]);
        }else{
            int x = lower_bound(s.p, 0, s.size(), a[i]);
            s[x] = a[i];
        }
    }
    return s.size();
}

int cv;
void inorder(int node){
    if(tree[node].next[0])    inorder(tree[node].next[0]);
    a[++cv] = tree[node].val - cv;
    if(tree[node].next[1])    inorder(tree[node].next[1]);
}

inline void solve(){
    a = new int[(const int)(n + 1)];
    inorder(1);
    int l = lis();
    printf("%d", n - l);
}

int main(){
    freopen("tree.in", "r", stdin);
    freopen("tree.out", "w", stdout);
    init();
    solve();
    return 0;
}

 

---

---

    这道题算是一道很神奇的数论题吧。可以转化成图论（模最小的长度，然后跑最短路）来做，只不过有一个比较简单的方法,重点在于如何判断
    大概分为下面三种情况

1. 当所有的长度的最大公约数不为1时，一定不存在最大的不能修建的长度
2. 当最小的一段为1时，也不存在（因为就没有不能围成的长度（len > 0）（如果木头足够的话））
3. 当有一段长度为最小的那一段的长度都是可以围成的，那么刚刚找到的最大的不能的就是所求答案

Code

#include<iostream>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<fstream>
#include<sstream>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<vector>
#include<stack>
using namespace std;
typedef bool boolean;
#define INF 0xfffffff
#define smin(a, b) a = min(a, b)
#define smax(a, b) a = max(a, b)
template<typename T>
inline void readInteger(T& u){
    char x;
    int aFlag = 1;
    while(!isdigit((x = getchar())) && x != '-');
    if(x == '-'){
        x = getchar();
        aFlag = -1;
    }
    for(u = x - '0'; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - '0');
    ungetc(x, stdin);
    u *= aFlag;
}

template<typename T>
T gcd(T a, T b){
    if(b == 0)    return a;
    return gcd(b, a % b);
}

int n, m;
int *a;
int cl;
boolean visited[3001];
boolean f[5000000];
int lis[3001];

inline void init(){
    readInteger(n);
    readInteger(m);
    a = new int[(const int)(n + 1)];
    for(int i = 1; i <= n; i++){
        readInteger(a[i]);
    }
}

inline void getList(){
    for(int i = 1; i <= n; i++){
        int j = m;
        visited[a[i]] = true;
        while(j && a[i]){
            visited[--a[i]] = true;
            j--;
        }
    }
    for(int i = 1; i <= 3000; i++){
        if(visited[i]){
            lis[++cl] = i;
        }
    }
}

inline void solve(){
    if(lis[1] == 1){
        printf("-1");
        return;
    }
    int temp = lis[1];
    for(int i = 2; i <= cl; i++)
        temp = gcd(temp, lis[i]);
    if(temp != 1){
        printf("-1");
        return;
    }
    f[0] = true;
    int last = 0;
    int maxv = -1;
    for(int i = 1; i < 5000000; i++){
        for(int j = 1; j <= cl; j++){
            if(lis[j] > i)    continue;
            if(f[i - lis[j]]){
                f[i] = true;
                break;
            }
        }
        if(!f[i]){
            last = 0;
            maxv = i;
        }else last++;
        if(last == lis[1]){
            printf("%d", maxv);
            return;
        }
    }
    printf("-1");
}

int main(){
    freopen("bullpen.in", "r", stdin);
    freopen("bullpen.out", "w", stdout);
    init();
    getList();
    solve();
    return 0;
}

---

---

    仔细分析一下，很快你就会推出一个式子

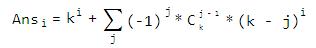
再拿几个展开式来看看，对照着看，然后再一列一列地看，你会高兴地发现这是一个等比数列

Code

#include<iostream>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<fstream>
#include<sstream>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<vector>
#include<stack>
using namespace std;
typedef bool boolean;
#define INF 0xfffffff
#define smin(a, b) a = min(a, b)
#define smax(a, b) a = max(a, b)
template<typename T>
inline void readInteger(T& u){
    char x;
    int aFlag = 1;
    while(!isdigit((x = getchar())) && x != '-');
    if(x == '-'){
        x = getchar();
        aFlag = -1;
    }
    for(u = x - '0'; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - '0');
    ungetc(x, stdin);
    u *= aFlag;
}

template<typename T>
inline void putInteger(T u){
    if(u == 0){
        putchar('0');
        return;
    }
    if(u < 0){
        putchar('-');
        u *= -1;
    }
    stack<char>    s;
    while(u != 0)    s.push(u % 10 + '0'), u /= 10;
    while(!s.empty())    putchar(s.top()), s.pop();
}

const int moder = 1234567891;

long long _pow(long long x, int pos){
    if(x == 1)    return 1;
    if(pos == 1)    return x;
    long long temp = _pow(x, pos / 2);
    if(pos & 1)    return    temp * temp % moder * x % moder;
    return temp * temp % moder;
}

int T;
int n, k;

long long C[32][32];

inline void init_c(){
    C[0][0] = 1;
    for(int i = 1; i <= 31; i++){
        for(int j = 1; j <= i; j++){
            C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
        }
    }
}

inline void init(){
    readInteger(n);
    readInteger(k);
}

inline void solve(){
    int sign = 1;
    long long result = 0, inv;
    for(int i = k; i >= 1; i--){
        long long a1 = i;
        long long an = _pow(i, n);
        if(i == 1){            //最后一项 
            (result += sign * ((n * C[k + 1][k]) % moder) + moder) %= moder;
        }else{
            inv = _pow(i - 1, moder - 2);
            (result += sign * ((an * i % moder - a1 + moder) % moder * inv % moder * C[k + 1][k - i + 1]) + moder) %= moder;
        }
        sign *= -1;
    }
    putInteger(result);
    putchar('\n');
}

int main(){
    freopen("pearl.in", "r", stdin);
    freopen("pearl.out", "w", stdout);
    init_c();
    readInteger(T);
    while(T--){
        init();
        solve();
    }
    return 0;
}